Download Functional Programming with Lists

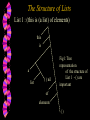
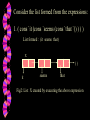
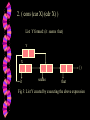
CS535
Programming Languages
Chapter - 10
Functional Programming
With Lists
Outline
• Functional Language: LISP
• Scheme, a Dialect of LISP
• The structure of lists
• List manipulation
• Storage allocation for lists
Functional Language: LISP
• Includes all the basic concepts of
functional programming
• First designed in 1958 by John McCarthy
• Functions include recursion, first-class
functions and garbage collection
• Lisp implementation led the way in
integrated programming environments
Scheme, A Dialect Of LISP

A scheme is a small language that provides
constructs at the core of Lisp

Constructs include:
1. Conditionals
2. The “ let ” construct
3. Quoting (data in the form of expressions)
Expression




Scheme uses a form of prefix notation for
expressions
The general form of an expression in
Scheme is
( E1 E2 E3 …… Eη)
The expression 4 + 5 * 7 is written as
( + 4 (* 5 7) )
The above uniformity in Lisp syntax makes
it easy to manipulate programs as data
Function Definition

The recursive and non recursive function
definition associates a function value
with a name

The general syntax of function definition:
( define (<function name> <arguments>) <expression>

An example:
( define ( Square X ) ( * X X ) )
; (Square 5) = 25
Conditionals

Conditional expressions come in two forms
1. (if P E1 E2)
2. ( cond ( P1 E1) ….
( Pn E n )
( else E n + 1 ) )

Conditionals are generally required for
recursive functions
let Construct

The general syntax of the let construct is
( let ( (X1 E1 ) (X 2 E 2) … (X k E k) ) F )

For instance (3*3) + (4*4) is written as
(
let ( (three-sq(square 3))
(four-sq(square 4) )
(+ three -sq four-sq)
25
)
Quoting


Used to choose a spelling as a symbol or a
variable name
Two methods of quoting are:
1. ( quote <item> )
2. `<item>

( define f * )
(f 2 3)

( define f `* ) //Quoted represents symbol which is a bad
procedure
(f 2 3)
// Unquoted
6
The Structure of Lists
List 1 : (this is (a list) of elements)
this
is
a
list
( ) nil
Fig1: Tree
representation
of the structure of
List 1 - () are
important
of
elements
()
Operations on Lists
List X: ()
List Y: ( this is (a list) of elements)
Basic Operation
Result
1. (null? X)
# t (rue)
2. ( car Y )
this (first element)
3. ( cdr X )
(is (a list) of elements)
(rest of the list after the first is removed)
4. (car (cdr X) )
5. (cdr (cdr X) )
6. (cons a X )
is
( (a list) of elements )
(a)
List Manipulation
1. Length function:
The equation for non empty list X :
(length x) = (+ 1 (length (cdr x) ) )
Corresponding length function definition:
( define (length X)
(
)
)
cond ( (null? X) 0)
(else (+ 1 ( length (cdr x) ) )
2. Append function:
The equation for appending two lists is:
(append X Z) = (cons (car X) (append (cdr X) Z))
Corresponding append function definition:
(define (append X Z)
( cond ( ( null? X) Z)
(else (cons (car X) (append (cdr X) Z) ) )
)
)
3. Mapping a function
A function f applied to a single list element
can be extended using map and applied to all
elements of the same list
Eg: Considering the square function ,
( define (square n) (* n n ) )
( map square `( 1 2 3 4 5 ) )
Result : (1 4 9 16 25)
Storage allocation for lists
• Implementation of lists in Scheme and ML
is usually done by using cells.
•Each cell holds pointers to the head and tail
or car and cdr, respectively
• The cons operation allocates a single cell
• Each execution of cons returns a pointer to
a newly allocated cell
Consider the list formed from the expressions:
1. ( cons `it (cons `seems (cons `that `() ) ) )
List formed : (it seems that)
X
()
it
seems
that
Fig2: List X created by executing the above expression
2. ( cons (car X) (cdr X) )
List Y formed: (it seems that)
Y
X
()
it
seems
that
Fig 3: List Y created by executing the above expression
Allocation and Deallocation

Cells no longer in use have to be deallocated
to avoid the problems of memory shortage
 A standard technique is to link the cells on a
list called a free list
 A free list acts as a stack of cells on which the
standard PUSH and POP operations are
performed
 A language implementation performs the
garbage collection when it returns cells to the
free list
Approaches to Deallocation of cells
1. Lazy approach:
• Deallocation starts only after all the memory
is exhausted, after which all the dead cells are
collected.
• This method is time consuming
• Possibility of interrupting the ongoing
processing
2. Eager approach:
• Deallocating is done by checking a cell
for any future requirement in an operation
• The cell is then placed on the free list to be freshly
allocated on a POP operation
• Standard technique is to reserve some space
in each cell for a reference count of the number
of pointers to the cell.
Implementation of garbage collection

The Mark Sweep Approach:
1. Mark phase involves marking all the cells which
can be reached by following pointers.
2. Sweep phase involves sweeping through the
memory, looking for any unmarked cells.
3. The sweeping phase starts at one end of the
memory and looks at every cell
4. Once identified, all the unmarked cells are sent
to the free list for fresh allocation.
Equal? And Eq?


Equal? - value equality
eq? - pointer equality