* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Engineering Science EAB_S_127_Ch3
Josephson voltage standard wikipedia , lookup
Operational amplifier wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Power electronics wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Integrating ADC wikipedia , lookup
Current source wikipedia , lookup
Current mirror wikipedia , lookup
Oscilloscope history wikipedia , lookup
Opto-isolator wikipedia , lookup
Surge protector wikipedia , lookup
Power MOSFET wikipedia , lookup
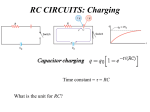
Engineering Science EAB_S_127 Electricity Chapter 3 & 4 Overview Measurement of electrical resistance The Wheatstone Bridge Capacitance Energy stored in a capacitor Charging and Discharging through a resistor Time constants The Wheatstone Bridge We use an “Ohmmeter” to measure an unknown resistance The heart of the simplest Ohmmeter is a so-called “Wheatstone Bridge” circuit If R1 was a variable resistor, we can adjust it until Vab = 0 The Balanced Wheatstone Bridge When Vab = 0, a special condition occurs: the bridge is said to be “balanced”, i.e. Va = Vb This implies that ig = 0, hence from KCL, i4 = i3 and i2 = i1 Further, from Ohm’s Law; i4R4 = i2R2 and i3R3 = i1R1 The Wheatstone Bridge continued Hence i1 R1 i3 R3 i2 R2 i4 R4 R3 R1 R2 R4 The Wheatstone Bridge: Example Calculate R1 in a Wheatstone bridge when it is balanced and when R2 = 300Ω, R3 = 200Ω, R4 = 100Ω . R3 R1 R2 R4 Answer: R3 200 R1 R2 300 600 R4 100 Unbalanced Wheatstone Bridge The following unbalanced Wheatstone Bridge is constructed. Calculate the output voltage across points C and D For the first series arm, ACB The voltage across points C-D is given as For the second series arm, ADB Capacitors Type of Capacitors Applications of capacitors Energy storage Pulsed power and weapons Power conditioning Motor starters Signal processing Capacitance Capacitors are devices which store electrical charge A capacitor consists of two plates separated by an insulator, as shown in Figure 4.1 The negative plate is connected to a low potential and the positive plate to a high potential Insulator Q - + - + - + V Negative plate Figure 4.1 Positive plate Capacitance continued The total amount of the charge stored, is denoted by Q and the voltage across the plates by V Q The capacitance then is defined as C [F ] V Where C is in Farads 1 Farad = 1 Coulomb per Volt 1mF, µF, nF (nano), pF(pico) 0.1 pF is the smallest available in capacitors Insulator Q for general use in electronic design + - + - + V Negative plate Figure 4.1 Positive plate Energy Stored in a Capacitor When charged, a capacitor stores electrical energy Recall the formula for electrical energy in a circuit, which is W = VQ However, we need to be careful as the voltage between the plates in a capacitor varies from 0 to V Hence, to be more accurate we should use the average 0 Vab Vab voltage Vm W VmQ So Hence W Vab Q 2 2 2 and we know Vab 1 CVab CVab2 2 2 Q CVab Energy Stored in a Capacitor: Example Question: A capacitor is supplied with 10 V in a circuit. If its capacitance is 150µF, what is the electrical energy stored in the capacitor? Answer: W 1 1 CVab2 150 10 6 10 2 75 10 4 J 7.5mJ 2 2 Charging and discharging a capacitor Charging and discharging a capacitor Charging and Discharging a Capacitor Charging and discharging a capacitor from a DC (direct current) source is shown below V We assume that the voltage source,V, has no internal resistance If the switch was held in position 2 for a long time, then the capacitor would be completely discharged, Vc = 0V Charging a Capacitor If the switch is then moved to position 1, current will start to flow through the resistor R, thereby charging the capacitor, C The voltage across the plates of the capacitor will rise in time, until after a long time, the capacitor will have the same voltage as the supply,V V VC Discharging a Capacitor If the switch is then moved back to position 2, current will start to flow through the resistor R, thereby discharging the capacitor, C The voltage across the plates of the capacitor will fall in time, until after a long time, the capacitor will have no charge at all and again, Vc = 0V V VC Time Constant of an RC Circuit It can be shown mathematically, that the time for the voltage to fall to 37% of its original voltage, t = RC The charging and discharging curves have an exponential nature When discharging V C When charging V C RC Time Constant: Example Question: If R = 1000 and C = 0.1mF, what is the time constant of the circuit? Answer: t = RC = 1000x0.1x10-6 = 0.1 x10-3 = 100ms Hence, when discharging, the following equation can be used to calculate the voltage When charging Summary Learning Outcomes: Wheatstone Bridge Balanced Condition Capacitors and capacitance Energy stored in a capacitor Charging a capacitor Time constants Exponential charging and discharging curves