Download Revision - Electromagnetic Induction Explained File

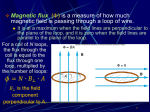
Magnet Fields
5.14 Magnetic Flux.
5.15 Electromagnetic Induction
5.16 Magnetic Effect of a Steady Current
Home
5.14 Magnetic Flux



Magnetic flux
flux linkage.
 = BA
Home
Magnetic Flux



The magnetic flux is a measure of the number
of field lines passing through a region.
The unit of magnetic flux is the weber (Wb)
It is a vector quantity
A
A uniform
magnetic
field has a
constant
density of
field lines
throughout
B
In a uniform field
the number of field
lines passing through
the larger region B is
greater than through
the smaller region A.
Therefore we can
say that there is a
greater flux through
B than A
Home
Magnetic Flux
Here the magnetic flux is
the same in region A and B.
Sometimes a measure of
magnetic flux can be
misleading.
Home
Magnetic Flux

Below the magnetic flux through region A is
greater than through B because the density of
the field lines is greater.
A
B
Home
Magnetic flux density




The magnetic flux density is represented by
the symbol B.
It is measured in Tesla (T).
It is a measure of the flux per square metre.
This enables us to compare the field strength
Home
Magnetic Flux







Definition:
 Magnetic field lines are lines of magnetic flux.
 The product between the magnetic flux density and
the area when the field is at right angles to the area.
 The area can be thought of as the area swept out by a
conductor.
Symbol: 
Equation:  = BA
Units: Wb (Weber) or Tm2
Note:
The magnetic field strength is also known as the Magnetic
Flux Density.
Magnetic Flux Density = Magnetic Flux
Area
thus Magnetic Flux = Magnetic Flux Density x area
Home
Magnetic Flux Linkage

When we are dealing with stationary
conductors in changing magnetic fields, we
often work with loops and coils of wires.
Home


Simply treat each loop of the coil as if it was
on its own. Hence, if you have 'n' loops in the
coil you have 'n' times the area and therefore
'n' times the flux.
This is called flux linkage, F.
Home
Flux Linkage

If each turn cuts (or links) flux , the total flux
linkage for N turns must be N .

We can also write this as NBA.

Flux linkage = number of turns of wire x magnetic field strength x area



The flux linkage can be changed in two ways:
We can alter the strength of the magnetic field;
We can alter the area at 90° to the magnetic field
by moving the coil.
Home
Electromagnetic Induction







Experimental demonstration that change of flux
induces an e.m.f. in a circuit.
 Data logging: V against t as a magnet falls through
coil.
Faraday’s and Lenz’s laws of electromagnetic induction.
e.m.f. as equal to rate of change of magnetic flux
linkage.
Lenz’s law as illustrating energy conservation.
 = N/t
Investigations:
Faraday’s law - variation of with N and rate of change
of B.
Home
Inducing a Voltage: Moving Conductor

As you swipe the metal bar to the left you sweep
through the area of field shown by the crosses.
• It’s this movement through a field that induces
(produces) an e.m.f. across the bar ends.
Home
Increasing the Induced EMF



A longer bar would ‘sweep’ out more area of
field.
A stronger field would mean you swept through
more field lines when moving the same distance.
A faster swipe would mean you swept out more
area of the field per second.
Home
Method 2: Changing the Field


Changing the Magnetic Field Around a Conductor.
i.e. moving a magnet in a coil.
Increasing the Induced EMF:
 More turns
 Stronger field
 Quicker changing field
Home
Faraday’s law




Used to find magnitude of induced emf
“an induced emf is directly proportional to
rate of change of flux linkage or flux
cutting”
i.e.   - d(N)
dt
i.e. to increase the e.m.f. you can:
 increase the number of turns
 the amount of flux through the coil
 the rate of change of the flux (speed of
magnet or change of magnetic field)
Home
Experimental Proof of Faraday’s Law



Investigate changing frequency and number of
turns on second coil on induced emf
Conclusions:
Increase frequency or Number turns on secondary coil
increases the induced EMF
Home



Definition of Weber:
the magnetic flux that induces in a 1 turn coil
an emf of 1 volt when the flux is reduced to
zero in 1 second
Hence constant of proportionality = 1
 = - N d
dt
or
 = -N 
t
Home
Demo

Hovering Aluminium Ring
Home
Lenz’s law




The direction of any induced current is such as
to oppose the flux change that caused it
i.e. if you induce a current it will create a
magnetic field to oppose the motion that made
it – otherwise you would be getting energy for
free!
Used to find direction of induced e.m.f.
This e.m.f. is often called the back e.m.f as it
opposes any flowing e.m.f. on a coil (e.g. a
motor)
Home
Effects of Lenz’s Law

Demo: Aluminium Ring through a magnet.

What will happen?

Why does it not work in both rings?

Demo: Magnet down Cu or Al pipe
Home
Right hand rule
Home
Remember


LEFT hand for motor effect of a magnetic field
RIGHT hand for generator effect (induced magnetic
field)
Home
The Transformer



The transformer. Explained in terms of
magnetic flux linkage.
For an ideal transformer: Vp/Vs = Np/Ns
Investigation: number of turns and output
voltage.
Home
Theory


A.C. in a coil will set
up a changing
magnetic field in the
coil, which will mean
that the core
becomes a constantly
changing magnet.
Put a second coil
around this changing
magnet (the core) and
you induce an
alternating e.m.f. in
the coil.
Home
Transformers
• We name the
first coil the
primary coil and
the second coil
the secondary
coil.
• If you change the number of turns in the coils you
change the induced emf.
• This allows you to change (transform) the voltage
from the primary to the secondary coil.
Home
Turns Rule
Ns = Vs
Np
Vp



Where:
 Ns = number of turns on the secondary coil
 Np = number of turns on the primary coil
 Vs = voltage across the secondary coil
 Vp = voltage across the primary coil
So if number of turns on the secondary coil is greater
than on the primary coil, the output voltage will be
greater than the input voltage.
This is called a step up transformer.
Home
Why Transform the Voltage
To deliver 10kW at 100V, the current needed is:
P = IV
I = P ÷ V
I = 10000 ÷ 100
= 100A
What is the effect of 100A travelling through a copper
wire?
P = I2R
= 1002 X 100
= 1 MW
Thus to supply 10 kW of power you waste 1 MW as heat
Home
Raising the Voltage
If we increase the voltage to 10 kV during
transmission, the current needed is:
P = IV
I = P ÷ V
I = 10000 ÷ 10000
= 1A
What is the effect of 1A travelling through a copper
wire?
P = I2R
= 12 X 100
= 0.1 kW
Thus to supply 10 kW of power you waste 100 W as heat
Home
Efficiency of Transformers





Transformers, however, are not 100 %
efficient.
Energy is lost in the wires in the coils and in
the iron core itself.
You can notice this with transformers in the
home – on your mobile charger for instance.
Small eddy currents are induced in the iron
core, which waste energy heating up the core.
Eddy currents can be reduced by laminating
the core - for instance, by making the core out
of thin slices of metal, which are ‘glued’
together.
Home
Electromagnetic induction
13.4.4
Home
13.4.2 force on a charge
Home
Home
Home
Applications
Home