Download Week 3, Lecture 1, Assigning probabilities to events

1
Business Statistics - QBM117
Assigning probabilities to events
Objectives

To define probability;

To describe the relationship between randomness and
probability;

To define a random experiment;

To revise the methods of assigning probabilities;

To introduce some of the probability rules.
2
What is probability?

Probability is a numerical measure of uncertainty;

It is a number that conveys the strength of our belief in the
occurrence of an uncertain event;

It is often associated with gambling;

It is now an indispensable tool in the analysis of situations
which involve uncertainty.
3
Randomness

What is the mean age of all the students in this class?

From a random sample of 10 students we can estimate the
mean age of all the students.

How can the mean, based on only a sample of 10, be an
accurate estimate of the population mean, ?

A second random sample would most likely produce a
different value for the mean.
4

This is due to sampling variability.

Why is this not a problem?

Chance behaviour is unpredictable in the short term but has
a regular and predictable pattern in the long term.

For example, consider the experiment of tossing a coin

The results cannot be predicted in advance but there is a
pattern which emerges, only after repeated sampling.

This is the basis for probability.
5
Randomness and probability

A phenomenon is called random if the individual
outcomes are uncertain, but there is a regular distribution
of outcomes in a large number of repetitions.

The probability of any outcome of a random phenomenon
is the proportion of times the outcome would occur in a
very long series of repetitions.
Probability is an idealisation based on what would
happen in an infinitely long series of trials.
6
Random experiments
We begin our study of probability by considering the
random experiment, as this process generates the
uncertain outcomes to which we assign probabilities.
A random experiment is any well defined procedure
that results in one of a number of possible outcomes.
The outcome that occurs, cannot be predicted with
certainty.
For example, rolling a die and observing the number
uppermost on the die.
7
Important

The actual outcome of a random experiment cannot be
determined in advance.

We can only talk about the probability that a particular
outcome will occur.
8
The sample space
is the complete list of all the possible outcomes of an
experiment.
Example
If we roll a die, the uppermost face can be a
1, 2, 3, 4, 5 or a 6. These numbers form the
sample space.
5
1
2
3
4
6
Sample Space
9
Events
The desired outcome or outcomes from the sample space.
Example
Rolling a die with an even number
uppermost can be an event.
Sample Space
1
3
5
2
4
6
10
Example
In a family of two children the
event of there being at least
one boy is:
Sample Space
girl / girl
boy / boy
girl / boy
boy / girl
11
Notation
Events can be described in written form, provided the
label is defined before hand.
Example
If we roll a die the uppermost face can be
either a 1, 2, 3, 4, 5 or a 6.
These numbers form the sample space.
The sample space can be written as:
S   1, 2, 3, 4, 5, 6 
12
Example
When rolling a die, let A
equal the even numbers.
A   2, 4, 6 
When rolling a die, let B
equal the numbers less than three.
B  1, 2 
13
Probability of an event
The probability of an event is defined as the number
of members in an event divided by the number of
members in the sample space.
n A 
P A  
n S 
Where n(A) is the number of members in the event A
and n (S ) is the number of members in the sample
space.
14
Example
When rolling a die:
S   1, 2, 3, 4, 5, 6 
A   2, 4, 6 
{The event of an even number}
The probability of A is:
n A 
P A  
n S 
3
  0.5
6
15
Example
On a particular day a statistics lecture has 260 students
attending. There are 65 mature aged students in the
lecture.
If one student is selected at random, what is the
probability that a mature age student is selected?
S ={all the students in the lecture}
M = {mature age students in the lecture}
n M  65
P M  

 0.25
n S  260
16
Complement of an event
The complement of an event are those members of the
sample space that are not contained within the event.
~
A
A
A
c
Complement rule
 
P A  1  P A 
17
Example
When rolling a die, event A is defined
as the even numbers. Find
A:
Sample Space
1
3
5
A
2
4
6
A
P ( A )  1  P ( A)
3
 1
6
 0. 5
18
Intersection
The word used to represent the intersection of two
events is:
AND
The intersection of two events are the members that
are common to both events.
19
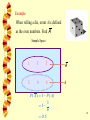
Example
When rolling a die, let A
be the event an even number
is uppermost.
A   2, 4, 6 
When rolling a die, let B be the event a
number less than three is uppermost.
B   1, 2 
20
Find the intersection of A and B.
Sample Space
It’s just me,
all alone…
1
3
5
2
4
6
21
Find the probability of
A and B.
n A and B 
P A and B  
nS 
1

6
 0.1667
22
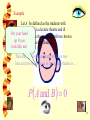
Example
Let A be defined as the students with
2 blue eyes in a lecture theatre and B
Put yourbe
hand
defined as the students with two brown
up if you
eyes in the lecture theatre.
look like me!
Then the probability students will have two
blue and two brown eyes in the lecture theatre is ...
P A and B  0
23
Mutually exclusive events
Two events are mutually exclusive when they have no
members in common.
(They don’t share any members)
Example
A is the event an even number is uppermost on a die
B is the event an odd number is uppermost on die
A
2 4 6
B
1 3 5
n( A and B)  0
P A and B   0
24
Union of events
The word used to represent the union of two events is:
OR
The union of two events are those members that are
in one event or the other event or in both.
25
Example
When rolling a die, let X be the
event an odd number is uppermost.
X   1, 3, 5 
When rolling a die, let Y be the event
a number less than five is uppermost.
Y   1, 2,3,4 
26
Find the probability of X or Y.
Sample Space
1
3
5
2
4
6
All except
for me !!
27
Therefore the probability of X or Y is
n X or Y 
P X or Y  
nS 
5

6
 0.8333
28
Addition formula
We do not always know the members of each event,
rather we only know the probabilities of these events.
In such cases, there is a formula that enables us to find
the probability of A or B:
P A or B  P A  PB  P A and B
29
Addition formula
P A or B  P A  PB  P A and B
Intersection
Sample Space
Counted once
with P(A)
A
B
Counted twice
with P(B)
30
Example
In a population the probability of being female is 0.6
and the probability of being aged 30 and over is 0.4.
The probability of being female and aged 30 and over
is 0.2. Find the probability of being either female or
aged 30 and over.
Let F represent the females in the population
Let O represent the people aged 30 and over
31
Example
In a population the probability of being female is 0.6
and the probability of being aged 30 and over is 0.4.
The probability of being female and aged 30 and over
is 0.2. Find the probability of being either female or
aged 30 and over.
PF   0.6
P O   0.4
PF and O  0.2
PF or O   PF   PO   PF and O 
 0.6  0.4  0.2
 0.8
32
Reading for next lecture
Chapter 4 sections 4.4 - 4.5
Exercise to be completed before next lecture
S&S 4.5 4.7 4.13 4.15 4.69
33