* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Relations and Functions
Functional decomposition wikipedia , lookup
Big O notation wikipedia , lookup
Structure (mathematical logic) wikipedia , lookup
Dirac delta function wikipedia , lookup
Non-standard calculus wikipedia , lookup
Continuous function wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Elementary mathematics wikipedia , lookup
Multiple integral wikipedia , lookup
History of the function concept wikipedia , lookup
Relations and Functions
Module 1 Lesson 1
What is a Relation?
A ________ is a set of ordered pairs.
When you group two or more points in a set, it is
referred to as a relation. When you want to show that a
set of points is a relation you list the points in _______.
For example, if I want to show that the points (-3,1) ;
(0, 2) ; (3, 3) ; & (6, 4) are a relation, it would be written
like this:
{(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)}
Domain and Range
Each ordered pair has two parts, an x-value
and a y-value.
The x-values of a given relation are called the
______.
The ___-values of the relation are called the
Range.
When you list the domain and range of a
relation, you place each (the domain and the
range) in a separate set of braces.
For Example,
1. List the domain and the range of the relation
{(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)}
Domain: { -3, 0, 3, 6}
Range: _______
2. List the domain and the range of the relation
{(-3,3) ; (0, 2) ; (3, 3) ; (6, 4) ; ( 7, 7)}
Domain: ________ Range: {3, 2, 4, 7}
Notice! Even though the number 3 is listed twice in the
relation, you only note the number _____ when you list the
domain or range!
Finding Domain and Range from a graph
What is the domain?
The graph to the left is of y = x2, and we can
square any number we want.
This makes the domain __________.
On a graph, the domain corresponds to the ________ axis. Since that
is the case, we need to look to the left and right to see if there are any
end points or holes in the graph to help us find our domain.
If the graph infinite to left and to the right, then the domain is
represented by all real numbers.
What's the range?
If I plug any number into this
function, am I ever going to be
able to get a negative number
as a result? No!
The range of this function is
all positive numbers which is represented by y ≥ 0.
On a graph, the range corresponds to the vertical axis. We need to
look up and down to see if there are any end points or holes to help
us find our range. If the graph keeps going up and down with no
endpoint then the range is all real numbers.
However, this is not the case here. The graph does not ever go
below the x-axis, never returning a negative range value.
What is a Function?
A function is a relation that assigns each
______ only one x-value.
What does that mean? It means, in order for the
relation to be considered a function, there cannot be
any repeated values in the domain.
There are two ways to see if a relation is a function:
1. Vertical Line Test
2. _________
Using the Vertical Line Test
Use the vertical line test to check
if the relation is a function only if
the relation is already graphed.
1.
2.
3.
4.
Hold a straightedge (pen, ruler,
etc) vertical to your graph.
Drag the straightedge from left
to right on the graph.
If the straightedge intersects
the graph once in each spot ,
then it is a function.
If the straightedge intersects the
graph more than once in any
spot, it is not a function.
A _______!
Examples of the Vertical Line Test
Mappings
If the relation is not graphed, it is easier to use what
is called a ________.
When you are creating a mapping of a relation, you
draw two ______.
In one oval, list all the _______ values.
In the other oval, list all the range values.
Draw a line connecting the pairs of domain and range
values.
If any domain value ‘maps’ to two different range
values, the relation is not a function.
It’s easier than it sounds
Example of a Mapping
Create a mapping of the following relation and
state whether or not it is a function.
{(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)}
Steps
-3
0
3
6
1
2
3
4
1.
Draw ovals
2.
List domain
3.
List range
4.
Draw lines to
connect
This relation is a _______ because each x-value maps to only one y-value.
Another Mapping
Create a mapping of the following relation and
state whether or not it is a function.
{(-1,2) ; (1, 2) ; (5, 3) ; (6, 8)}
-1
1
5
6
2
3
8
Notice that even
though there are
two 2’s in the
range, you only
list the 2 once.
This relation is a function because each x-value maps to only one y-value.
It is _____________ if two x-values go to the same y-value.
Last Mapping
Create a mapping of the following relation and
state whether or not it is a function.
{(-4,-1) ; (-4, 0) ; (5, 1) ; (3, 9)}
-4
5
3
-1
0
1
9
Make sure to list
the (-4) only once!
This relation is NOT a function because the (-4) maps to the (-1) & the (0).
It is ____________if one x-value goes to two different y-values.
Vocabulary Review
Relation:
Domain:.
Range:
Function:
Vertical Line Test:
Mapping:
Practice
Complete the following questions and check your answers on the next slide.
1.
Identify the domain and range of the following relations:
a. {(-4,-1) ; (-2, 2) ; (3, 1) ; (4, 2)}
b. {(0,-6) ; (1, 2) ; (7, -4) ; (1, 4)}
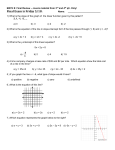
2.
Graph the following relations and use the vertical line test to see if the
relation is a function. Connect the pairs in the order given.
a. {(-3,-3) ; (0, 6) ; (3, -3)}
b. {(0,6) ; (3, 3) ; (0, 0)}
3.
Use a mapping to see if the following relations are functions:
a. {(-4,-1) ; (-2, 2) ; (3, 1) ; (4, 2)}
b. {(0,-6) ; (1, 2) ; (7, -4) ; (1, 4)}
Answers
(you will need to hit the spacebar to pull up the next slide)
1a. Domain: {-4, -2, 3, 4} Range: {-2, 2, 1}
1b. Domain: {0, 1, 7} Range: {-6, 2, -4, 4}
2a.
2b.
Function
Not a Function
3a.
3b.
-4
-2
3
4
-1
2
1
Function
0
1
7
-6
2
-4
4
Not a Function
Function Notation
The equation that represents a function is called a
_________.
A function rule is written with two variables, x
and y.
It can also be written in function notation using f(x),
where f(x) represent the y value.
F(x) is read as ‘_______________’
When you are given a function rule, you can
evaluate the function at a given domain value to find
the corresponding range value or vice versa.
……….
How to Evaluate a Function Rule
To evaluate a function rule, substitute the
value in for x and solve for y.
Examples
Evaluate the given function rules for f(2)
which is a read as let x = 2.
f(x)= x + 5
f(x)= 2x -1
f(x)= -x + 2
y=-(2)+2
y=2(2)-1
y=(2)+ 5
y= -2 + 2
y= 4 – 1
y= 7
y= 0
y= 3
……….
When f(x) equals a number
You can also be asked to let y equal a
number and then solve for x.
Examples
Evaluate the given function rules for f(x) =2
which is a read as let y = 2.
f(x)= x + 5
2= x + 5
x = ___
f(x)= 2x -1
2 =2x -1
3 = 2x
x= ____
f(x)= -x + 7
2= -x+7
-5= -x
x= ___
Evaluating for multiple values
You can also be asked to find the range
values for a given ______or vice versa.
This is the same as before, but now
you’re evaluating the same function rule for
more than one number.
The values that you are substituting in are x
values, so they are apart of the domain.
The values you are generating are y-values,
so they are apart of the ______.
Example
Steps
Find the range values of the function
for the given domain.
f(x) = -3x + 2 ; {-1, 0, 1, 2}
1.
Sub in each
domain value in
one @ a time.
2.
Solve for y in
each
3.
List y values in
braces.
y = -3x + 2
y = -3(-1) + 2
y=3+2
y = __
y = -3x + 2
y = -3(0) + 2
y=0+2
y = ___
y = -3x + 2
y = -3(1) + 2
y = -3 + 2
y = ___
y = -3x + 2
y = -3(2) + 2
y = -6 +2
y = __
The range values for the given domain are { _________}.
Find the domain
Find the domain values of the function
for the given the range values.
f(x) = 2x - 7 ; {-3, -2, 4}
y = 2x -7
-3 = 2x - 7
4 = 2x
x= 2
y = 2x -7
-2 = 2x -7
5 = 2x
x = 5/2
y = 2x - 7
4 = 2x - 7
11= 2x
x= 11/2
The domain values for the given range are
{ _________}.
Practice
1. Find the range values of the function
for the given domain.
f(x) = 3x + 1 ; {-4, 0, 2}
2. Find the domain values of the function
for the given range.
f(x) = -2x + 3 ; {-5, -2, 6}
Steps
1.
Sub in each value in one @ a time.
2.
Solve for the unknown in each
3.
List results in braces.
Answers
1. y = 3x + 1
y = 3(-4) + 1
y = -12 + 1
y = -11
2. y = -2x + 3
-5 = -2x + 3
-8 = -2x
x=4
y = 3x + 1
y = 3(0) + 1
y=0+1
y=1
Ans. { -11, 1, 7}
y = 3x + 1
y = 3(2) + 1
y=6+1
y=7
y = -2x + 3
-2 = -2x + 3
-5 = -2x
x = 5/2
Ans. {4, 5/2 , -3/2}
y = -2x + 3
6 = -2x + 3
3 = -2x
x = 3/-2