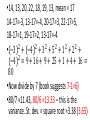* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 5 - Vanderbilt
Survey
Document related concepts
Transcript
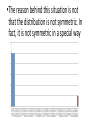
Lecture 5 The center of symmetric distributions: the mean •Besides the median, there is one more good measurement of the “center” •It works especially well if the distribution is symmetric 𝑇𝑜𝑡𝑎𝑙 𝑛 𝑛 𝑖=1 𝑦𝑖 •𝑦 = = 𝑛 collected values - the average of all Example 75.60946 47.67863 13.4834 68.27895 67.70208 27.63657 10.97026 52.80463 86.75896 35.4131 92.91208 89.27507 50.14048 13.405 49.27678 65.42801 13.67298 Median ≈50.14 The mean is 50.61 Interpretation of mean (or average) •“Center of mass”: if we have points with assigned masses, the “center of mass” is •In the same way, the mean is a point where the histogram balances Mean or median? •This is a tough question. For many “scientific” purposes, the mean is a lot better than the median. The notion of “Expectation” (which is a generalized mean) is central in Probability and Statistics Mean or median vol. 2 •However, in some situations median is more “stable”. For example, if we collect ages of students in a class, and typically it’s, say, 18, 19, 20; but then there is a 70 y.o. student. 18,18,18,18,18,19,19,19,19,19,20,20,20, 20,20, 70 With or without the 70, median is = 19. With the 70, mean is = 22.19 Without the 70, mean is = 19 So with the obvious outlier, mean does not represent an “average” student. •The reason behind this situation is not that the distribution is not symmetric. In fact, it is not symmetric in a special way Draw a picture! •It always helps to draw a good picture and look at the histogram. It often clarifies, should we trust mean or median (or both). •Sometimes people throw away top and bottom 10% of the data and average the rest. The spread: the standard deviation •This should tell us how far actual values are from the mean, in average (𝑦𝑖 −𝑦) . 𝑛 •Take This is always equal to 0 •The reason is: some of the terms are positive, and some are negative. Since the mean perfectly balances things, they add up to 0 Staying positive •To destroy all negative terms, we square them. 2 •𝑠 = 2 •𝑠 𝑦𝑖 − 𝑦 2 𝑛 2 or 𝑠 = 𝑦𝑖 −𝑦 2 𝑛−1 is called the “variance”, and 𝑠 = 𝑠 2 is called “standard deviation” •It is certainly correct to divide by n, but the book suggests to divide by n-1. Example •14, 13, 20, 22, 18, 19, 13 •First find the mean: (14+13+20+22+18+19+13)/7 = 17 •Now find (data value – mean): 14-17=-3, 13-17=-4, 20-17=3, 22-17=5, 18-17=1, 19-17=2, 13-17=-4 •14, 13, 20, 22, 18, 19, 13, mean = 17 14-17=-3, 13-17=-4, 20-17=3, 22-17=5, 18-17=1, 19-17=2, 13-17=-4 2 2 2 2 2 2 • −3 + −4 + 3 + 5 + 1 + 2 + 2 −4 = 9 + 16 + 9 + 25 + 1 + 4 + 16 = 80 •Now divide by 7 (book suggests 7-1=6) •80/7 ≈11.43, 80/6 ≈13.33 – this is the variance. St. dev. = square root ≈3.38 (3.65) Glance into future: why do we need all that? •We will rely on the following fact: if the distribution is “normal”, then most of the data should be between (mean – 3*st.dev.) and (mean+3*st.dev.) That is, if we know that our distribution is nice, then it is more or less enough to know only mean and standard deviation •On professors side, most of the scores (in a single test and total) should fall into mentioned interval •In a sense, “curve” means that professor adjusts the scores to make this happen. Why it’s good to pay attention •On the quiz tomorrow you will be allowed to use a calculator. Please bring one! Understanding and comparing distributions Magnitudes only •South America: 6.7 8.2 7.6 5.1 4.9 7.1 8.3 5.3 6.9 7.6 7.6 Median = 7.1 Mean = 6.84 •North America: 5.1 7.2 6.4 7.9 6.9 6.1 6.3 6.0 6.9 Median = 6.4 Mean = 6.53 The distribution for North America is more symmetric; also in South America a typical magnitude is higher