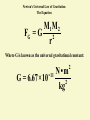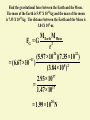Download Gravitational Forces

The Force of Gravity
We know that the Moon orbits the Earth.
Is there a force on the Moon?
Yes!!!!
How do you know?
The Moon is moving in a circular
path around the Earth - It is
changing directions
What Type of force is this and
what supplies it?
It is a centripetal force and it is
provided by the gravitational
force between the Earth & the
Moon.
What does Newton's Third Law say
about this?
Since the Earth pulls on the Moon
with its gravity, the moon pulls on the
Earth with its gravity.
What do we call these two forces?
They are an action-reaction pair.
How do these action-reaction
pairs compare?
They are the same
magnitude (size)!!!
So, the Earth pulls on the Moon with a gravitational force.
Newton’s Third Law of Motion tells us that the moon must also be
pulling on the Earth!!
We see this in the tides. The Moon’s gravitational pull on the
Earth pulls on the water, raising its level.
Newton’s Third Law also tells us that the Moon’s gravitational pull
on the Earth is the same size as the Earth’s gravitational force on
the Moon. EVEN THOUGH THE MOON IS MUCH
SMALLER!!!!!!
This would be a VERRRRRRRRRRY important thing to
remember for the test on Friday!!!!!! {HINT,HINT}
Newton's Thought Experiment
Firing cannon balls around the Earth
If you were to fire a cannonball horizontally from the top of
a large mountain, what happens?
Fire
it11.3
slowly!!
Fire
aatlittle
faster!!
faster!!
Fireit
iteven
km/s!!
It falls towards the Earth in a curved (parabolic) path. At just the
right speed (11.3 km/s) the cannonball's curved path matches the
curvature of the Earth and the cannonball falls around the Earth.
It is in orbit.
This is how we put satellites into orbit around the Earth.
We say that satellites are in Free Fall around the Earth.
This is why astronauts experience weightlessness while orbitting the
Earth, they are falling around the Earth!!!
It is NOT because there is no gravity!!!!!!
We can say the Moon is falling around the Earth.
I guess Chicken Little was right!!!!
Newton's Universal Law of Gravitation
Every object with mass attracts every other object with mass with a gravitational force.
If it has mass, it has a gravitational pull – dust, small rocks, even you!!!!!
This gravitational force is directly proportional to product of the masses of BOTH objects.
1)
The more mass an object has, the more gravitational pull it has!!
2)
The gravitational pull between two objects depends on both masses (Newton’s Third
Law)!!!
This gravitational force is inversely proportional to the square of the distance
between the centers of the two objects.
1)
If the two objects get farther apart, then the gravitational force between them
decreases very quickly.
2)
If the two objects get closer together, then the gravitational force between them
increases very quickly.
3)
The gravitational pull of an object extends forever (to infinity), although it gets real
small really fast.
Newton's Universal Law of Gravitation
The Equation
M 1M 2
FG = G
2
r
Where G is known as the universal gravitational constant:
N
•
m
-11
G = 6.67 × 10
2
kg
2
Find the gravitational force between the Earth and the Moon.
The mass of the Earth is 5.97 X 1024-kg and the mass of the moon
is 7.35 X 1022-kg. The distance between the Earth and the Moon is
3.84 X 108-m.
M Earth M Moon
FG = G
2
r
24
22
- 11 (5.97 × 10 )( 7.35 × 10 )
= (6.67 × 10 )
8 2
( 3.84 × 10 )
37
2.93 × 10
=
17
1.47 × 10
20
= 1.99 × 10 N
The gravitational force between these two objects is 100-N.
What will happen to the gravitational force if the red object’s mass doubles?
Since only the mass of only one object changes, it is all that affects the
change in the gravitational force.
FG ∝M1 → 2
So doubling the mass also doubles the gravitational force:
FG NEW = 2 × FG = 2 × 100 = 200 N
The gravitational force between these two objects is 100-N.
What will happen to the gravitational force if the
BOTH objects’ mass doubles?
Since both masses change, it is the product of the masses that affects the
change in the gravitational force.
FG ∝M1M 2 → (2)( 2)=4
So doubling both masses quadruples the gravitational force:
FG NEW = 4 × FG = 4 × 100 = 400 N
The gravitational force between these two objects is 100-N.
What will happen to the gravitational force if the
distance between the objects doubles?
Since only the distance changes, it is all that affects the change in the
gravitational force.
1
1
1
FG ∝ 2 →
2 =
r
( 2)
4
So doubling the distance gets you one fourth the gravitational force:
FG NEW
1
1
= × FG = × 100 = 25 N
4
4
The gravitational force between these two objects is 100-N.
What will happen to the gravitational force if the
distance between them is cut in half?
Since only the distance changes, it is all that affects the change in the
gravitational force.
1
1
1
FG ∝ 2 → 1 2 = 1 = 4
r
(2)
4
So halving the distance gets you four times the gravitational force:
FG NEW = 4 × FG = 4 × 100 = 400 N
The gravitational force between two objects is 75-N. If the mass of
one object doubles, the mass of the other object triples and the
distance between them is cut in half, find the new gravitational force
between these two objects.
M 1M 2
( 2)( 3) 6
FG ∝ 2 → 1 2 = 1 = 6 × 4 = 24
r
(2)
4
SO……
FG New = 24 × FG = 24 × 75 = 1800 N