Download ECE 3323 Section 2.1 Signals Power and Energy

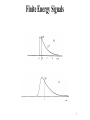
ECE 3323
Principles of Communication
Systems
Section 2.1
Signals Power and Energy
1
Definition of a Signal
A Signal, denoted x(t), is assumed to be either a
voltage or a current in an electrical system. Signals
will be assumed to be Real Functions (as opposed to
Complex, with real and imaginary parts) unless noted.
2
Signal Power
A Signal is assumed to be measured across a 1 Ω
resistance (in the case of a voltage) or measured
through a 1 Ω resistance (in the case of a current) such
that the instantaneous power of the signal is
𝑃= 𝑥 𝑡
2
Signals are assumed to be real valued, so the
instantaneous power is
𝑃 = 𝑥2 𝑡
3
Finite Energy Signals
The energy contained in a signal is the time integration
of the instantaneous power. If this quantity is bound
such that
∞
𝐸=
∞
𝑃 𝑑𝑡 =
−∞
𝑥 𝑡
2
𝑑𝑡 < ∞
−∞
the signal is known as an Energy Signal. This
requires that the signal have non-negligible magnitude
for only a finite amount of time.
4
Finite Power Signals
If a signal exists for all time, the total energy in the
signal may not be bounded. In these cases the average
power in the signal is
𝑇
𝑃𝑎𝑣𝑒
1
= lim
𝑇→∞ 𝑇
2
𝑥 𝑡
2
𝑑𝑡 < ∞
−𝑇 2
𝑃𝑎𝑣𝑒 = 𝑥 𝑡
2
<∞
The signal is said to be a Power Signal.
5
Signal Classification
Based on these two definitions, there are two classes
of signals:
1. x(t) is an Energy Signal if and only if 0 < E < ,
implying that that P = 0.
2. x(t) is a Power Signal if and only if 0 < P < ,
implying that E = .
6
Finite Energy Signals
7
Finite Power Signals
8
Periodic Signals
A signal is Periodic if and only if
𝑥 𝑡 + 𝑛𝑇0 = 𝑥 𝑡
for all t and integer n. The smallest positive number
that satisfies this condition is the period T0. All other
signals are Non – Periodic.
9
Periodic Signals
10
Deterministic Signals
Signals whose values are defined for their entire
existence are called Deterministic Signals. An
explicit mathematical expression can be written for
these signals.
11
Random Signals
Signals whose values are not defined, or not
predictable, are called Random Signals. A
mathematical expression cannot be written. Random
signals can be described by their statistical properties.
12
Continuous, Discrete, Analog or Digital?
13