Download Electric Potential - McMaster Physics and Astronomy

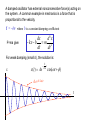
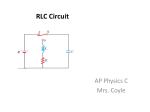
Self-Inductance and Circuits
• RLC circuits
Recall, for LC Circuits
• In actual circuits, there is always some
resistance
• Therefore, there is some energy
transformed to internal energy
• The total energy in the circuit
continuously decreases as a result of
these processes
RLC circuits
•A circuit containing a resistor,
an inductor and a capacitor is
called an RLC Circuit
•Assume the resistor represents
the total resistance of the
circuit
• The total energy is not
constant, since there is a
transformation to internal energy
in the resistor at the rate of
dU/dt = -I2R (power loss)
I
C
+
L
R
RLC circuits
The switch is closed at t =0;
Find I (t).
Looking at the energy loss in each
component of the circuit gives us:
I
C
+
L
R
EL+ER+EC=0
Which can be written as (remember, P=VI=I2R):
dI
Q
2
LI
I R  I 0
dt
C
dI
Q
L
 IR 
0
dt
C
Solution
SHM and Damping
SHM: x(t) = A cos ωt
Motion continues indefinitely.
Only conservative forces act,
so the mechanical energy is
constant.
Damped oscillator: dissipative
forces (friction, air resistance, etc.)
remove energy from the oscillator,
and the amplitude decreases with
time. In this case, the resistor
removes the energy.
x
t
x
t
A damped oscillator has external nonconservative force(s) acting on
the system. A common example in mechanics is a force that is
proportional to the velocity.
f = bv where b is a constant damping coefficient
F=ma give:
dx
d 2x
 kx  b  m 2
dt
dt
For weak damping (small b), the solution is:
x
x(t )  Ae

b
t
2m
cos(t   )
A e-(b/2m)t
t
No damping: angular frequency for spring is:
2
0 
k  b 
2
 b 

With damping:  
  0  

m  2m 
 2m 
k
m
2
The type of damping depends on the difference between
ωo and (b/2m) in this case.
b  2m 0 : “Underdamped”, oscillations with decreasing amplitude
b  2m 0 : “Critically damped”
b  2m 0 : “Overdamped”, no oscillation
x(t)
Critical damping
provides the fastest
dissipation of energy.
overdamped
critical damping
t
underdamped
RLC Circuit Compared to Damped
Oscillators
• When R is small:
– The RLC circuit is analogous to light
damping in a mechanical oscillator
– Q = Qmax e -Rt/2L cos ωdt
– ωd is the angular frequency of oscillation
for the circuit and
 1 R  
ωd  

 
 LC  2L  
2
1
2
Damped RLC Circuit, Graph
• The maximum value of
Q decreases after
each oscillation
- R<Rc (critical value)
RC  4L / C
• This is analogous to
the amplitude of a
damped spring-mass
system
Damped RLC Circuit
• When R is very large
- the oscillations damp out very rapidly
- there is a critical value of R above which
no oscillations occur:
RC  4L / C
- When R > RC, the circuit is said to be
overdamped
- If R = RC, the circuit is said to be
critically damped
Overdamped RLC Circuit, Graph
• The oscillations damp
out very rapidly
• Values of R >RC
Example: Electrical oscillations are initiated in a series circuit
containing a capacitance C, inductance L, and resistance R.
a) If R << 4 L / C (weak damping), how much time elapses
before the amplitude of the current oscillation falls off to
50.0% of its initial value?
b) How long does it take the energy to decrease to 50.0% of
its initial value?
Solution
Example: In the figure below, let R = 7.60 Ω, L = 2.20 mH, and
C = 1.80 μF.
a) Calculate the frequency of the damped oscillation of the circuit
b) What is the critical resistance?
Solution
Example: The resistance of a superconductor. In an experiment carried
out by S. C. Collins between 1955 and 1958, a current was maintained in
a superconducting lead ring for 2.50 yr with no observed loss.
If the inductance of the ring was 3.14 × 10–8 H, and the sensitivity of the
experiment was 1 part in 109, what was the maximum resistance of the
ring?
(Suggestion: Treat this as a decaying current in an RL circuit, and recall
that e– x ≈ 1 – x for small x.)
Solution