* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 1. The Baire category theorem
Surface (topology) wikipedia , lookup
Fundamental group wikipedia , lookup
Covering space wikipedia , lookup
Sheaf (mathematics) wikipedia , lookup
Michael Atiyah wikipedia , lookup
Felix Hausdorff wikipedia , lookup
General topology wikipedia , lookup
Grothendieck topology wikipedia , lookup
1. The Baire category theorem Klaus Thomsen [email protected] Institut for Matematiske Fag Det Naturvidenskabelige Fakultet Aarhus Universitet September 2005 Klaus Thomsen 1. The Baire category theorem We read in W. Rudin: Functional Analysis Klaus Thomsen 1. The Baire category theorem We read in W. Rudin: Functional Analysis Chapter 2, Starting on page 41 of my edition Klaus Thomsen 1. The Baire category theorem Definition of first and second category Klaus Thomsen 1. The Baire category theorem Definition of first and second category Let S be a topological space, i.e. Klaus Thomsen 1. The Baire category theorem Definition of first and second category Let S be a topological space, i.e. S is a set with a specified collection τ of subsets, the open sets, such that Klaus Thomsen 1. The Baire category theorem Definition of first and second category Let S be a topological space, i.e. S is a set with a specified collection τ of subsets, the open sets, such that i) S, ∅ ∈ τ , ii) when U1 , U2 , . . . , Un is a finite number of elements of τ the intersection n \ Ui i =1 is also in τ . iii) for any collection Uα , α ∈ I , of sets from τ the union [ Uα α∈I is also in τ . Klaus Thomsen 1. The Baire category theorem Definition of first and second category Example: A metric space X with metric d is a topological space: Klaus Thomsen 1. The Baire category theorem Definition of first and second category Example: A metric space X with metric d is a topological space: The open sets, τ , consists of the subsets U of X which satisfies the following condition: ∀x ∈ U ∃δ > 0 : {y ∈ X : d (y , x) < δ} ⊆ U. Klaus Thomsen 1. The Baire category theorem A subset A of S is nowhere dense when the closure A has empty interior. Klaus Thomsen 1. The Baire category theorem A subset A of S is nowhere dense when the closure A has empty interior. Reminder: The closure A of A is by definition the intersection of the closed sets containing A. The interior of any subset B ⊆ X is the union of the open sets contained in B. Klaus Thomsen 1. The Baire category theorem A subset A of S is nowhere dense when the closure A has empty interior. Reminder: The closure A of A is by definition the intersection of the closed sets containing A. The interior of any subset B ⊆ X is the union of the open sets contained in B. Thus a subset A of S is nowhere dense when the closure A does not contain any open subset. Klaus Thomsen 1. The Baire category theorem A subset A of S is nowhere dense when the closure A has empty interior. Reminder: The closure A of A is by definition the intersection of the closed sets containing A. The interior of any subset B ⊆ X is the union of the open sets contained in B. Thus a subset A of S is nowhere dense when the closure A does not contain any open subset. Examples: The integers Z is nowhere dense in R. The set { n1 : n ∈ N} is nowhere dense [0, 1]. Klaus Thomsen 1. The Baire category theorem Definition of first and second category First category A set A ⊆ S is of first category if it is the union S of a countable collection of nowhere dense sets, i.e. if A = ∞ i =1 Ai , where Ai have empty interior. Klaus Thomsen 1. The Baire category theorem Definition of first and second category First category A set A ⊆ S is of first category if it is the union S of a countable collection of nowhere dense sets, i.e. if A = ∞ i =1 Ai , where Ai have empty interior. Example: The rational numbers Q form a set of first category in the real line R. Note that Q itself is not nowhere dense; but it is the union of a countable collection of sets that are! Klaus Thomsen 1. The Baire category theorem Definition of first and second category First category A set A ⊆ S is of first category if it is the union S of a countable collection of nowhere dense sets, i.e. if A = ∞ i =1 Ai , where Ai have empty interior. Example: The rational numbers Q form a set of first category in the real line R. Note that Q itself is not nowhere dense; but it is the union of a countable collection of sets that are! A set of first category is ’small’ from the topological viewpoint. Klaus Thomsen 1. The Baire category theorem Definition of first and second category Second category A set A ⊆ S is of second category when it is not of the first category. Klaus Thomsen 1. The Baire category theorem Definition of first and second category Second category A set A ⊆ S is of second category when it is not of the first category. Via the Baire category theorem we will become able to give many examples - for example show that R is of the second category as a subset of itself. (As well as [0, 1] ⊆ R). Klaus Thomsen 1. The Baire category theorem Definition of first and second category Second category A set A ⊆ S is of second category when it is not of the first category. Via the Baire category theorem we will become able to give many examples - for example show that R is of the second category as a subset of itself. (As well as [0, 1] ⊆ R). Subsequently we shall then see why the notion is usefull ! Philosophically a set of second category is a large subset of S from the topological point of view. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (a) If A ⊆ B and B is of the first category, then so is A. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (a) If A ⊆ B and B is of the first category, then so is A. Indeed if B = S∞ i =1 Bi , then A = Klaus Thomsen S∞ i =1 Bi ∩ A and Bi ∩ A ⊆ Bi . 1. The Baire category theorem Basic properties the notions of category (a) If A ⊆ B and B is of the first category, then so is A. Indeed if B = S∞ i =1 Bi , then A = S∞ i =1 Bi ∩ A and Bi ∩ A ⊆ Bi . (b) Any countable union of sets of the first category is of the first category. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (a) If A ⊆ B and B is of the first category, then so is A. Indeed if B = S∞ i =1 Bi , then A = S∞ i =1 Bi ∩ A and Bi ∩ A ⊆ Bi . (b) Any countable union of sets of the first category is of the first category. S S∞ Indeed, if B = ∞ i =1 Bi and Bi = j=1 B(i, j ), for all i, then B(i, j ), i, j ∈ N is a countable collection of sets whose union is B. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (a) If A ⊆ B and B is of the first category, then so is A. Indeed if B = S∞ i =1 Bi , then A = S∞ i =1 Bi ∩ A and Bi ∩ A ⊆ Bi . (b) Any countable union of sets of the first category is of the first category. S S∞ Indeed, if B = ∞ i =1 Bi and Bi = j=1 B(i, j ), for all i, then B(i, j ), i, j ∈ N is a countable collection of sets whose union is B. (c) Any closed set with empty interior is of the first category. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (a) If A ⊆ B and B is of the first category, then so is A. Indeed if B = S∞ i =1 Bi , then A = S∞ i =1 Bi ∩ A and Bi ∩ A ⊆ Bi . (b) Any countable union of sets of the first category is of the first category. S S∞ Indeed, if B = ∞ i =1 Bi and Bi = j=1 B(i, j ), for all i, then B(i, j ), i, j ∈ N is a countable collection of sets whose union is B. (c) Any closed set with empty interior is of the first category. Indeed, if E is closed, E = E ∪ ∅ ∪ ∅ ∪ ∅ ∪ . . . is a union of a countable collection of nowhere dense sets. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (d) If h : S → S is a homeomorphism, E ⊆ S and h(E ) are of the same category. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (d) If h : S → S is a homeomorphism, E ⊆ S and h(E ) are of the same category. It suffices to show that h(E ) is of the first category if and only if E . Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (d) If h : S → S is a homeomorphism, E ⊆ S and h(E ) are of the same category. It suffices to show that h(E ) is of the first category if and only if E . Furthermore, since E = h−1 (h(E )), it suffice to show that h(E ) is of the first category when E is. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (d) If h : S → S is a homeomorphism, E ⊆ S and h(E ) are of the same category. It suffices to show that h(E ) is of the first category if and only if E . Furthermore, since E = h−1 (h(E )), it suffice to show that h(E ) is of the first category when S E is. So assume that E = ∞ i =1 Ei , where each Ei has empty interior. S∞ Then h(E ) = i =1 h (Ei ) and h(Ei ) = h Ei . Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (d) If h : S → S is a homeomorphism, E ⊆ S and h(E ) are of the same category. It suffices to show that h(E ) is of the first category if and only if E . Furthermore, since E = h−1 (h(E )), it suffice to show that h(E ) is of the first category when S E is. So assume that E = ∞ i =1 Ei , where each Ei has empty interior. S∞ Then h(E ) = i =1 h (Ei ) and h(Ei ) = h Ei . If U ⊆ h Ei is open, h−1 (U) ⊆ Ei is also open. Klaus Thomsen 1. The Baire category theorem Basic properties the notions of category (d) If h : S → S is a homeomorphism, E ⊆ S and h(E ) are of the same category. It suffices to show that h(E ) is of the first category if and only if E . Furthermore, since E = h−1 (h(E )), it suffice to show that h(E ) is of the first category when S E is. So assume that E = ∞ i =1 Ei , where each Ei has empty interior. S∞ Then h(E ) = i =1 h (Ei ) and h(Ei ) = h Ei . If U ⊆ h Ei is open, h−1 (U) ⊆ Ei is also open. Since Ei has empty interior, this implies that h−1 (U) = ∅, i.e. U = h−1 (h(U)) = ∅. Klaus Thomsen 1. The Baire category theorem The Baire’s category theorem The Baire’s category theorem. If S is either (a) a complete metric space, or (b) a locally compact Hausdorff space, then the intersection of every countable collection of dense open sets in S is dense is S. Klaus Thomsen 1. The Baire category theorem The Baire’s category theorem The Baire’s category theorem. If S is either (a) a complete metric space, or (b) a locally compact Hausdorff space, then the intersection of every countable collection of dense open sets in S is dense is S. Thus if Ei , i = 1, 2, 3, . . . , are dense and open in S, then dense in S. Klaus Thomsen 1. The Baire category theorem T∞ i =1 Ei is The Baire’s category theorem The Baire’s category theorem. If S is either (a) a complete metric space, or (b) a locally compact Hausdorff space, then the intersection of every countable collection of dense open sets in S is dense is S. Thus if Ei , i = 1, 2, 3, . . . , are dense and open in S, then dense in S. T∞ i =1 Ei is Corollary. A complete metric space or a locally compact Hausdorff space is of the second category; thus they are not the union of a countable collection of nowhere dense subsets. Klaus Thomsen 1. The Baire category theorem Proof of the corollary Reminder ?: A subset E of S is dense when E ∩ U 6= ∅ for all open and non-empty subsets U. Klaus Thomsen 1. The Baire category theorem Proof of the corollary Reminder ?: A subset E of S is dense when E ∩ U 6= ∅ for all open and non-empty subsets U. Examples: 1) Q is dense in R. Klaus Thomsen 1. The Baire category theorem Proof of the corollary Reminder ?: A subset E of S is dense when E ∩ U 6= ∅ for all open and non-empty subsets U. Examples: 1) Q is dense in R. The polynomials are dense in C [0, 1]. Klaus Thomsen 1. The Baire category theorem Proof of the corollary Reminder ?: A subset E of S is dense when E ∩ U 6= ∅ for all open and non-empty subsets U. Examples: 1) Q is dense in R. The polynomials are dense in C [0, 1]. Nullermændene er tætte i min ældste søns værelse. Klaus Thomsen 1. The Baire category theorem Proof of the corollary Reminder ?: A subset E of S is dense when E ∩ U 6= ∅ for all open and non-empty subsets U. Examples: 1) Q is dense in R. The polynomials are dense in C [0, 1]. Nullermændene er tætte i min ældste søns værelse. Proof of corollary using the theorem: Klaus Thomsen 1. The Baire category theorem Proof of the corollary Reminder ?: A subset E of S is dense when E ∩ U 6= ∅ for all open and non-empty subsets U. Examples: 1) Q is dense in R. The polynomials are dense in C [0, 1]. Nullermændene er tætte i min ældste søns værelse. Proof of corollary using the theorem: S∞ If S = where each Ei is nowhere dense, observe that T i =1cEi , T c c ∞ E ⊇ ∅= ∞ i =1 Ei and each Ei is dense and open. This i =1 i contradicts the theorem. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T∞ an open non-empty subset B0 of S. We want to show that i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T∞ an open non-empty subset B0 of S. We want to show that i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 Klaus Thomsen 1. The Baire category theorem (1) Proof of Baire’s category theorem Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T∞ an open non-empty subset B0 of S. We want to show that i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 (1) When S is a complete metric space we will require that d (y , x) ≤ 1 when x, y ∈ B1 and when S is locally compact Hausdorff we require that B1 is compact. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T∞ an open non-empty subset B0 of S. We want to show that i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 (1) When S is a complete metric space we will require that d (y , x) ≤ 1 when x, y ∈ B1 and when S is locally compact Hausdorff we require that B1 is compact. The argument for this differ in the two cases. Assume first that S is a complete metric space. Take x ∈ V1 ∩ B0 . Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T∞ an open non-empty subset B0 of S. We want to show that i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 (1) When S is a complete metric space we will require that d (y , x) ≤ 1 when x, y ∈ B1 and when S is locally compact Hausdorff we require that B1 is compact. The argument for this differ in the two cases. Assume first that S is a complete metric space. Take x ∈ V1 ∩ B0 . Since V1 ∩ B0 is open there is a 1 > δ > 0 such that {y ∈ S : d (y , x) < δ} ⊆ V1∩ B0 . Then B1 = y ∈ S : d (y , x) < 2δ has the desired property. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Before we continue the proof of Baire’s category theorem we develop a little of the general theory of locally compact Hausdorff spaces. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Before we continue the proof of Baire’s category theorem we develop a little of the general theory of locally compact Hausdorff spaces. Recall that a topological space is locally compact when every point has an open neighborhood with compact closure. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Before we continue the proof of Baire’s category theorem we develop a little of the general theory of locally compact Hausdorff spaces. Recall that a topological space is locally compact when every point has an open neighborhood with compact closure. Lemma Let X be a Hausdorff space, K a compact subset of X and p a point in the complement K c = X \K of K . There are then open sets U and W such that p ∈ U, K ⊆ W and U ∩ W = ∅. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Consider an element k ∈ K . Since X is Hausdorff there are open sets, Wk ⊆ X and Uk ⊆ X , such that k ∈ Wk , p ∈ Uk and Wk ∩ Uk = ∅. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Consider an element k ∈ K . Since X is Hausdorff there are open sets, Wk ⊆ X and Uk ⊆ X , such that k ∈ Wk , p ∈ Uk and Wk ∩ Uk = ∅. Note that the collection {Wk : k ∈ K } is an open cover of K . Since K is compact there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Consider an element k ∈ K . Since X is Hausdorff there are open sets, Wk ⊆ X and Uk ⊆ X , such that k ∈ Wk , p ∈ Uk and Wk ∩ Uk = ∅. Note that the collection {Wk : k ∈ K } is an open cover of K . Since K is compact there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and U = Uk1 ∩ Uk2 ∩ · · · ∩ UkN . Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Consider an element k ∈ K . Since X is Hausdorff there are open sets, Wk ⊆ X and Uk ⊆ X , such that k ∈ Wk , p ∈ Uk and Wk ∩ Uk = ∅. Note that the collection {Wk : k ∈ K } is an open cover of K . Since K is compact there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and U = Uk1 ∩ Uk2 ∩ · · · ∩ UkN . Corollary: In a Hausdorff space, any compact subset is closed. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Consider an element k ∈ K . Since X is Hausdorff there are open sets, Wk ⊆ X and Uk ⊆ X , such that k ∈ Wk , p ∈ Uk and Wk ∩ Uk = ∅. Note that the collection {Wk : k ∈ K } is an open cover of K . Since K is compact there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and U = Uk1 ∩ Uk2 ∩ · · · ∩ UkN . Corollary: In a Hausdorff space, any compact subset is closed. Proof: By Lemma1 the complement of a compact set is open. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Lemma Let X be a Hausdorff space T and {Kα : α ∈ A} a collection of compact subsets of T X . If α∈A Kα = ∅, there is a finite subset F ⊆ A such that α∈F Kα = ∅. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Lemma Let X be a Hausdorff space T and {Kα : α ∈ A} a collection of compact subsets of T X . If α∈A Kα = ∅, there is a finite subset F ⊆ A such that α∈F Kα = ∅. Proof. T Fix one of the Kα ’s; say Kα1 . Since α∈A Kα = ∅, every element of Kα1 is in the complement Kαc of Kα , for some α. This means that {Kαc : α ∈ A} covers Kα1 . Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Lemma Let X be a Hausdorff space T and {Kα : α ∈ A} a collection of compact subsets of T X . If α∈A Kα = ∅, there is a finite subset F ⊆ A such that α∈F Kα = ∅. Proof. T Fix one of the Kα ’s; say Kα1 . Since α∈A Kα = ∅, every element of Kα1 is in the complement Kαc of Kα , for some α. This means that {Kαc : α ∈ A} covers Kα1 . By Corollary ?? each Kαc is open, so by compactness of Kα1 there is a finite subset F0 ⊆ A such that [ Kα1 ⊆ Kαc . α∈F0 Set F = {α1 } ∪ F0 . Then T α∈F Klaus Thomsen Kα = ∅. 1. The Baire category theorem On locally compact Hausdorff spaces Lemma Let X be a topological space. a) The union of a finite number of compact sets in X is itself compact. b) If K is a compact subset of X and B ⊆ K is a closed subset of K , then B is compact. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Lemma Let X be a topological space. a) The union of a finite number of compact sets in X is itself compact. b) If K is a compact subset of X and B ⊆ K is a closed subset of K , then B is compact. Proof. a) is left to the reader. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Lemma Let X be a topological space. a) The union of a finite number of compact sets in X is itself compact. b) If K is a compact subset of X and B ⊆ K is a closed subset of K , then B is compact. Proof. a) is left to the reader. To prove b), consider an open cover {Uα : α ∈ A} of B. Then {B c } ∪ {Uα : α ∈ A} is an open cover of K and hence [ K ⊆ Bc ∪ Uα α∈F for some finite collection F ⊆ A. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. S It follows that B ⊆ α∈F Uα , proving that B is compact. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. S It follows that B ⊆ α∈F Uα , proving that B is compact. Lemma Let X be a locally compact Hausdorff space, K a compact subset of X and U an open subset of X such that K ⊆ U. There is then an open set V in X with compact closure V such that K ⊆ V ⊆ V ⊆ U. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Since X is locally compact we can, for each k ∈ K , find an open set Wk such that k ∈ Wk and Wk is compact. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Since X is locally compact we can, for each k ∈ K , find an open set Wk such that k ∈ Wk and Wk is compact. Since {Wk : k ∈ K } is an open cover of K , and K is compact, there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and note that W ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Since X is locally compact we can, for each k ∈ K , find an open set Wk such that k ∈ Wk and Wk is compact. Since {Wk : k ∈ K } is an open cover of K , and K is compact, there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and note that W ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . It follows from Lemma 3 that W is compact. This completes the proof in the case where U = X , since we can then take V = W . Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Since X is locally compact we can, for each k ∈ K , find an open set Wk such that k ∈ Wk and Wk is compact. Since {Wk : k ∈ K } is an open cover of K , and K is compact, there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and note that W ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . It follows from Lemma 3 that W is compact. This completes the proof in the case where U = X , since we can then take V = W . When U 6= X , let C = U c be the complement of U in X . For each / Wp′ . p ∈ C there is an open set Wp′ such that K ⊆ Wp′ and p ∈ This follows from Lemma 1. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. Since X is locally compact we can, for each k ∈ K , find an open set Wk such that k ∈ Wk and Wk is compact. Since {Wk : k ∈ K } is an open cover of K , and K is compact, there is a finite collection k1 , k2 , . . . , kN such that K ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . Set W = Wk1 ∪ Wk2 ∪ · · · ∪ WkN and note that W ⊆ Wk1 ∪ Wk2 ∪ · · · ∪ WkN . It follows from Lemma 3 that W is compact. This completes the proof in the case where U = X , since we can then take V = W . When U 6= X , let C = U c be the complement of U in X . For each / Wp′ . p ∈ C there is an open set Wp′ such that K ⊆ Wp′ and p ∈ This follows from Lemma 1. Note that \ C ∩ W ∩ Wp′ = ∅, p∈C and that each set C ∩ W ∩ Wp′ is compact. Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. It follows from Lemma 2 that there is a finite set, p1 , p2 , . . . , pN , such that N \ (2) C ∩ W ∩ Wp′i = ∅. i =1 Klaus Thomsen 1. The Baire category theorem On locally compact Hausdorff spaces Proof. It follows from Lemma 2 that there is a finite set, p1 , p2 , . . . , pN , such that N \ (2) C ∩ W ∩ Wp′i = ∅. i =1 Set V = W ∩ Wp′1 ∩ Wp′2 ∩ · · · ∩ Wp′N . Then K ⊆ V ⊆ V ⊆ W ∩ Wp′1 ∩ Wp′2 ∩ · · · ∩ Wp′N . It follows from (2) that W ∩ Wp′1 ∩ Wp′2 ∩ · · · ∩ Wp′N ⊆ U and from Lemma 3 that V is compact. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T an open non-empty subset B0 of S. We want to show that ∞ i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 Klaus Thomsen 1. The Baire category theorem (3) Proof of Baire’s category theorem - continued Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T an open non-empty subset B0 of S. We want to show that ∞ i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 (3) When S is a complete metric space we will require that d (y , x) ≤ 1 when x, y ∈ B1 and when S is locally compact Hausdorff we require that B1 is compact. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Let VT 1 , V2 , V3 , . . . be open and dense subsets of S. We must show that ∞ i =1 Vi is dense in S when S is either a complete metric space or a locally compact Hausdorff space. Consider T an open non-empty subset B0 of S. We want to show that ∞ i =1 Vi ∩ B0 6= ∅. Since V1 is dense in S, B0 ∩ V1 6= ∅. We claim that there is an open set B1 such that B1 ⊆ V1 ∩ B0 (3) When S is a complete metric space we will require that d (y , x) ≤ 1 when x, y ∈ B1 and when S is locally compact Hausdorff we require that B1 is compact. This is now straightforward in case of a locally compact Hausdorff space; thanks to the last lemma. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Next we find an open set B2 such that B2 ⊆ V2 ∩ B1 such that d (y , x) ≤ 21 when S is complete metric space and such that B2 is compact when S is a locally compact Hausdorff space. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Next we find an open set B2 such that B2 ⊆ V2 ∩ B1 such that d (y , x) ≤ 21 when S is complete metric space and such that B2 is compact when S is a locally compact Hausdorff space. This is done as above: Since V2 is dense, V2 ∩ B1 is not empty. Repeat then the previous arguments. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Next we find an open set B2 such that B2 ⊆ V2 ∩ B1 such that d (y , x) ≤ 21 when S is complete metric space and such that B2 is compact when S is a locally compact Hausdorff space. This is done as above: Since V2 is dense, V2 ∩ B1 is not empty. Repeat then the previous arguments. Thus we construct recursively a sequence B0 , B1 , B2 , . . . of open sets such that Bn ⊆ Vn ∩ Bn−1 for all n ≥ 1, d (x, y ) ≤ n1 when x, y ∈ Bn in the case where S is a complete metric space, and such that Bn is compact in the case where S is a locally compact Hausdorff space. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued The proof is now completed as follows; first the case when S is a locally compact Hausdorff space: Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued The proof is now completed as follows; first the case when S is a locally compact Hausdorff space: B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and each Bk , k ≥ 1, is compact and non-empty. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued The proof is now completed as follows; first the case when S is a locally compact Hausdorff space: B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and each Bk , k ≥ 1, is compact and non-empty. T It follows that ∞ k=1 Bk 6= ∅. Since Bk ⊆ Vk−1 for all k, we find that ∞ ∞ \ \ Vk . Bk ⊆ k=1 Klaus Thomsen k=0 1. The Baire category theorem Proof of Baire’s category theorem - continued The proof is now completed as follows; first the case when S is a locally compact Hausdorff space: B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and each Bk , k ≥ 1, is compact and non-empty. T It follows that ∞ k=1 Bk 6= ∅. Since Bk ⊆ Vk−1 for all k, we find that ∞ ∞ \ \ Vk . Bk ⊆ k=0 k=1 But T∞ k=1 Bk ⊆ B0 , so we see that ∞ \ Bk ⊆ k=1 ∞ \ Vk ∩ B0 , k=1 which was what we wanted to prove. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and ∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. To see this, let ǫ > 0 be given. Choose N so large that N1 ≤ ǫ. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. To see this, let ǫ > 0 be given. Choose N so large that N1 ≤ ǫ. Let n, m ≥ N. Then xn , xm ∈ BN , and hence d (xn , xm ) ≤ N1 ≤ ǫ. Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. To see this, let ǫ > 0 be given. Choose N so large that N1 ≤ ǫ. Let n, m ≥ N. Then xn , xm ∈ BN , and hence d (xn , xm ) ≤ N1 ≤ ǫ. Thus {xk }∞ k=1 is a Cauchy sequence in S and we set x = limk→∞ xk . Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. To see this, let ǫ > 0 be given. Choose N so large that N1 ≤ ǫ. Let n, m ≥ N. Then xn , xm ∈ BN , and hence d (xn , xm ) ≤ N1 ≤ ǫ. Thus {xk }∞ k=1 is a Cauchy sequence in S and we set x = limk→∞ xk . Since xn ∈ Bk when n ≥ k, we conclude that x ∈ Bk . Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. To see this, let ǫ > 0 be given. Choose N so large that N1 ≤ ǫ. Let n, m ≥ N. Then xn , xm ∈ BN , and hence d (xn , xm ) ≤ N1 ≤ ǫ. Thus {xk }∞ k=1 is a Cauchy sequence in S and we set x = limk→∞ xk . Since xn ∈ Bk when n ≥ k, we conclude that x ∈ Bk . (Indeed, if x ∈ / Bk there is a δ > 0 such that c {y ∈ S : d (y , x) < δ} ⊆ Bk . Since xn ∈ {y ∈ S : d (y , x) < δ} for all large n, this is a contradiction.) Klaus Thomsen 1. The Baire category theorem Proof of Baire’s category theorem - continued Finally the completion of the proof in the case of a complete metric space: T∞ T∞ As above B0 ⊇ B1 ⊇ B2 ⊇ B3 ⊇ . . . and T∞ k=1 Bk ⊆ k=0 Vk ∩ B0 . It remains therefore only to show that k=1 Bk 6= ∅. Choose xk ∈ Bk . We claim that {xk }∞ k=1 is a Cauchy sequence in S. To see this, let ǫ > 0 be given. Choose N so large that N1 ≤ ǫ. Let n, m ≥ N. Then xn , xm ∈ BN , and hence d (xn , xm ) ≤ N1 ≤ ǫ. Thus {xk }∞ k=1 is a Cauchy sequence in S and we set x = limk→∞ xk . Since xn ∈ Bk when n ≥ k, we conclude that x ∈ Bk . (Indeed, if x ∈ / Bk there is a δ > 0 such that c {y ∈ S : d (y , x) < δ} ⊆ Bk . Since xn ∈ {y ∈ S : d (y , x) < δ} for all largeTn, this is a contradiction.) Hence x ∈ ∞ k=1 Bk and the proof is complete! Klaus Thomsen 1. The Baire category theorem




















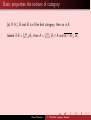




































































![Forms [14 CM] and [43 W] through [43 AC] [14 CM] Kolany`s](http://s1.studyres.com/store/data/014889156_1-4ddf6cb6c42621168d150358ab1c3978-150x150.png)










