Download Lecture containing numerical examples

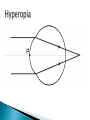
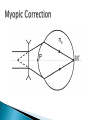
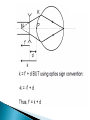
Ian Marshall




Explain emmetropia and ametropia in real eyes,
the simplified schematic eyes and the reduced
eye.
Explain spherical ametropia (myopia and
hypermetropia), axial, curvature and index
ametropia in schematic, reduced and real eyes.
The growth of the human eye in emmetropia,
spherical ametropia and progressive myopia.
Describe the correction of spherical
ametropia in the reduced eye with a thin lens.
Define ocular refraction, spectacle refraction
and vertex distance and use equations relating to
them.


Ametropia will be considered in terms of the
standard +60 D reduced eye
Draw and label a reduced eye

Since there is only a single refracting surface,
the eye is said to have an equivalent power
which is +60 D

In myopia the positive power of the eye is too
great to bring the focus onto the macula
How can we solve myopia without artificial correction?









Axial myopia: axial length > 22.22 mm
Fe = +60 D
ne = 4/3
Curvature myopia: axial length = 22.22 mm
Fe = >+60 D
ne = 4/3
Index myopia: axial length = 22.22 mm
Fe = +60 D
ne = >4/3


Axial length reaches its adult size at about 13
years of age
For babies and young people?


Myopia of more than 10D in young persons
Axial length continues to grow past 13 years
of age









Axial hyperopia: axial length <22.22 mm
Fe = +60 D
ne = 4/3
Curvature hyperopia: axial length = 22.22
mm
Fe = <+60 D
ne = 4/3
Index hyperopia: axial length = 22.22 mm
Fe = +60 D
ne = <4/3
K = Vergence incident at the reduced surface when
the rays appear to come from M
K is called the ocular refraction
K=1/k
K’ would be the vergence of light leaving the reduced surface

What is the equation for the power of the eye?
The vergence leaving the lens is equal to the
lens power

f’= k + d refers to optical distances, whereas
we are more interested in optical powers.
Rearranging the equation by taking
reciprocals of both sides gives:


This is the step back equation
Rearranging to make K the subject gives the
step along equation

To correct hyperopia, a positive spectacle
lens is placed at a point where its focus F’
coincides with M




In emmetropia K = 0
K is a constant for a particular eye, and the
power of the spectacle lens F is dependent on
the distance, d it is from the front of the eye:
For a given myopic eye, the further the
spectacle lens is placed away from the eye
the more powerful it must become
For a given hyperopic eye, the further the
spectacle lens is placed away from the eye,
the less powerful it must become