Download SRWColAlg6_06_03

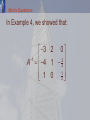
College Algebra
Sixth Edition
James Stewart  Lothar Redlin

Saleem Watson
6
Matrices
and Determinants
6.3
Inverses of Matrices
and Matrix Equations
Introduction
In the preceding section, we saw that, when
the dimensions are appropriate, matrices
can be added, subtracted, and multiplied.
Here, we investigate division of matrices.
• With this operation, we can solve equations
that involve matrices.
The Inverse of a Matrix
Identity Matrices
First, we define identity matrices.
• These play the same role for matrix
multiplication as the number 1 does for
ordinary multiplication of numbers.
• That is,
1·a=a·1=a
for all numbers a.
Identity Matrices
A square matrix is one that has the
same number of rows as columns.
The main diagonal of a square matrix
consists of the entries whose row and
column numbers are the same.
• These entries stretch diagonally down
the matrix—from top left to bottom right.
Identity Matrix—Definition
The identity matrix In is the n x n
matrix for which:
• Each main diagonal entry is a 1.
• All other entries are 0.
Identity Matrices
Thus, the
2 x 2, 3 x 3, and 4 x 4
identity matrices are:
1
1 0 0

0
1 0



I2  
I

0
1
0
I

3
4



0
0 1
0 0 1

0
0
1
0
0
0
0
1
0
0

0
0

1
Identity Matrices
Identity matrices behave like the number 1
in the sense that
A · In = A
and
In · B = B
whenever these products are defined.
E.g. 1—Identity Matrices
The following matrix products show
how:
• Multiplying a matrix by an identity matrix
of the appropriate dimension leaves
the matrix unchanged.
E.g. 1—Identity Matrices
 1 0  3 5 6  3 5 6
0 1  1 2 7    1 2 7 


 

1
1

1
7
1
0
0

1
7

 
2
2
12 1 3  0 1 0   12 1 3 



 
 2 0 7  0 0 1  2 0 7 
Inverse of a Matrix
If A and B are n x n matrices, and
if AB = BA = In, then we say that B is
the inverse of A, and we write B = A–1.
• The concept of the inverse of a matrix
is analogous to that of the reciprocal
of a real number.
Inverse of a Matrix—Definition
Let A be a square n x n matrix.
If there exists an n x n matrix A–1 with
the property that
AA–1 = A–1A = In
then we say that A–1 is the inverse of A.
E.g. 2—Verifying That a Matrix Is an Inverse
Verify that B is the inverse of A,
where:
2 1
A

5 3 
and
 3 1
B

 5 2 
• We perform the matrix multiplications
to show that AB = I and BA = I.
E.g. 2—Verifying That a Matrix Is an Inverse
2 1  3 1
AB  



5 3   5 2 
 2  3  1( 5) 2( 1)  1 2 


5  3  3( 5) 5( 1)  3  2 
1 0


 0 1
E.g. 2—Verifying That a Matrix Is an Inverse
 3 1 2
BA  


 5 2   5
 3  2  ( 1)5

( 5)2  2  5
1 0


 0 1
1

3
3  1  ( 1)3 

( 5)1  2  3 
Finding the Inverse
of a 2 x 2 Matrix
Finding the Inverse of a 2 x 2 Matrix
The following rule provides a simple way
for finding the inverse of a 2 x 2 matrix,
when it exists.
• For larger matrices, there is a more general
procedure for finding inverses—which we
consider later in this section.
Inverse of a 2 x 2 Matrix
If
a b 
A

c d 
then
 d
1
A 

ad  bc  c
1
b 

a
• If ad – bc = 0, then A has no inverse.
E.g. 3—Finding the Inverse of a 2 x 2 Matrix
Let A be the matrix
4 5
A

2 3
Find A–1 and verify that
AA–1 = A–1A = I2
E.g. 3—Finding the Inverse of a 2 x 2 Matrix
Using the rule for the inverse of a 2 x 2
matrix, we get:
 3 5 
1
1
A 


4  3  5  2  2 4 
3
5
3

5




1
2
2
 



2  2 4   1 2 
• To verify that this is indeed the inverse of A,
we calculate AA–1 and A–1A.
E.g. 3—Finding the Inverse of a 2 x 2 Matrix
3
5
4
5




1
2
2
AA  



 2 3   1 2 
 4  32  5( 1) 4(  52 )  5  2   1 0 
 3


5
 2  2  3( 1) 2(  2 )  3  2  0 1
3
5
4 5


1
2
2 
A A



 1 2   2 3 
 32  4  (  52 )2 32  5  (  52 )3   1 0 




 ( 1)4  2  2 ( 1)5  2  3  0 1
Determinant of a Matrix
The quantity ad – bc that appears in
the rule for calculating the inverse of
a 2 x 2 matrix is called the determinant
of the matrix.
• If the determinant is 0, then the matrix does not
have an inverse (since we cannot divide by 0).
Finding the Inverse
of an n x n Matrix
Finding the Inverse of an n x n Matrix
For 3 x 3 and larger square matrices,
the following technique provides
the most efficient way to calculate their
inverses.
Finding the Inverse of an n x n Matrix
If A is an n x n matrix, we first construct the
n x 2n matrix that has the entries of A on the
left and of the identity matrix In on the right:
 a11 a12
a
a
21
22



an1 an 2
a1n
a2n
1 0
0 1
ann
0 0
0

0


1
Finding the Inverse of an n x n Matrix
We then use the elementary row operations
on this new large matrix to change the left
side into the identity matrix.
• This means that we are changing the large matrix
to reduced row-echelon form.
 a11 a12
a
a
21
22



an1 an 2
a1n
a2n
1 0
0 1
ann
0 0
0

0


1
Finding the Inverse of an n x n Matrix
The right side is transformed
automatically into A–1.
• We omit the proof of this fact.
 a11 a12
a
a
21
22



an1 an 2
a1n
a2n
1 0
0 1
ann
0 0
0

0


1
E.g. 4—Finding the Inverse of a 3 x 3 Matrix
Let A be the matrix
 1 2 4 


A   2 3 6 
 3 6 15 
(a) Find A–1.
(b) Verify that AA–1 = A–1A = I3.
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
We begin with the 3 x 6 matrix whose left half
is A and whose right half is the identity matrix.
 1 2 4 1 0 0 
 2 3 6 0 1 0 


 3 6 15 0 0 1
• We then transform the left half of this new matrix
into the identity matrix—by performing the following
sequence of elementary row operations on the
entire new matrix.
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
 1 2 4 1 0 0 


R2  2R1 R2

 0 1
2 2 1 0 
R3  3R1 R3
0 0
3 3 0 1
 1 2 4 1 0 0 
1R
3 3

 0 1 2 2 1 0 


0 0 1 1 0 31 
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
 1 0 0 3 2 0 
R1  2R2 R1



 0 1 2 2 1 0


0 0 1 1 0 31 
0
 1 0 0 3 2
R2  2R3 R2
 
 0 1 0 4 1  32 


1
0 0 1 1 0

3
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
We have now transformed the left half
of this matrix into an identity matrix.
• This means we’ve put the entire matrix
in reduced row-echelon form.
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
Note that, to do this in as systematic a fashion
as possible, we first changed the elements
below the main diagonal to zeros—just as we
would if we were using Gaussian elimination.
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
Then, we changed each main diagonal
element to a 1 by multiplying by
the appropriate constant(s).
 1 2 4 1 0 0 
0 1

2 2 1 0 

0 0
3 3 0 1
 1 2 4 1 0 0 
0 1 2 2 1 0 


0 0 1 1 0 31 
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
Finally, we completed the process
by changing the remaining entries
on the left side to zeros.
 1 0 0 3 2 0 
0 1 2 2 1 0 


0 0 1 1 0 31 
 1 0 0 3 2 0 
0 1 0 4 1  2 
3


1
0 0 1 1 0

3
E.g. 4—Inverse of a 3 x 3 Matrix
Example (a)
The right half is now A–1.
 3 2 0 

1
2
A   4 1  3 
1
 1 0
3
E.g. 4—Inverse of a 3 x 3 Matrix
Example (b)
We calculate AA–1 and A–1A, and verify that
both products give the identity matrix I3.
 1 2 4  3 2 0   1 0 0 





1
2
AA   2 3 6 4 1  3   0 1 0 
1
 3 6 15   1 0
0 0 1
3
 3 2 0   1 2 4   1 0 0 
A1A   4 1  32   2 3 6   0 1 0 
1
 1 0
3 6 15  0 0 1
3
Using Graphing Calculators
Graphing calculators are also able to
calculate matrix inverses.
• On the TI-83 and TI-84 calculators, matrices
are stored in memory using names such as
[A], [B], [C], . . . .
• To find the inverse of [A], we key in:
[A] x–1 ENTER
Using Graphing Calculators
For the matrix of Example 4, this results
in the output shown.
• We have also used
the Frac command
to display the output
in fraction form rather
than in decimal form.
E.g. 5—Matrix That Does Not Have an Inverse
Find the inverse of the matrix.
2 3 7 
1 2 7 


 1 1 4 
E.g. 5—Matrix That Does Not Have an Inverse
2 3 7 1 0 0 
1 2 7 0 1 0 R


 1 1 4 0 0 1
1
 R2
1 2 7 0 1 0
2 3 7 1 0 0 


 1 1 4 0 0 1
E.g. 5—Matrix That Does Not Have an Inverse
1

R2  2R1 R2

 0
R3 R1 R3
0
 71 R2

1
0

0
2
7
1
0

21 1 2 0 
 3 0 1 1 
7 0
2
7
1
3  71
1 3
0
0
1
0

2
0
7
1 1
1
E.g. 5—Matrix That Does Not Have an Inverse
2
1
0
1

7
R3 R2 R3

1


0
1
3

7
R1  2R2 R1

1
0 0 0  7

3
7
2
7
5
7
0

0

1
• At this point, we would like to change the 0
in the (3, 3) position of this matrix to a 1,
without changing the zeros in the (3, 1) and (3, 2)
positions.
E.g. 5—Matrix That Does Not Have an Inverse
2
1
0
1

7
R3 R2 R3

1


0
1
3

7
R1  2R2 R1

1
0 0 0  7

3
7
2
7
5
7
0

0

1
• However, there is no way to accomplish this.
• No matter what multiple of rows 1 and/or 2 we add
to row 3, we can’t change the third zero in row 3
without changing the first or second zero as well.
E.g. 5—Matrix That Does Not Have an Inverse
2
1
0
1

7
R3 R2 R3

1


0
1
3

7
R1  2R2 R1

1
0 0 0  7

3
7
2
7
5
7
0

0

1
• Thus, we cannot change the left half
to the identity matrix.
• So, the original matrix doesn’t have an inverse.
Matrix that Does Not Have an Inverse
If we encounter a row of zeros on
the left when trying to find an inverse—as
in Example 5—then the original matrix
does not have an inverse.
Singular Matrix
If we try to calculate the inverse of the matrix
from Example 5 on a TI-83 calculator, we get
the error message shown here.
• A matrix that has
no inverse is called
singular.
Matrix Equations
Matrix Equations
We saw in Example 6 in Section 6.2
that a system of linear equations can be
written as a single matrix equation.
Matrix Equations
For example, the system
is equivalent to the
matrix equation
x  2y  4z  7


 2 x  3 y  6z  5
3 x  6y  15z  0

 1 2 4   x  7
 2 3 6   y   5 

   
 3 6 15   z  0 
Coefficient Matrix
If we let
 1 2 4 


A   2 3 6 
 3 6 15 
x


X  y 
 z 
7 


B  5 
0 
this matrix equation can be written as:
AX = B
• The matrix A is called the coefficient matrix.
Matrix Equations
We solve this matrix equation by multiplying
each side by the inverse of A—provided
the inverse exists.
AX = B
A–1(AX) = A–1B
(A–1A)X = A–1B
I3X = A–1B
X = A–1B
Associative Property
Property of Inverses
Matrix Equations
In Example 4, we showed that:
 3 2 0 

1
2
A   4 1  3 
1
 1 0
3
Matrix Equations
So, from X = A–1B, we have:
 x   3 2 0  7   11
 y    4 1  2  5  23
3 
  


1 
 z   1 0


0
7




3
• Thus, x = –11, y = –23, z = 7
is the solution of the original system.
Matrix Equations
We have proved that the matrix
equation
AX = B
can be solved by the following method.
Solving a Matrix Equation
Let:
• A be a square n x n matrix that has an inverse A–1.
• X be a variable matrix, with n rows.
• B be a known matrix, with n rows.
Then, the solution of the matrix equation
AX = B
is given by:
X = A–1B
E.g. 6—Solving a System Using a Matrix Inverse
2 x  5 y  15

3 x  6 y  36
(a) Write the system of equations as a matrix
equation.
(b) Solve the system by solving the matrix
equation.
E.g. 6—Using a Matrix Inverse
Example (a)
We write the system as a matrix
equation of the form AX = B:
2 5   x  15 
3 6   y   36

   
E.g. 6—Using a Matrix Inverse
Example (b)
Using the rule for finding the inverse of
a 2 x 2 matrix, we get:
1
2 5 
 6 ( 5)
1
A 




2( 6)  ( 5)3  3
2 
3 6 
1  6 5 
 

3  3 2
1
E.g. 6—Using a Matrix Inverse
Example (b)
Multiplying each side of the matrix
equation by the inverse matrix, we get:
 x  1  6 5 15  30
 y   3  3 2 36   9 
 

   
• Thus, x = 30 and y = 9.
Modeling with Matrix Equations
Applications
Suppose we need to solve several
systems of equations with the same
coefficient matrix.
• Then, converting the systems to matrix equations
provides an efficient way to obtain the solutions.
• We only need to find the inverse of the coefficient
matrix once.
Applications
This procedure is particularly convenient
if we use a graphing calculator to
perform the matrix operations—as in
the next example.
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
A pet-store owner feeds his hamsters
and gerbils different mixtures of three types
of rodent food:
KayDee Food, Pet Pellets, Rodent Chow
• He wishes to feed his animals the correct amount
of each brand to satisfy their daily requirements
for protein, fat, and carbohydrates exactly.
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
Suppose that each day:
• Hamsters require
340 mg of protein
280 mg of fat
440 mg of carbohydrates
• Gerbils need
480 mg of protein
360 mg of fat
680 mg of carbohydrates
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
The amount of each nutrient (in mg)
in one gram of each brand is given here.
• How many grams of each food should the
storekeeper feed his hamsters and gerbils daily to
satisfy their nutrient requirements?
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
We let x1, x2, and x3 be the respective
amounts (in grams) of KayDee Food, Pet
Pellets, and Rodent Chow that the hamsters
should eat.
We let y1, y2, and y3 be the corresponding
amounts for the gerbils.
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
Then, we want to solve the matrix equations
10 0 20   x1  340 
10 20 10   x    280 

 2 

 5 10 30   x3   440 
10 0 20   y1   480 
10 20 10   y   360 

 2 

 5 10 30   y 3   680 
Hamster eqn.
Gerbil eqn.
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
Let:
10 0 20 
340 
 480 






A  10 20 10  B  280  C  360 
 5 10 30 
 440 
680 
 x1 


X   x2 
 x3 
 y1 


Y  y2 
 y 3 
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
Then, we can write these matrix equations
as:
AX = B Hamster eqn.
AY = C Gerbil eqn.
• We want to solve for X and Y.
• So, we multiply both sides of each equation
by A–1, the inverse of the coefficient matrix.
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
We could find A–1 by hand.
However, it is more convenient to use
a graphing calculator.
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
From the calculator displays,
we see:
10
8




1
1
X A B3
Y A C4
12
20
E.g. 7—Modeling Nutritional Requirements Using Matrix equations
Daily, each hamster should be fed:
• 10 g of KayDee Food.
• 3 g of Pet Pellets.
• 12 g of Rodent Chow.
Daily, each gerbil should be fed:
• 8 g of KayDee Food.
• 4 g of Pet Pellets.
• 20 g of Rodent Chow.