Download Similarity Proofs

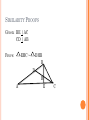
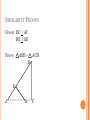
SIMILARITY PROOFS
Geometry
SIMILAR TRIANGLES

Two triangles that are the same shape but
different sizes.
E
B
A
C
D
F
Triangle ABC ~ Triangle DEF
Triangle ABC is similar to Triangle DEF
DEFINITION


In mathematics, polygons are similar if their
corresponding (matching) angles are congruent
(equal in measure) and the ratio of their
corresponding sides are in proportion.
Symbol: ~
SIMILAR TRIANGLES
SIMILAR TRIANLGES

If triangles are similar, then:
Corresponding angles are congruent:
<A is congruent to <D
<B is congruent to <E
<C is congruent to <F
Corresponding sides are in proportion.
Proportion = when 2 ratios are set equal to
each other.
CORRESPONDING SIDES

Corresponding sides are in proportion.
B
E
5 6
10
12
A 7
C
D
F
14
ANGLE-ANGLE (AA) POSTULATE OF
SIMILARITY

Two triangles are similar if two pairs of
corresponding angles are congruent.
B
E
A
C
D
If: <A = <D
<B = <E
Then: ABC ~
DEF
F
SIMILARITY PROOFS
Given:
CD is perpendicular to AB
<CAD = <BCD
Prove:
CDA ~
BDC
B
D
A
C
SIMILARITY PROOFS
Given: AB || DE
BC || EF
Prove:
ABC ~
DEF
B
E
A
C
D
F
SIMILARITY PROOFS
Given: BE | AC
CD | AB
Prove:
EHC ~
DHB
B
D
A
H
E
C
SIMILARITY PROOFS
Given: DC | AC
BE | AD
Prove:
AEB ~ ACD
D
E
A
B
C