* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download talk - Electrical and Computer Engineering
Resistive opto-isolator wikipedia , lookup
Wireless power transfer wikipedia , lookup
Power over Ethernet wikipedia , lookup
Audio power wikipedia , lookup
Opto-isolator wikipedia , lookup
Power factor wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Power inverter wikipedia , lookup
Current source wikipedia , lookup
Three-phase electric power wikipedia , lookup
Mercury-arc valve wikipedia , lookup
Electrical substation wikipedia , lookup
Stray voltage wikipedia , lookup
Electric power system wikipedia , lookup
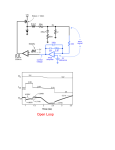
Electrification wikipedia , lookup
Distributed generation wikipedia , lookup
Surge protector wikipedia , lookup
History of electric power transmission wikipedia , lookup
Voltage optimisation wikipedia , lookup
Distribution management system wikipedia , lookup
Power electronics wikipedia , lookup
Buck converter wikipedia , lookup
Power engineering wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Mains electricity wikipedia , lookup
Vectorless Verification of RLC Power Grids with Transient Current Constraints Xuanxing Xiong and Jia Wang Electrical and Computer Engineering Illinois Institute of Technology Chicago, Illinois, United States November, 2011 Agenda Power Grid Verification Proposed Approach Experimental Results 2 Power Grid Verification Verify that the power supply noises are within certain acceptable range Noises depend on the patterns of currents drawn General idea for power grid verification First, specify currents Second, compute noises Simulation-based verification DC & Transient analysis Need to simulate a large number of current vectors to cover usual use scenarios No guarantee the worst noise (but not overpessimistic) can be found. 3 Vectorless Power Grid Verification Apply optimization to find a current vector that leads to the worst power supply noise [Kouroussis et al DAC’03] [Qian et al ISPD’04] Objective: maximizing power supply noise Constraints: feasible current set all possible current vectors No need to explicitly enumerate all possible current vectors Trade-off: accuracy of feasible current set and solution efficiency Linear current constraints: linear programming Steady-state vectorless verification For worst-case DC scenarios and provide bounds for RC powergrid. Early works are limited to small problem sizes. But recent advances [Abdul Ghani et al DAC’09] [Xiong et al DAC’10, ICCAD’10] have improved solution efficiency drastically. 4 Transient Vectorless Verification Transient behaviors are more realistic Steady-state verification could be overpessimistic. Power grid modeling Inductances [Abdul Ghani et al ICCAD’06] Capacitive couplings between VDD and GND networks [Avci et al ICCAD’10] Current modeling Max delta constraints [Ferzli et al TCAD’10] Current slope constraints [Du et al ISQED’10] Current conservation constraints [Avci et al ICCAD’10] Power constraints [Cheng et al ISPD’11] However, there is no constraint to restrict the transient behavior of individual current sources. 5 Our Contribution A framework for transient vectorless verification of RLC power grids With both VDD & GND networks Propose transient constraints for current sources To capture the fact that a gate/block will only draw current when it is switching Prove the transient vectorless verification problem can be decomposed into a transient power grid anlysis problem and an optimization problem Be able to leverage research works on fast power grid simulation 6 Agenda Power Grid Verification Proposed Approach Experimental Results 7 Integrated RLC Power Grid 8 The System Equation Time domain G: conductance M/C: represent self-inductance/capactiance links v(t): nodal voltage noises ^ I(t): current excitations Discretization with time step t where 9 Current Constraints [Kouroussis et al DAC’03] and [Avci et al ICCAD’10] Local Constraints Global Constraints Current Conservation Constraints 10 Our Transient Current Constraints Nts: number of time steps IT: nx1 upper bound vector Transient constraints may be extracted from the circuit by switching activity analysis, e.g. [Morgado et al ICSD’09] and [Morgado et al TODAES’09] 11 Our Problem Formulation For each node j The formulation actually computes the worst noise at node j for all time slots kt If the cumulative effects of voltage noises are of interests, e.g. similar to [Evmorfopoulos et al ICCAD’10], the objective function can be 12 Property of System Equation There exists a unique series of nxn matrices S1, S2, ... Sk, Sk+1, ..., such that jth column of Sk can be computed as Sk is symmetric. So 13 Our Problem Decompostion For each node j: Sub-problem I: transient analysis with current excitation ej to compute cj,k Sub-problem II: linear programming (LP) to compute worst-case voltage noises 14 Agenda Power Grid Verification Proposed Approach Experimental Results 15 Experimental Setup Implement the RLCVN in C++ Use PCG with a random-walk based preconditioner for transient analysis Adopt MOSEK to solve the LP problems Randomly generate 6 RLC power grids with 4 metal layers, 1.2V VDD, and various constraints Time step = 10ps, number of time steps Nts = 100 16 A Simple Case Study Left: no transient constraint, max voltage drop is 118.4mV. Right: IT = 200mA, max voltage drop at node j is 86.5mV. 17 Overestimation without Transient Constraints for a Random Node 18 Average Runtime per Node 19 Conclusion & Future Work The proposed transient constraints make the voltage noise predicitons more realistic. The proposed decomposition results in an effective method for transient vectorless verification. To handle even larger power grid verification problems, it is necessary to research more efficient algorithms to solve the LP problems for worst-case voltage noises. 20 Thanks! 21 Our RLCVN Algorithm Can be extended to verify the integral of voltage noise without any computational overhead 22