Download A.P. STATISTICS LESSON 6.3 (DAY 1)

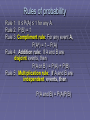
AP STATISTICS
LESSON 6.3
(DAY 1)
GENERAL PROBABILITY RULES
Warm – up # 1
Page 323 # 5.87
ESSENTIAL QUESTION:
What are general probability rules
and how are they used to solve
probability problems?
Objectives:
 To become familiar with general probability
rules.
 To use the general probability rules to solve
problems.
 To use Venn diagrams, Tree diagrams and
tables to solve probability problems.
Rules of probability
Rule 1: 0 ≤ P(A) ≤ 1 for any A.
Rule 2: P(S) = 1
Rule 3: Compliment rule: For any event A,
P(Ac) = 1 – P(A)
Rule 4: Addition rule: If A and B are
disjoint events, then
P(A or B ) = P(A) + P(B)
Rule 5: Multiplication rule: If A and B are
independent events, then
P(A and B) = P(A)P(B)
Union
The union of any collection of events is the
event that at least one of the collection
occurs.
S
B
A
C
The addition rule for disjoint events: P(A or B or
C ) = P(A) + P( B) + P(C) when events A, B,
and C are disjoint.
Addition rule for disjoint events
If events A, B, and C are disjoint in the sense
that no two have any outcomes in common,
then
P( one or more of A, B, C ) = P(A) + P(B) + P(C)
This rule extends to any number of disjoint
events.
Example 6.16
Page 361
The general addition rule for the union
of two events:
P(A or B) = P(A) + P(B) – P(A and B)
A and B
B
A
P ( A and B ) is called joint probability.
General addition rule for unions of
two events.
For any two events A and B’
P(A or B) = P(A) + P(B) – P( A and B )
Equivalently,
P(A U B ) = P(A) + P(B) – P( A ∩ B )
Example 6.17
Page 362
Conditional Probability
P(A/B) – Conditional probability – gives the
probability of one event under the
condition that we know another event.
Example 6.19
 Page 366
General Multiplication Rule for any
Two Events
The probability that both of two events A and B
happen together can be found by
P(A and B ) = P(A)P(B/A)
Here P(B/A) is the conditional probability that B
occurs given the information that A occurs.
In words, this rule says that for both of two events
to occur, first one must occur and then, given
that the first event has occurred, the second
must occur.
Example 6.20
Page 368
Definition of conditional probability
When P(A) > 0, the conditional probability of
B given A is
P(A/B) = P( A and B)
P (A)
Be sure to keep in mind the distinct roles in
P(B/A) of the event B whose probability we
are computing and the event A that
represents the information we are given.
Example 6.21
 Page 369