* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Fourier Transforms and Images
Harold Hopkins (physicist) wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Fourier optics wikipedia , lookup
Phase-contrast X-ray imaging wikipedia , lookup
Hyperspectral imaging wikipedia , lookup
Imagery analysis wikipedia , lookup
Optical coherence tomography wikipedia , lookup
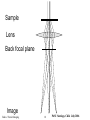
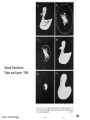
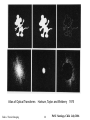
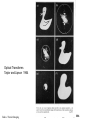
Fourier Transforms and Images Eades / Fourier Imaging 1 PASI Santiago, Chile July 2006 Our aim is to make a connection between diffraction and imaging - and hence to gain important insights into the process Eades / Fourier Imaging 2 PASI Santiago, Chile July 2006 What happens to the electrons as they go through the sample? Eades / Fourier Imaging 3 PASI Santiago, Chile July 2006 Eades / Fourier Imaging 4 PASI Santiago, Chile July 2006 What happens to the electrons a) The electrons in the incident beam are scattered into diffracted beams. b) The phase of the electrons is changed as they go through the sample. They have a different kinetic energy in the sample, this changes the wavelength, which in turn changes the phase. Eades / Fourier Imaging 5 PASI Santiago, Chile July 2006 The two descriptions are alternative descriptions of the same thing. Therefore, we must be able to find a way of linking the descriptions. The link is the Fourier Transform. Eades / Fourier Imaging 6 PASI Santiago, Chile July 2006 A function can be thought of as made up by adding sine waves. A well-known example is the Fourier series. To make a periodic function add up sine waves with wavelengths equal to the period divided by an integer. Eades / Fourier Imaging 7 PASI Santiago, Chile July 2006 Reimer: Transmission Electron Microscopy Eades / Fourier Imaging 8 PASI Santiago, Chile July 2006 The Fourier Transform The same idea as the Fourier series but the function is not periodic, so all wavelengths of sine waves are needed to make the function Eades / Fourier Imaging 9 PASI Santiago, Chile July 2006 The Fourier Transform Fourier series F (t ) Fn cos(2nt ) n0 Fourier transform f (t ) F ( ) exp 2it. d f ( x ) F(u ) exp 2iux .dx Eades / Fourier Imaging 10 PASI Santiago, Chile July 2006 So think of the change made to the electron wave by the sample as a sum of sine waves. But each sine wave term in the sum of waves is equivalent to two plane waves at different angles This can be seen from considering the Young's slits experiment - two waves in different directions make a wave with a sine modulation Eades / Fourier Imaging 11 PASI Santiago, Chile July 2006 Original figure by Thomas Young, courtesy Bradley Carroll Eades / Fourier Imaging 12 PASI Santiago, Chile July 2006 Bradley Carroll Eades / Fourier Imaging 13 PASI Santiago, Chile July 2006 Eades / Fourier Imaging 14 PASI Santiago, Chile July 2006 This analysis tells us that a sine modulation - produced by the sample with a period d, will produce scattered beams at angles q, where d and q are related by 2d sin q l we have seen this before Eades / Fourier Imaging 15 PASI Santiago, Chile July 2006 Bragg’s Law Bragg’s Law 2d sin θ = λ tells us where there are diffracted beams. Eades / Fourier Imaging 16 PASI Santiago, Chile July 2006 What does a lens do? A lens brings electrons in the same direction at the sample to the same point in the focal plane Direction at the sample corresponds to position in the diffraction pattern and vice versa Eades / Fourier Imaging 17 PASI Santiago, Chile July 2006 Sample Lens Back focal plane Image Eades / Fourier Imaging 18 PASI Santiago, Chile July 2006 Eades / Fourier Imaging 19 PASI Santiago, Chile July 2006 Eades / Fourier Imaging 20 PASI Santiago, Chile July 2006 The Fourier Transform Fourier series F (t ) Fn cos(2nt ) n0 Fourier transform f (t ) F ( ) exp 2it. d f ( x ) F(u ) exp 2iux .dx Eades / Fourier Imaging 21 PASI Santiago, Chile July 2006 Eades / Fourier Imaging 22 PASI Santiago, Chile July 2006 Eades / Fourier Imaging 23 PASI Santiago, Chile July 2006 Optical Transforms Taylor and Lipson 1964 Eades / Fourier Imaging 24 PASI Santiago, Chile July 2006 Convolution theorem F . T . f ( x ) g ( x ) F . T . f ( x ) F . T . g ( x) F ( u) G ( u ) F. T. f ( x) g( x) F (u) G(u) Eades / Fourier Imaging 25 PASI Santiago, Chile July 2006 Atlas of Optical Transforms Eades / Fourier Imaging Harburn, Taylor and Welberry 1975 26 PASI Santiago, Chile July 2006 Atlas of Optical Transforms Eades / Fourier Imaging Harburn, Taylor and Welberry 1975 27 PASI Santiago, Chile July 2006 Atlas of Optical Transforms Eades / Fourier Imaging Harburn, Taylor and Welberry 1975 28 PASI Santiago, Chile July 2006 Atlas of Optical Transforms Eades / Fourier Imaging Harburn, Taylor and Welberry 1975 29 PASI Santiago, Chile July 2006 Optical Transforms Taylor and Lipson 1964 Eades / Fourier Imaging 30 PASI Santiago, Chile July 2006 Optical Transforms Taylor and Lipson 1964 Eades / Fourier Imaging 31 PASI Santiago, Chile July 2006 Optical Transforms Taylor and Lipson 1964 Eades / Fourier Imaging 32 PASI Santiago, Chile July 2006 Atlas of Optical Transforms Eades / Fourier Imaging Harburn, Taylor and Welberry 1975 33 PASI Santiago, Chile July 2006 Atlas of Optical Transforms Eades / Fourier Imaging Harburn, Taylor and Welberry 1975 34 PASI Santiago, Chile July 2006