Download File

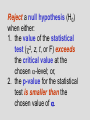
Other Types of t-tests
Recapitulation
1. Still dealing with random samples.
2. However, they are partitioned into two subsamples.
3. Interest is in whether the means of some variable
differ significantly between the two subsamples.
4. For large samples, the sampling distribution of
mean differences is normally shaped.
5. For smaller samples, the sampling distribution takes
the shape of one of the Student’s t distributions.
6. In either case, the significance tests involve a test of
the null hypothesis (H0) that in general (i.e., in the
universe) the means do NOT differ. Symbolically,
H0: 2 - 1 = 0.00
7. The alternate hypothesis (H1) can either be
nondirectional
H1: 2 - 1  0.0
or directional, either
H1: 2 - 1 > 0.0
or
H1: 2 - 1  0.0
Reject a null hypothesis (H0)
when either:
1. the value of the statistical
test (2, z, t, or F) exceeds
the critical value at the
chosen -level; or,
2. the p-value for the statistical
test is smaller than the
chosen value of .
An Example of a T-Test
PPD 404
TTEST PROCEDURE
Variable: MANUFPCT
PERCENT OF LABOR FORCE IN MANUFAC
AGECITY2
N
Mean
Std Dev
Std Error
-----------------------------------------------------------------------------Newer
38
26.52631579
10.94886602
1.77614061
Older
25
23.92000000
9.25526877
1.85105375
Variances
T
DF
Prob>|T|
--------------------------------------Unequal
1.0160
57.1
0.3139
Equal
0.9811
61.0
0.3304
For H0: Variances are equal, F' = 1.40
DF = (37,24)
Prob>F' = 0.3897
An Example of a T-Test
PPD 404
TTEST PROCEDURE
Variable: MANUFPCT
PERCENT OF LABOR FORCE IN MANUFAC
AGECITY2
N
Mean
Std Dev
Std Error
-----------------------------------------------------------------------------Newer
38
26.52631579
10.94886602
1.77614061
Older
25
23.92000000
9.25526877
1.85105375
Variances
T
DF
Prob>|T|
--------------------------------------Unequal
11.0160
57.1
0.0313
Equal
10.9811
61.0
0.0330
For H0: Variances are equal, F' = 11.40
DF = (37,24)
Prob>F' = 0.0389
The tests that we have performed thus all assumed that
the “subuniverse” variances were equal.
Remember, parameters (e.g., universe variances) are
almost always unknown. Therefore, we let subsample
variances be proxies for the unknown universe
variances.
If the two variances in the universe are greatly
different—as indicated by statistically significant
differences between the subsample variances—, then
a different method must be used to estimate the
standard error of the difference.
A hypothesis test exists to decide whether the two
variances are significantly different. In this F' test, a
ratio is computed for the larger to the smaller
subsample variance. If the variances are roughly
equal, then the value of F' should be roughly equal to
1.00 (i.e., a / a = 1). If the subsample variances are not
equal, then the F' ratio will become greater than 1.0. At
some point (i.e., beyond the critical value), the value of
the F' statistic becomes so much greater than 1.0 that it
is unlikely that the variances are equal. The test is:
l arg er s 2
F' 
smaller s 2
The null hypothesis is that the two variances are
equal (i.e., there is no difference between them):
H0: 2 - 1 = 0.0
If this hypothesis must be rejected, this means that the
variances are treated as UNEQUAL, and an adjustment
must be made in estimating the standard error of the
difference. Let's test the variances from the frostbelt and
sunbelt cities to see if they may safely be presumed to
be equal:
57.61
F' 
9.98
F '  5.773
The sample statistics were:
Frostbelt Cities
_
Y2 = - 4.14
s22 = 9.98
N2 = 37
Sunbelt Cities
_
Y1 = 2.84
s12 = 57.61
N1 =
26
This is clearly greater than 1.0, but is it sufficiently
greater to infer that the null hypothesis of equal
variances must be rejected? We need a sampling
distribution for F'. This is found in Appendix 3 (pp. 544546). Notice that the tables in this appendix are threedimensional tables, i.e., their dimensions are -levels
(pages), n1 (columns), and n2 (rows). How can we use
these tables? First, decide on the chance of being
wrong in rejecting the equal-variance null hypothesis.
Let's stick with  = 0.05. This means we are dealing
with the sampling distributions for F' on p. 544. The
columns identify critical values for the numerator
degrees of freedom (the larger variance), the rows the
denominator degrees of freedom. In this case, the
larger variance is for frostbelt cities, and df = 25 (26 - 1)
while the smaller is for sunbelt cities, df = 36 (37 - 1).
Thus we look for Column 25 (n1) and Row 36 (n2).
There is no Column 25, but df = 24 (Column 24). There
also is no Row 36, but we can interpolate. Our critical
value is 60 percent of the way between 1.89 and 1.79,
1.83 (by interpolation).
Since an F' of 5.77 is GREATER than the F' critical
value (1.83), we reject the null hypothesis and conclude
that the universe variances are probably UNEQUAL.
This means that instead of pooling to estimate the
standard error of the difference (as above), we should
calculate the t-value as follows:
Thus we look for Column 25 (n1) and Row 36 (n2).
There is no Column 25, but df = 24 (Column 24). There
also is no Row 36, but we can interpolate. Our critical
value is 60 percent of the way between 1.89 and 1.79,
1.83 (by interpolation).
Since an F' of 5.77 is GREATER than the F' critical
value (1.83), we reject the null hypothesis and conclude
that the universe variances are probably UNEQUAL.
This means that instead of pooling to estimate the
standard error of the difference (as above), we should
calculate the t-value as follows:

Y
t 
2
 Y1    2  1 
s22
s12

N2
N1
where s22 and s12 are the variances (standard deviations
squared) for the two subsamples, and N2 and N1 are the
respective subsample sizes. Our t-statistic is calculated as
t 
 6.98
9.98
57.61

37
26
 6.98
t
0.270  2.216
 6.98
t 
2.486
t 
 6.98
1.577
t  4.426
This is slightly less then t = - 5.00 calculated without
adjusting for unequal variances. Is it statistically significant?
To decide, we first must also make an adjustment in the
value of the number of degrees of freedom in order to be
sure that we are using the correct sampling distribution for
this application:
 s22

N 
 2
df 
2
2
 s2 

N 

 2

 N 2  1
2
 9.98 57.61 



37
26

df  
2
2
 9.98 
 57.61 




 37    26 
37  1 26  1
df  31.2
2
s 

N1 

2
2
 s1 

N 

 1
 N1  1
2
1
With unequal population variances, both the calculation
of t and the determination of degrees of freedom (i.e.,
the appropriate sampling distribution) must be adjusted.
This time, the critical value (in Appendix 2, p. 543) at
alpha = 0.05 (one-tailed test) is 12 percent of the way
from 1.697 to 1.684. Interpolating gives
1.697 - [0.12(1.697 – 1.684)], or 1.695
Supplying the negative sign gives us the critical value
for the left-hand tail, - 1.695. Since - 4.426 lies beyond
– 1.695 in the region of rejection, we REJECT the null
hypothesis that frostbelt and sunbelt cities lost
population at the same rate.
The SAS Procedure for t-tests
libname old 'a:\';
libname library 'a:\';
options nonumber nodate ps=66;
proc ttest data=old.cities;
class agecity2;
var manufpct;
title1 'An Example of a T-Test';
title2;
title3 'PPD 404';
run;
An Example of a T-Test
PPD 404
TTEST PROCEDURE
Variable: MANUFPCT
PERCENT OF LABOR FORCE IN MANUFAC
AGECITY2
N
Mean
Std Dev
Std Error
-----------------------------------------------------------------------------Newer
38
26.52631579
10.94886602
1.77614061
Older
25
23.92000000
9.25526877
1.85105375
Variances
T
DF
Prob>|T|
--------------------------------------Unequal
1.0160
57.1
0.3139
Equal
0.9811
61.0
0.3304
For H0: Variances are equal, F' = 1.40
DF = (37,24)
Prob>F' = 0.3897
Evaluating these t-test results is done in
two steps:
First, decide whether the (population)
variances are probably equal or unequal
(i.e., is the F' test statistically significant?).
Then, decide whether the appropriate
t-test (for unequal or equal variances)
calls for rejection of the null hypothesis of
no difference between means.
Reject the null hypothesis (H0)
when either:
1. the value of the statistical
test (2, z, t, F', or F) exceeds
the critical value at the
chosen -level; or,
2. the p-value for the statistical
test is smaller than the chosen
value of .
Comparisons thus far have been performed on
subsamples whose observations were independent.
That is, DIFFERENT observations made up each
subsample such as frostbelt and sunbelt cities.
Another application of the t-test involves the SAME
sample measured at two different points in time. The
classic example is BEFORE and AFTER observations
on subjects in an experiment. Here the two sets of
observations are RELATED rather than independent.
These are called paired samples. Once again, a
different type of t-test must be used.
Suppose that we have a random sample of five
students from this class and that we want to test the
hypothesis that the class as a whole (the universe)
performed differently on the second examination
compared with the first. Since we do not know exactly
HOW the two scores differed (i.e., which was better
than the other), our alternate hypothesis commits us to
a two-tailed test. The null hypothesis is that the class
performed the same on both midterms. Our data
consist of Midterm One and Midterm Two scores for
each student. The independent-sample t-test is
inappropriate.
=========================================
_
_
_
Student Exam 1 Exam 2 D D (D – D)
(D - D)2
-----------------------------------------------------------------------1
2
3
4
5
92
88
81
72
50
89
70
75
67
35
3
18
6
5
15
9.4 - 6.4
9.4 8.6
9.4 - 3.4
9.4 - 4.4
9.4 5.6
40.96
73.96
11.56
19.36
31.36
----------------------------------------------------------------------- = 47
 = 177.20
The appropriate t-test is
D 
t 
ˆ D
To estimate the standard error of the paired differences,
we must first calculate the standard deviation for this
sample. It is, as before when we discussed univariate
statistics, the square root of the sum of the deviations
squared divided by the number of degrees of freedom
(here, D is used instead of Y to denote DIFFERENCES
between scores rather than the scores themselves).
 D  D 
2
sD 
N 1
In the present example, N = 5, the mean difference is
9.4 (i.e., 47 / 5 = 9.4), and the sum of the deviations
squared (the differences between the midterm score
differences and the mean difference) is 177.20. Thus,
the sample standard deviation is obtained as follows:
sD 
177.20
4
sD  44.30
sD  6.656
As before, we use the value of the sample standard
deviation (i.e., 6.656) to estimate the value of the
standard error (the standard deviation of the sampling
distribution of mean paired score differences). It is—
again—the sample standard deviation divided by the
square root of sample size, or
̂ D
ˆ D
sD

N
6.656

5
ˆ D 
6.656
2.236
ˆ D  2.977
Now we can calculate the value of the t-statistic and
make the usual hypothesis test by comparing t with the
critical values of t. Let's assume that alpha is 0.05. We
have 4 degrees of freedom. Thus, in Appendix 2
(p. 543) we find the critical values for a two-tailed test to
be  2.776. The value of t is:
D
t
ˆ D
Under the null hypothesis,  = 0.0.
9.4  0.0
t 
2.977
t  3.158
Since 3.158 is GREATER than the critical value, + 2.776,
we REJECT the null hypothesis at the 0.05 level and
infer that there is a statistically significant difference in
scores between the first and second midterm. Our
sample data suggest that in general scores went down
on the second exam compared to the first.
The SAS Procedure for Paired
Sample t-tests
libname new 'a:\';
libname library 'a:\';
options nonumber nodate ps=66;
data new.scores;
input student exam1 exam2;
diffrnce = exam1-exam2;
cards;
1 92 89
2 88 70
3 81 75
4 72 67
5 50 35
;
The SAS Procedure for Paired
Sample t-tests (continued)
proc print data=new.scores;
var _all_;
title1 'A Paired-Sample T-Test';
title2 'Values in SCORES.SD2';
title3 'PPD 404';
proc means data=new.scores n mean stderr
t prt;
var diffrnce;
title1 'A Paired-Sample T-Test';
title2 'Output';
title3 'PPD 404';
run;
A Paired-Sample T-Test
Values in SCORES.SD2
PPD 404
OBS
1
2
3
4
5
STUDENT
1
2
3
4
5
EXAM1
92
88
81
72
50
EXAM2
89
70
75
67
35
DIFFRNCE
3
18
6
5
15
A Paired Sample T-Test
Output
PPD 404
Analysis Variable: DIFFRNCE
N
Mean
Std Error
T Prob>|T|
----------------------------------------5
9.400
2.9765752 3.157
0.0343
-----------------------------------------