* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download note01: the free vibrations of physical systems
Dynamical system wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Seismic communication wikipedia , lookup
Center of mass wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Virtual work wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Thermodynamic system wikipedia , lookup
Seismometer wikipedia , lookup
Hooke's law wikipedia , lookup
Routhian mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Equations of motion wikipedia , lookup
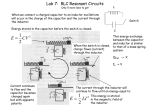
NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS NOTE: THERE ARE SPACES IN THE NOTE TO INSERT DIAGRAMS. The Free Vibrations of Physical Systems: (i) (ii) (iii) Mass-Spring The Simple Pendulum The LC circuit (i) The Mass – Spring System: (a) Horizontal mass-spring system: This system consists of a mass-less spring of spring constant 𝑘 attached to a body of mass m with one degree of freedom, given by the coordinate 𝑥, which represents the displacement of the body from the equilibrium position, i.e., the position of the body when the spring has its natural length. The equilibrium position of the body is then 𝑥 = 0. When the spring is deformed (stretched or compressed), the body experiences a force that is directly proportional to the amount by which the spring is deformed and the force is always directed opposite to the displacement of the body from its equilibrium position. This means that the force exerted by the spring is simple-harmonic and so when the mass is displaced by a certain amount and then released, the mass-spring system executes simple harmonic motion. The unit vector in the positive 𝑥-direction is denoted by 𝑖̂. The unit vector in the direction of the spring force is given by 𝐹⃗ … … … … … … … … … … … … … … (1) 𝐹 As shown in the diagram, the force exerted by the spring 𝐹⃗ is directed opposite to 𝑖.̂ So, 𝐹⃗ = −𝑖̂ … … … … … … … … … … … … … … (2) 𝐹 Or, 𝐹⃗ = −𝐹𝑖̂ … … … … … … … … … … … … . . (3) But 𝐹 = 𝑘𝑥, so that equation (3) becomes 1 NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS 𝐹⃗ = −𝑘𝑥𝑖̂ … … … … … … … … … . . (4) By Newton’s second law, 𝐹⃗ = 𝑚𝑎⃗, where 𝑚 is the mass of the body. So, from equation(4) we have 𝑎⃗ = − 𝑘𝑥 𝑖̂ … … … … … … … . . (5) 𝑚 Now, 𝑎⃗ = 𝑎𝑥 𝑖̂ + 𝑎𝑦 𝑗̂ + 𝑎𝑧 𝑘̂. Since the spring force is directed along the 𝑥-axis only, it follows that 𝑎𝑦 = 𝑎𝑧 = 0. So we have, from equation (5), 𝑎𝑥 𝑖̂ = − 𝑘𝑥 𝑖̂ 𝑚 Or 𝑎𝑥 = 𝑑2 𝑥 𝑘 = − 𝑥 … … … … … … … … . . (6) 2 𝑑𝑡 𝑚 Or 𝑑2 𝑥 𝑘 + 𝑥 = 0 … … … … … … … . (7) 𝑑𝑡 2 𝑚 This is the equation of simple harmonic equation in one dimension, i.e., for a system with one degree of freedom. (b) The Vertical Spring This system consists of a mass-less spring attached to a body of mass m with one degree of freedom, given by the coordinate 𝑦, which represents the displacement of the body from the equilibrium position, i.e., the position of the body when the spring is elongated by an amount 𝛥𝑙 due to the weight of the body. 2 NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS The unit vector in the positive 𝑦-direction is denoted by 𝑗̂. The forces acting on the body in ⃗⃗⃗⃗ of the body and the spring force 𝐹⃗ due to the equilibrium position are the weight 𝑊 elongation by 𝛥𝑙 of the spring. Since the body is in equilibrium, ⃗⃗⃗⃗ = ⃗0⃗ … … … … … … … … … . . (8) 𝐹⃗ + 𝑊 ⃗⃗⃗⃗ is The unit vector in the direction of 𝑊 ⃗⃗⃗⃗ 𝑊 = 𝑗̂ 𝑊 And the unit vector in the direction of 𝐹⃗ is 𝐹⃗ = −𝑗̂ 𝐹 Combining the above two equations we have ⃗⃗⃗⃗ 𝐹⃗ 𝑊 =− 𝐹 𝑊 Or 𝐹⃗ = − 𝐹 ⃗⃗⃗⃗ … … … … … … … . . (9) 𝑊 𝑊 From equations (8), (9) ⃗⃗⃗⃗ (1 − 𝑊 𝐹 ⃗⃗ )=0 𝑊 Or (1 − 𝐹 )=0 𝑊 Or 𝐹=𝑊 So we have the equation for the equilibrium position which is 𝑘𝜟𝒍 = 𝒎𝒈 … … … … … … … … . . (𝟏𝟎) When the body is displaced from its equilibrium position and then released it experiences the gravitational force and the spring force whose magnitude is directly proportional to the deformation of the spring and always directed opposite to the displacement of the body from its equilibrium position. Let the displacement of the body from the equilibrium position be 𝑦. Then, the forces acting ⃗⃗⃗⃗ and the force exerted by the on the body at this position are the weight of the body 𝑊 spring 𝐹⃗ . Since the body is not in the equilibrium position, the magnitude of the spring force is more than the magnitude of the weight of the body and so ⃗⃗⃗⃗ ≠ ⃗0⃗ 𝐹⃗ + 𝑊 And by Newton’s second law, ⃗⃗⃗⃗ = 𝑚𝑎⃗ … … … … … … … (11) 𝐹⃗ + 𝑊 ⃗⃗⃗⃗ is The unit vector in the direction of 𝑊 3 NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS ⃗⃗⃗⃗ 𝑊 = 𝑗̂ 𝑊 4 And the unit vector in the direction of 𝐹⃗ is 𝐹⃗ = −𝑗̂ 𝐹 Inserting the above equations in equation (11) we have, −𝐹𝑗̂ + 𝑊𝑗̂ = 𝑚𝑎⃗ … … … … … … … . (12) Now, 𝑎⃗ = 𝑎𝑥 𝑖̂ + 𝑎𝑦 𝑗̂ + 𝑎𝑧 𝑘̂. Since the forces are directed along the 𝑦-axis only, it follows that 𝑎𝑥 = 𝑎𝑧 = 0. Equation (12) becomes, −𝐹𝑗̂ + 𝑊𝑗̂ = 𝑚𝑎𝑦 𝑗̂ Or −𝐹 + 𝑊 = 𝑚𝑎𝑦 𝑜𝑟 −𝑘(𝛥𝑙 + 𝑦) + 𝑚𝑔 = 𝑚𝑎𝑦 … … … … … … … . (13) Using equation (10) in the above equation, we get, −𝑘𝑦 = 𝑚𝑎𝑦 = 𝑚 𝑑2 𝑦 𝑑𝑡 2 Or 𝑑2 𝑦 + 𝑘𝑦 = 0 … … … … … … … . (14) 𝑑𝑡 2 Which is the equation of simple harmonic motion. 𝑚 (ii) The Simple Pendulum A simple pendulum consists of a bob (treated as a point mass) of mass 𝑚 suspended from a fixed frictionless point O by an inextensible thread of length 𝑙. When the bob is drawn to one side and released, the bob executes to and fro motion. The axis of rotation (call it the 𝑧-axis) of the bob is a line that passes through the fixed point and perpendicular to the 𝑥𝑦 –plane (i.e. the plane of the paper). Let the angle 𝜃 denote the angle which the string makes with the vertical. Since the bob rotates about an axis of rotation as it executes the to and fro motion, we can calculate the angular velocity, angular acceleration, angular momentum and torque about O. NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS Suppose at time t, the velocity of the bob of the pendulum is 𝑣⃗. Then the angular momentum ⃗⃗⃗⃗ and the about O is 𝐿⃗⃗ = 𝑙⃗ × 𝑚𝑣⃗. The forces acting on the bob of the pendulum are its weight 𝑊 ⃗⃗. The torque due to these forces about O are 𝑙⃗ × 𝑊 ⃗⃗⃗⃗ and 𝑙⃗ × 𝑇 ⃗⃗. However tension on the string 𝑇 ⃗⃗. So the net torque about O is 𝜏⃗ = 𝑙⃗ × ⃗⃗ passes through O and so 𝑙⃗ × 𝑇 ⃗⃗ = 0 the line of action of 𝑇 ⃗⃗⃗⃗ . 𝑊 Referring to the diagram and using the property of the cross product(the right hand rule), we see that 𝐿⃗⃗ is along the positive direction of 𝑧-axis(out of the plane of the paper and along the unit vector 𝑧̂ ), whereas 𝜏⃗ is along the negative direction of 𝑧-axis (into the plane of the paper and opposite to 𝑧̂ ). So, 𝐿⃗⃗ = 𝑧̂ 𝐿 And 𝜏⃗ = −𝑧̂ 𝜏 Since 𝑙⃗ is perpendicular to 𝑣⃗, it follows that 𝐿 = 𝑙𝑚𝑣 = 𝑙𝑚𝝎𝒍 = 𝒎𝝎𝒍𝟐 and 𝝉 = 𝒎𝒈𝒍 𝐬𝐢𝐧 𝜽. From the above equations we have 𝐿⃗⃗ = 𝐿𝑧̂ … … … … … … (15) 𝑎𝑛𝑑 𝜏⃗ = −𝜏𝑧̂ … … … … … … … . (16) From the theory of rigid body dynamics 𝜏⃗ = 𝑑𝐿⃗⃗ … … … … … … … … … . . (17) 𝑑𝑡 From equations (15), (16), (17), 𝜏𝑧̂ = − 𝑑 (𝐿𝑧̂ ) 𝑑𝑡 or 𝜏=− 𝑑 𝐿 𝑑𝑡 Or 𝑚𝑔𝑙 sin 𝜃 = − 𝑑 (𝑚𝜔𝑙 2 ) 𝑑𝑡 Or 𝑑𝜔 𝑔 = − sin 𝜃 𝑑𝑡 𝑙 5 NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS Or 𝑑2 𝜃 𝑔 = − sin 𝜃 𝑑𝑡 2 𝑙 If the angle 𝜃 is much less than 1 radian, sin 𝜃 ≅ 𝜃. The above equation becomes 𝑑2 𝜃 𝑔 + 𝜃 = 0 … … … … … … … … (18) 𝑑𝑡 2 𝑙 So for angles much less than one radian the to and fro motion of the pendulum is simple harmonic in nature. (iii) The LC circuit The capacitor 𝐶 is assumed to be charged to a value 𝑞0 at time 𝑡=0. The capacitor is then connected in parallel to an inductor 𝐿. The charge on the capacitor decreases and the current increases so that electrical energy in the capacitor is transferred to magnetic energy in the inductor. The current at time 𝑡 is 𝑖=− 𝑑𝑞 … … … … … … … … … … … … … . . (1) 𝑑𝑡 The negative sign accounts for the fact that rate of change of charge in the capacitor is negative but current is positive. Positive work is done by the capacitor and negative work by the inductor. Assuming no loss or gain in the total energy, Work done by capacitor + Work done by inductor = 0 ....................................(2) Let at time 𝑡=𝑡 the charge on the capacitor be 𝑞. The work done by the capacitor as the charge falls from 𝑞0 to 𝑞 is given by 𝑞 𝑞 𝑡 ∫ 𝑣(−𝑑𝑞) = − ∫ 𝑣𝑑𝑞 = ∫ 𝑣𝑖𝑑𝑡 … … … … … … . (3) 𝑞0 𝑞0 0 The work done by the inductor from 𝑡=0 to 𝑡=𝑡 is given by 𝑡 ∫ (−𝐿 0 𝑑𝑖 ) 𝑖𝑑𝑡 … … … … … … … … … (4) 𝑑𝑡 6 NOTE01: THE FREE VIBRATIONS OF PHYSICAL SYSTEMS From equations (2), (3), (4) we have 𝑡 7 𝑡 𝑑𝑖 ∫ 𝑣𝑖𝑑𝑡 = ∫ (𝐿 ) 𝑖𝑑𝑡 𝑑𝑡 0 0 Or 𝑣=𝐿 𝑑𝑖 … … … … … … … … (5) 𝑑𝑡 Now, 𝑣= 𝑞 𝐶 𝑎𝑛𝑑 𝑖=− 𝑑𝑖 𝑑𝑡 So equation (5) becomes 𝑞 𝑑 𝑑𝑖 = 𝐿 (− ) 𝐶 𝑑𝑡 𝑑𝑡 Or 𝑑2 𝑞 1 + 𝑞 = 0 … … … … … … … … … (6) 2 𝑑𝑡 𝐿𝐶 Clearly the charge on the capacitor behaves simple harmonically. This shows that the LC circuit behaves as an electrical oscillator. END OF NOTE01