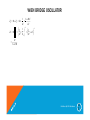* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Oscillators
Cavity magnetron wikipedia , lookup
Stage monitor system wikipedia , lookup
Alternating current wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Buck converter wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Chirp spectrum wikipedia , lookup
Utility frequency wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
Negative feedback wikipedia , lookup
Time-to-digital converter wikipedia , lookup
Crystal oscillator wikipedia , lookup
Phase-locked loop wikipedia , lookup
1
Objectives
• Define the basic oscillator circuit
• Identify elements of feedback in the oscillator
• Identify the conditions for oscillation to occur
• Identify input and output characteristics
• Identify common uses of the oscillator
Oscillators By S.M.Mehzabeen
2
Word Wall
• Oscillation: an effect that repeatedly and regularly
fluctuates about a mean value
• Oscillator: circuit that produces oscillation
• Characteristics: frequency, amplitude, distortion,
wave-shape, stability
Oscillators By S.M.Mehzabeen
3
Oscillator
In our daily life
– Digital watches, Invertors, Radios , T.V, Computers, Fans, Metal
Detectors, Electronic Bells and lots more
Pendulum of a clock.
– If you push on a pendulum to start it swinging, it will oscillate at
some frequency - it will swing back and forth a certain number
of times per second.
– The length of the pendulum controls the frequency.
– In pendulum potential energy is converted in kinetic energy
Oscillators By S.M.Mehzabeen
4
Overview of the Oscillator
• One of the basic building blocks of electronics
• Input is a direct current (DC) power source
• Output is alternating current (AC)
• Can generate sub-audible frequencies or very high
frequencies
• Most oscillators are amplifiers with feedback
Oscillators By S.M.Mehzabeen
5
Amplifiers as Oscillators?
• Most amplifiers will oscillate when conditions are correct
Example: Too high of a volume on public address system
= loud noise and squeals that are the result of acoustic
waves traveling from the speakers to the microphone
• The result is oscillation
Oscillators By S.M.Mehzabeen
6
Electrical Feedback
• Practical oscillators use electrical feedback to produce
oscillation
• Feedback circuits use resistors, capacitors, coils, or
transformers to connect a portion of the output signal back to
the input of the amplifier
Oscillators By S.M.Mehzabeen
7
Feedback and Amplifier Gain
Conditions for Oscillation
Feedback alone does not promise oscillation
There is always some loss in the feedback circuit
Amplifier gain must be greater than this loss
Feedback must be in-phase
Oscillators By S.M.Mehzabeen
8
In-phase Feedback
• In-phase feedback is also called regenerative feedback
or positive feedback
• When the original amplifier input and output signals are not
in-phase, the feedback circuit is used to reverse the phase
Oscillators By S.M.Mehzabeen
9
Input Characteristics
• Steady source of direct current (DC)
• In many applications, the DC source requires a filter
Oscillators By S.M.Mehzabeen
10
Output Characteristics
• Amplitude
• Frequency
• Waveform type
• Stability
• On some oscillators, the capability to change frequency
Oscillators By S.M.Mehzabeen
11
Oscillator Amplitude
• Usually determined by the gain available from the
amplifier
• Supply voltage and circuit losses affect amplitude
Oscillators By S.M.Mehzabeen
12
Oscillator Frequency
• Frequency of operation is normally determined by the
feedback circuit
• Common feedback circuits used to determine oscillator
frequency include:
– crystals
– resistor and capacitor networks (RC)
– coil and capacitor networks (LC) {tank circuit}
Oscillators By S.M.Mehzabeen
13
Waveform Type
• Generally, determined by:
– Feedback circuitry
– Output filter circuitry
– Amplifier gain, or
– Changes to input voltage
• May be sinusoidal (sine wave), square wave, or triangular
wave
Oscillators By S.M.Mehzabeen
14
Oscillator Stability
• Sometimes referred to as a stable oscillator
• Source of a signal with consistent amplitude
• Source of a signal with consistent frequency
Oscillators By S.M.Mehzabeen
15
Ability to Change Frequency
• Oscillators sometimes have the ability to change
frequencies
• Crystal oscillator frequency is controlled by changing the
crystal
– Crystals are usually cut from quartz to generate a
specified frequency when operating
Oscillators By S.M.Mehzabeen
16
Typical Uses of the Oscillator
• Radio and
television stations
require oscillators
to develop the
basic signal to
transmit their
information
Oscillators By S.M.Mehzabeen
17
Typical Uses of the Oscillator
• Cell
phones, electronic
keyboards,
and remote
controls use oscillators to
produce
the required
frequencies for operation
Oscillators By S.M.Mehzabeen
18
Typical Uses of the Oscillator
• Digital
devices
such as
computers, watches,
calculators, and iPods all
oscillators to
require
generate
the rectangular
waveform
required for
operation
Oscillators By S.M.Mehzabeen
19
Typical Uses of the Oscillator
• Variable oscillators, known
as signal generators, are
to generate
used
frequencies and waveforms
needed for troubleshooting
and the testing of electronic
equipment
Oscillators By S.M.Mehzabeen
20
Need of an Oscillator
• An oscillator circuit is capable of producing ac voltage of
desired frequency and waveshape.
• To test performance of electronic circuits, it is called
signal generator.
• It can produce square, pulse, triangular, or sawtooth
waveshape.
Oscillators By S.M.Mehzabeen
21
Need of an Oscillator
• High frequency oscillator are used in broadcasting.
• Microwave oven uses an oscillator.
• Used for induction heating and dielectric heating.
• Oscillators are circuits
that generate periodic
signals.
Oscillators By S.M.Mehzabeen
22
Need of an Oscillator
• An oscillator converts DC power from power supply to AC
signals power spontaneously – without the need for an AC
input source (Note: Amplifiers convert DC power into AC
output power only if an external AC input signal is present.)
• There are several approaches to design of oscillator circuits.
The approach to be discussed is related to the feedback
using amplifiers.
Oscillators By S.M.Mehzabeen
23
Need of an Oscillator
• A frequency-selective feedback path around an
amplifier is placed to return part of the output signal
to the amplifier input, which results in a circuit called
a linear oscillator that produces an approximately
sinusoidal output.
• Under proper conditions, the signal returned by the feedback
network has exactly the correct amplitude and phase needed to
sustain the output signal.
Oscillators By S.M.Mehzabeen
24
Types of Oscillators
•
Sinusoidal or non-sinusoidal.
•
An oscillator generating square wave or a pulse
train is called multivibrator :
1. Bistable multivibrator (Flip-Flop Circuit).
2. Monostable multivibrator.
3. Astable multivibrator (Free-running).
Oscillators By S.M.Mehzabeen
25
Types of Oscillators
•
Depending upon type of feedback, we have
1.
Tuned Circuit (LC) oscillators.
2.
RC oscillators, and
3.
Crystal oscillators.
Oscillators By S.M.Mehzabeen
26
Using Positive Feedback
The gain with positive feedback is given as
• By making 1 – Aβ = 0, or Aβ = 1, we get gain as infinity.
• This condition (Aβ = 1) is known as Barkhausen Criterion of oscillations.
• It means you get output without any input !
Oscillators By S.M.Mehzabeen
27
How is it Possible ?
• Connecting point x to y, feedback voltage drives
the amplifier.
Oscillators By S.M.Mehzabeen
28
How is it Possible ?
• What happens to the output ?
• There are three possibilities.
Oscillators By S.M.Mehzabeen
29
Basic principles for oscillation
• An oscillator is an amplifier with positive feedback.
Ve Vs Vf (1)
Vf βVo (2)
Vo AVe A Vs V AVs βVo
f
(3)
Oscillators By S.M.Mehzabeen
30
Basic principles for oscillation
Vo AV e A Vs Vf
Vo AVs Aββ o
• The closed loop gain is:
A Vs βVo
1 Aβ Vo AVs
Vo
A
Af
Vs 1 Aβ
Oscillators By S.M.Mehzabeen
31
Basic principles for oscillation
• In general A and are functions of frequency and thus
may be written as;
Vo
As
A f s
s
Vs
1 As βs
• is known as loop gain
As βs
Oscillators By S.M.Mehzabeen
32
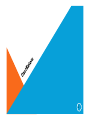
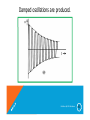
(1) If Aβ < 1, we get decaying of damped oscillations.
Oscillators By S.M.Mehzabeen
33
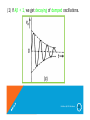
(2) If Aβ > 1, we get growing oscillations.
Oscillators By S.M.Mehzabeen
34
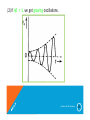
(3) If Aβ = 1, we get sustained oscillations. In this
case, the circuit supplies its own input signal.
Oscillators By S.M.Mehzabeen
35
Wherefrom comes the starting voltage ?
● Each resistor is a noise generator.
● The feedback network is a resonant circuit giving
maximum feedback voltage at frequency f0, providing
phase shift of 0° only at this frequency.
● The initial loop gain Aβ > 1.
● The oscillations build up only at this frequency.
● After the desired output is reached, Aβ reduces to unity.
Oscillators By S.M.Mehzabeen
36
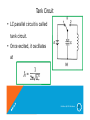
Tank Circuit
• LC parallel circuit is called
tank circuit.
• Once excited, it oscillates
at
Oscillators By S.M.Mehzabeen
37
Tank Circuit
The energy keeps oscillating between electric
potential energy and magnetic filed energy.
Oscillators By S.M.Mehzabeen
38
“OscillatorsarethecircuitswhichcovertsDC
VoltagefrombatterytoACVoltage”
– Without excitation input signal
A simple example
If you charge up the capacitor with
a battery and then insert the
inductor into the circuit, here's
what will happen
Oscillators By S.M.Mehzabeen
39
“OscillatorsarethecircuitswhichcovertsDC
VoltagefrombatterytoACVoltage”
• The capacitor will start to discharge through the
inductor. As it does, the inductor will create a
magnetic field
• Once the capacitor discharges, the inductor will try to
keep the current in the circuit moving, so it will
charge up the other plate of the capacitor.
Oscillators By S.M.Mehzabeen
40
“OscillatorsarethecircuitswhichcovertsDC
VoltagefrombatterytoACVoltage”
• Once the inductor's field collapses, the capacitor has
been recharged (but with the opposite polarity), so it
discharges again through the inductor
• Frequency will depend upon L and C
Oscillators By S.M.Mehzabeen
41
Tank Circuit
• When the tank circuit resonates, the circulating current
flows through L1 in series with L2. Hence the equivalent
inductance is
The feedback factor is
Oscillators By S.M.Mehzabeen
42
Damped oscillations are produced.
Oscillators By S.M.Mehzabeen
43
LC Oscillators
• Hartley oscillator.
• Colpitts oscillator.
• Clapp oscillator.
• Franklin oscillator
• Tuned Collector oscillator.
• Armstrong oscillator.
Oscillators By S.M.Mehzabeen
44
General Form of LC Oscillators
Oscillators By S.M.Mehzabeen
45
General Form of LC Oscillators - Description
• Amplifier –any active device EX:Vacuum
tube,Transistor,FET,Op-amp
• Z1,z2,z3 –determine the frequency of oscillation
• Z1,z2 serve as ac voltage divider for the output voltage
and feedback signal voltage across z1-feedback signal.
• 1,3 –input terminals.
• 2,3-output terminals.
Oscillators By S.M.Mehzabeen
46
General Form of LC Oscillators
Z’=z1 II h ie =
ZL =z’ +z3 II z2
Z L = II z2
Z L = + II
Oscillators By S.M.Mehzabeen
47
General Form of LC Oscillators
Vo = - I1(Z1+Z3) = -I1
vf =- I1 Z1 = - I1
vf=
β ==
Av = ZL
Oscillators By S.M.Mehzabeen
48
General Form of LC Oscillators
Av β =1
=1
General Equation of LC Oscillator:
hie (z1+z2+z3) +z1z2 (1+hfe)z1z3 =0
Oscillators By S.M.Mehzabeen
49
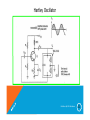
Hartley Oscillator
• Note that in the collector-tuned circuit, two inductor
coils are used.
• One end of these coils is grounded.
•
If we make the tickler coil an integral part of the circuit, we get Hartley Oscillator.
Oscillators By S.M.Mehzabeen
50
Hartley Oscillator
• LC oscillator
• Two inductive reactances
• One capacitive reactance in its feedback network.
Oscillators By S.M.Mehzabeen
51
Hartley Oscillator
Oscillators By S.M.Mehzabeen
52
Circuit Description
Amplifierstage:
1.Transistor –Active device in Common emitter
Configuration.
2.R1 and R2 biasing resistors.
3.RE-Biasing emitter resistance
4.CE-Emitter bypass capacitors.
Oscillators By S.M.Mehzabeen
53
Circuit Description
5.CC1 & CC2 are the coupling capacitors.
6.RFC-Radio frequency Choke(isolation b/w A.C & D.C)
Reactance value very high for high
frequencies.(open circuit)
Reactance value zero for D.C.Conditions.
Oscillators By S.M.Mehzabeen
54
Derivation of frequency of oscillation
Z1 =jwL1+jwM
z2 = jwL2 +jwM
z3=
General Equation of LC Oscillator:
hie (z1+z2+z3) +z1z2 (1+hfe)z1z3 =0
Oscillators By S.M.Mehzabeen
55
Derivation of frequency of oscillation
hie ( jwL1+ jwM+ jwL2 + jwM - )+
jwhie (L1 + L2 +2M – ) –(W2
Oscillators By S.M.Mehzabeen
56
Derivation of frequency of oscillation
Equating Imaginary part = 0
L1+L2+2M =
Oscillators By S.M.Mehzabeen
57
Derivation of frequency of oscillation
Equating Real part = 0
Oscillators By S.M.Mehzabeen
58
Derivation of frequency of oscillation
hfe L2 + hfe M –L1 –M = 0
Oscillators By S.M.Mehzabeen
59
Colpitts Oscillator
• An excellent circuit.
• LC Oscillator
• Two Capacitive Reactance
• One Inductive Reactance In The Feedback Network.
• Same As A Hartley Oscillator Except The Tank Circuit.
• Widely used in commercial signal generators.
Oscillators By S.M.Mehzabeen
60
Colpitts Oscillator
Oscillators By S.M.Mehzabeen
61
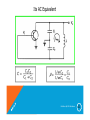
Its AC Equivalent
Oscillators By S.M.Mehzabeen
62
Circuit Description
Amplifierstage:
1.Transistor –Active device in Common emitter
Configuration.
2.R1 and R2 biasing resistors.
3.RE-Biasing emitter resistance
4.CE-Emitter bypass capacitors.
Oscillators By S.M.Mehzabeen
63
Circuit Description
5.CC1 & CC2 are the coupling capacitors.
6.RFC-Radio frequency Choke(isolation b/w A.C & D.C)
Reactance value very high for high frequencies.(open
circuit)
Reactance value zero for D.C.Conditions.
Oscillators By S.M.Mehzabeen
64
DERIVATION OF FREQUENCY OF OSCILLATION
Z1 =
Z2 =
Z3 = jwL
• General Equation of LC Oscillator:
hie (z1+z2+z3 ) +z1z2 (1+hfe)z1z3 =0
Oscillators By S.M.Mehzabeen
65
DERIVATION OF FREQUENCY OF OSCILLATION
• General Equation of LC Oscillator:
hie (z1+z2+z3 ) +z1z2 (1+hfe)z1z3 =0
hie ( + = 0
j hie ( + -wL ) +( –
Oscillators By S.M.Mehzabeen
66
DERIVATION OF FREQUENCY OF OSCILLATION
• Equating Imaginary part = 0
+ = wL
=wL
=w2 L
w2 =
fr =
=
fr =
Oscillators By S.M.Mehzabeen
67
DERIVATION OF FREQUENCY OF OSCILLATION
• Equating Real part = 0
=
= =c2 L
hfe = - 1
= w2c2L
1+hfe =
hfe =
Oscillators By S.M.Mehzabeen
68
Oscillators By S.M.Mehzabeen
69
Solution :
Oscillators By S.M.Mehzabeen
70
Oscillators By S.M.Mehzabeen
71
CLAPP OSCILLATOR
• To Achieve Frequency Stability Colpitts Oscillator Circuit
Slightly Changed-clapp Osc
• Addition Of One More Capacitor C3 Is Introduced In
Series With The Inductance.
KEY POINT:
• C3 Much More Smaller Than C1 And C2.
Oscillators By S.M.Mehzabeen
72
CLAPP OSCILLATOR - CIRCUIT DIAGRAM
Oscillators By S.M.Mehzabeen
73
Circuit Description
Amplifierstage:
1.Transistor –Active device in Common emitter
Configuration.
2.R1 and R2 biasing resistors.
3.RE-Biasing emitter resistance
4.CE-Emitter bypass capacitors.
Oscillators By S.M.Mehzabeen
74
Circuit Description
5.CC1 & CC2 are the coupling capacitors.
6.RFC-Radio frequency Choke(isolation b/w A.C & D.C)
Reactance value very high for high frequencies.(open
circuit)
Reactance value zero for D.C.Conditions.
Oscillators By S.M.Mehzabeen
75
Derivation of frequency of oscillation
• Provides improved stability
• Permits capacitive tuning of the oscillator if C3 is variable.
1
fr
2
1
Lc3
1
fr
2 L(
c1c2c3
)
c1c2 c1c3 c2c3
c1c2
c3
c1 c2
Oscillators By S.M.Mehzabeen
76
ADVANTAGES of Colpitts oscillation
• The frequency is stable and accurate.
• The good frequency stability.
• The stray capacitances have no effect on C3 which
decides the frequency.
• Keeping C3 variable, frequency can be varied in the
desired range.
Oscillators By S.M.Mehzabeen
77
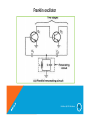
Franklin oscillator
• Two Transistor Stages With Some Common Terminal(emitter)
• Each Stage Provides 180 Phase Shift
• Both Stages Provides Amplification As Well As Phase
Inversion
• The Resonating Circuit Is Isolated From Active Device Path By
C1 And C2.
• Resonating Circuit Isolated From Input Of First Stage And
Output Of Second Stage.
Oscillators By S.M.Mehzabeen
78
Franklin oscillator
Oscillators By S.M.Mehzabeen
79
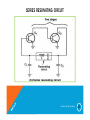
SERIES RESONATING CIRCUIT
Oscillators By S.M.Mehzabeen
80
PRACTICAL FRANKLIN OSCILLATOR CIRCUIT
Oscillators By S.M.Mehzabeen
81
Franklin oscillator - CIRCUIT DESCRIPTION
• Parallel Resonating Circuit Formed By L And C.
• Rb Coupling Resistance
• Rf Feedback Resistance.
• Attenuation Caused By These Two Decides Loop Gain
• Parallel Resonating Is Most Popular Than Series
Resonating Circuit.
Oscillators By S.M.Mehzabeen
82
DERIVATION OF FREQUENCY OF OSCILLATION
1
YL
Rs jLs
Yc jc
Rs jLs
YT 2
j C
2
2
Rs Ls
YT YL YC
Rs jLs
YT 2
j C
2
2
Rs Ls
Rs
jLs
YT 2
2
jC
2
2
2
2
Rs Ls
Rs Ls
=
1
j C
Rs jLs
Oscillators By S.M.Mehzabeen
83
DERIVATION OF FREQUENCY OF OSCILLATION
• Equate Imaginary Part to zero:
Ls
C 0
2
2
2
Rs Ls
Ls 2 2
Ls
Rs 2
c
Rs2
1
2
LsC Ls
Ls
Rs 2 2 Ls 2
c
1
Rs 2
2
LsC Ls
2
2
1
1
Rs
(
f
2)
LsC Ls
2
Oscillators By S.M.Mehzabeen
84
DERIVATION OF FREQUENCY OF OSCILLATION
f
1
2
LsC
Rs 2
2
Ls
1
• The impedance at resonance condition is
determined from the real part.
1
zr
Yr
Rs 2 2 Ls 2
2 Ls2
1
zr
Rs
Yr
Rs
Rs
Oscillators By S.M.Mehzabeen
85
DERIVATION OF FREQUENCY OF OSCILLATION
• Substituting value 2
Ls
zr
CRs
Rs 2
Ls 1
zr Rs
(
2 )
Rs LsC Ls
Ls
zr Rs
Rs
CRs
Ls
zr
CRs
2
Oscillators By S.M.Mehzabeen
86
FREQUENCY RANGE
• 100MHZ TO 3 GHZ
Oscillators By S.M.Mehzabeen
87
APPLICATION
• RF Oscillator
• Precision Frequency Meter-used For The Measurement Of
Frequency
Oscillators By S.M.Mehzabeen
88
ARMSTRONG OSCILLATOR
Oscillators By S.M.Mehzabeen
89
TICKLER OSCILLATOR
• Small Secondary Winding Is Called Tickler Coil.
• Hence Another Name Tickler Oscillator.
Oscillators By S.M.Mehzabeen
90
CIRCUIT DESCRIPTION
• LC Oscillator.
• Employs Transformer Action.
• Primary Acts As A Inductor(L)
• Voltage Across The Secondary Used As A Feedback.
• Biasing Point Selected By R1,R2,RE.
Oscillators By S.M.Mehzabeen
91
CIRCUIT DESCRIPTION
• C1 And C2 Coupling Capacitors.
• C3 Emitter Bypass Capacitor.
• Feedback Signal Applied To The Base.(Q)
• Transformer 180 Phase Shift .Transistor Q 180
Phaseshift.
• Overall Phase Shift 360 Satisfies Barkhausen
Criterion.
Oscillators By S.M.Mehzabeen
92
FREQUENCY OF OSCILLATION
• The Sustained Oscillation Depends On Inductance(l) And
Capacitance(C)
Oscillators By S.M.Mehzabeen
93
DRAWBACKS
• Rarely Used.
• Compared To Other LC Oscillator.
• Transformer Used
• Circuit Costlier And Bulkier.
Oscillators By S.M.Mehzabeen
94
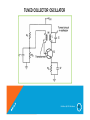
TUNED COLLECTOR OSCILLATOR
Oscillators By S.M.Mehzabeen
95
WHY?
• The Tuned Circuit Is Placed In The Collector Of The
Transistor.
• Hence Called Tuned Collector Oscillator.
Oscillators By S.M.Mehzabeen
96
CIRCUIT DESCRIPTION
• LC Oscillator.
• Employs Transformer Action.
• Primary Acts As A Inductor(L)
• Voltage Across The Secondary Used As A Feedback.
• Biasing Point Selected By R1,R2,RE.
Oscillators By S.M.Mehzabeen
97
CIRCUIT DESCRIPTION
• Collector Drives The LC Resonating Circuit.
• Feedback Signal Induced From The Primary Applied To The
Base.(Q)
• Transformer 180 Phase Shift .Transistor Q 180 Phaseshift.
• Overall Phase Shift 360 Satisfies Barkhausen
Criterion.
Oscillators By S.M.Mehzabeen
98
FREQUENCY OF OSCILLATION
• The Sustained Oscillation Depends On Inductance(l) And
Capacitance(C)
Oscillators By S.M.Mehzabeen
99
DRAWBACKS
• Rarely Used.
• Compared To Other LC Oscillator.
• Transformer Used
• Circuit Costlier And Bulkier.
Oscillators By S.M.Mehzabeen
10
0
Oscillators By S.M.Mehzabeen
10
1
RC Oscillators
•
Three types :
1. RC Phase shift Oscillator.
2. Wein Bridge Oscillator.
3. Twin T Oscillator.
Oscillators By S.M.Mehzabeen
10
2
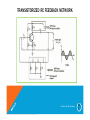
TRANSISTORIZED RC FEEDBACK NETWORK
Oscillators By S.M.Mehzabeen
10
3
RC FEEDBACK NETWORK
Oscillators By S.M.Mehzabeen
10
4
Derivation for RC phase shift oscillator.
Let c1 =c2=c3=c
R1=R2=R
R3+(Rth II Rin’)=R
Oscillators By S.M.Mehzabeen
10
5
Derivation for RC phase shift oscillator.
Oscillators By S.M.Mehzabeen
10
6
Derivation for RC phase shift oscillator.
Oscillators By S.M.Mehzabeen
10
7
Derivation for RC phase shift oscillator.
Oscillators By S.M.Mehzabeen
10
8
Derivation for RC phase shift oscillator.
Oscillators By S.M.Mehzabeen
10
9
Derivation for RC phase shift oscillator.
Oscillators By S.M.Mehzabeen
11
0
Advantages and Disadvantages of RC oscillator
Advantages
Disadvantages
• Doesn ’ t require any • Fixed frequency oscillator.
bulky
and expensive
inductors.
• Only one frequency fulfill
barkhausen criterion .
• Pure sine wave output is
possible.
Oscillators By S.M.Mehzabeen
11
1
Oscillators By S.M.Mehzabeen
11
2
Solution :
Oscillators By S.M.Mehzabeen
11
3
WIEN BRIDGE OSCILLATOR
Oscillators By S.M.Mehzabeen
11
4
WIEN BRIDGE OSCILLATOR
Z S R ZC R
1
1 sRC
sC
sC
1
1 1 1
sC
Z P R ZC
R ZC R
1
R
1 sCR
Oscillators By S.M.Mehzabeen
11
5
WIEN BRIDGE OSCILLATOR
Input Loading
1 1
Z1 Z P Z S
ZP Z S
1
sC
R1 sCR
1 sCR
R 1 sCR sCR (1 sCR)2
1
Output Loading
Z2 ZS R ZC
1 sRC
sC
Oscillators By S.M.Mehzabeen
11
6
Amplifier Gain
Ar
V 0 V 0 Vi
IS
Vi I S
To
get
V0
, we use
Vi
Vi V V I 1 R1
V0 R1 R 2
Vi
R1
Since
1
I 0,
I1 I 2
Vo
R1 R 2
and
Vo
R1 so
R1 R 2
R2
R1
Vi
Z 1 and
IS
V 0 Vi
R
Z 1 1 2
Vi I S
R1
R 1 sCR
where Z 1
sCR (1 sCR ) 2
Ar
so
R
R 1 sCR
Ar 1 2
R1 sCR (1 sCR ) 2
Oscillators By S.M.Mehzabeen
11
7
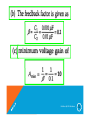
Feedback factor
f
Xf
Xo
If
Vo
1
ZS
sC
1 sRC
Oscillators By S.M.Mehzabeen
11
8
Oscillation Condition
Phase
of f A r equal to 180 o . It already
Then
need
R
is since
f Ar 0.
sCR
f A r 1 2
1
R1 sCR (1 sCR ) 2
only
Rewriting
f Ar 1
R2
sCR
R1 sCR (1 sCR ) 2
sCR
R
1 2
R
1
2
sCR s 2 C 2 R 2
sCR
1
R
sCR
R
1 2
1 2
2
2
2
R1 1 3 sCR s C R
R1
R
1
1 2
1
R
1 3 j CR
CR
Then imaginary
term 0 at
1
o
RC
Then, we can get
the
1
3 1 sCR
sCR
oscillatio n frequency
f Ar 1 by selecting
the resistors
R1 and
R2
appropriat ely using
R 1
1 2 1
R1 3
or
R2
2
R1
Oscillators By S.M.Mehzabeen
11
9
Loop gain
sC
Ar
1
sCR
f Ar
sC R2
R1 sCR
1
R1 sCR (1 sCR) 2
1 sCR
R
sCR
1 2
R1 sCR (1 sCR) 2
Gain with feedback is
Arf
Ar
1 f Ar
Oscillators By S.M.Mehzabeen
12
0
Advantages and Disadvantages of wien bridge oscillator
Advantages
Disadvantages
• It uses both positive and • More
negative
feedback, it
provides
better stability
and high over all gain.
• Frequency can be easily
components used
costlier.
• It cant generate very high
frequency.
adjusted by varying R or C
Oscillators By S.M.Mehzabeen
12
1
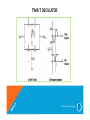
TWIN T OSCILLATOR
Oscillators By S.M.Mehzabeen
12
2
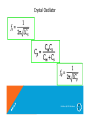
Crystal Oscillator
• The Piezoelectric Effect Quartz exhibits piezoelectric effect.
– When a changing mechanical stress is applied across the
crystal to cause it to vibrate, a voltage develops at the
frequency of mechanical vibration.
– Conversely, whenanacvoltageisappliedacrossthecrystal,it
vibratesatthefrequencyoftheappliedvoltage.Thegreatest
vibrationoccursatthecrystal'snaturalresonantfrequency.
– Which is determined by the physical dimensions and by the way
the crystal is cut.
Oscillators By S.M.Mehzabeen
12
3
Crystal Oscillator
Oscillators By S.M.Mehzabeen
12
4
Crystal Oscillator
• From equivalent circuit it is clear that it consists of series
as well as parallel resonant circuit
• At series resonance inductive reactance is equal to
capacitive reactance Cs
• At parallel resonance inductive reactance is equal to
capacitive reactance Cm
• So,crystal can be used in hartley or colpitts oscillator in
place of the tank circuit
Oscillators By S.M.Mehzabeen
12
5
Crystal Oscillator
Oscillators By S.M.Mehzabeen
12
6
Crystal Oscillator
• Used when accuracy and stability of fo is utmost
important.
• Where do you need such high stability of frequency of
oscillations ?
• Instead of an inductor, it uses a crystal of quartz,
tourmaline, or Rochelle salt.
Oscillators By S.M.Mehzabeen
12
7
Crystal Oscillator
• Piezoelectric effect.
• The crystal is suitably cut and then mounted between
two metallic plates.
• The fundamental frequency is given as
Oscillators By S.M.Mehzabeen
12
8
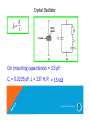
Crystal Oscillator
Cm (mounting capacitance) = 3.5 pF;
Cs = 0.0235 pF; L = 137 H; R = 15 kΩ
Oscillators By S.M.Mehzabeen
12
9
Crystal Oscillator
• Crystals have incredibly high Q.
• For the given values, Q = 5500.
• Q as high as 100 000 can be possible.
• An LC circuit has Q not greater than 100.
• The extremely high value of Q makes fo highly
stable.
Oscillators By S.M.Mehzabeen
13
0
Crystal Oscillator
Oscillators By S.M.Mehzabeen
13
1
Series and Parallel Resonance
• First, resonance occurs at fs for the series combination of
L and Cs.
• Above fs the series branch LCsR has inductive reactance.
• It then resonates at fp , with Cm.
• For this parallel resonance, equivalent series
capacitance is Cp.
Oscillators By S.M.Mehzabeen
13
2
Crystal Oscillator
Oscillators By S.M.Mehzabeen
13
3
Crystal Oscillator
• Normally, Cs is much smaller than Cm.
• Therefore, Cp is slightly less than Cs.
• Hence, the frequency fp is slightly greater than fs.
• The crystal is inductive only between the frequencies fs
and fp.
• The frequency of oscillation must lie between these
frequencies.
• Hence the stability.
Oscillators By S.M.Mehzabeen
13
4
The fo is between 411 kHz and 412 kHz.
Oscillators By S.M.Mehzabeen
13
5
Pierce Oscillator
• If we assume that the current through C1,2 is larger than
the collector current (high Q), then we see that the same
current flows through both capacitors. The voltage at the
input and output is therefore
vo I1
1
jC1
vi I1
1
jC2
vo
C
n 1
C2
vi
Oscillators By S.M.Mehzabeen
13
6
FACTORS AFFECTING THE FREQUENCY STABILITY
• Change in temperature affects –component values of the
tank circuit.
• Change in temperature affects active device parametres
inturn affect the frequency.
• Variation in the power supply the another factor affecting
the frequency.
• Changes in the load connected affect the effective
resistance of the tank circuit.
Oscillators By S.M.Mehzabeen
13
7
MODIFICATIONS FOR FREQUENCY STABILITY
• Enclosing the circuit in a constant temperature chamber.
• Maintaining constant voltage by using the zener diodes.
• Load effect is reduced by coupling the oscillator to the
load loosely
• Circuit having high input impedance and low output
impedance.
Oscillators By S.M.Mehzabeen
13
8
Variation of frequency with temperature.FOR
FREQUENCY STABILITY
• It is denoted by ‘S’.
Oscillators By S.M.Mehzabeen
13
9
Review
• Need of an Oscillator.
• Types of Oscillators.
• Using Positive Feedback.
• Barkhausen Criterion of Oscillations.
• Starting Voltage .
• Tank Circuit.
• Tuned Collector Oscillator.
Oscillators By S.M.Mehzabeen
14
0
Review
• Hartley Oscillator.
• Colpitts Oscillator.
• RC Phase Shift Oscillator.
• Wien Bridge Oscillator.
• Crystal Oscillator.
• Series and Parallel
Resonance
Oscillators By S.M.Mehzabeen
14
1