* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ASSESSING AND N. MITNE-284
Survey
Document related concepts
Transcript
ASSESSING THE RELIABILITY OF COMPONENTS
AND COMPLEX SUBSYSTEMS
MITNE-284
July, 1988
Prepared by:
N. Siu
T. Pagnoni
ASSESSING THE RELIABILITY OF COMPONENTS
AND COMPLEX SUBSYSTEMS
MITNE-284
July, 1988
Prepared by:
N. Siu
T. Pagnoni
Principal Investigator:
N. Siu
Department of Nuclear Engineering
Massachusetts Institute of Technology
Cambridge, Massachusetts 02139
Progress Report Prepared for:
Rockwell International Corporation
R. T. Lancet, Program Manager
Reactor Plant Safety/Reliability
ACKNOWLEDGEMENTS
This report is part of the MIT Department of Nuclear Engineering project
"Nuclear Power Design Innovation for the 1990's." The objective of this project is
to assess and explore promising technological avenues for enhancing the
attractiveness of the U.S. nuclear energy option.
Financial support for this study was provided by the Rocketdyne Division of
Rockwell International Corporation. The authors would like to acknowledge Bob
Lancet of Rockwell International for his support, and Anne Hudson for her
assistance in report preparation.
TABLE OF CONTENTS
Page
Section
Title
1.0
Introduction and Summary
1
1.1
1.2
1.3
Objectives
Background
Summary of Results
1
1
3
2.0
Overview of Approach
5
3.0
Check Valve Characterization
11
3.1
3.2
Check Valve Modeling
Check Valve Failure Data
11
13
4.0
Check Valve Analysis
19
4.1
4.2
4.3
4.3.1
4.3.2
4.3.3
Failure Mode Identification
Statistical Analysis of MCS Frequencies
Continuous Variable MCS Quantification
Independent Failure
Dependent Failures
Quantification
19
19
22
22
25
25
5.0
Concluding Remarks
35
6.0
References
37
Appendix
An Overview of First Order Reliability Analysis
A-1
LIST OF TABLES
Table
Title
Page
1
Check Valve Failure Data
14
2
Minimal Cut Sets for Swing Check Valve (Fail to Close)
30
3
Characteristic Parameters for rl(Ad| E)
31
4
Typical Values for Check Valve Wear Model Parameters
32
5
Sensitivity Analysis Results
33
LIST OF FIGURES
Figure
Title
Page
1
A Typical Swing Check Valve [8]
7
2
Hypothetical Relationship for Stud and Shaft Wear
8
3a
Conventional Fault Tree for Failure Example
9
3b
Shorthand Fault Tree for Continuous Variables
(Using CAND Gate)
9
4
Stress-Strength Model
10
5
Multivariable Failure Model
10
6
Regions of Flow-Induced Motion in Check Valves [16]
16
7
Distribution of Failure Types, Swing Check Valve
Fail-To-Open (FTO)
17
8
Distribution of Failure Types, Swing Check Valve
Fail-To-Close (FTC)
18
9
Fault Tree for Swing Check Valve Fail-To-Close
34
1. Introduction and Summary
1.1
Objectives
The reliability of a component (or a complex subsystem), the probability that
the component will function when demanded and for the duration of the mission, is
one of the key parameters to be considered when designing a new component for use
in a nuclear power plant safety system. In order to conduct the design optimization
process, formal tools for analyzing component reliability are required. These tools
must be capable of treating those characteristics unique to components (as opposed
to larger systems composed of components), and must be useful even when no
operational or test data are yet available.
The latter case, where the component is still in the design or construction
phase, is especially important to the expanded use of reliability analysis methods in
the design process. Without success/failure data, of course, the predictions even of
formal models will be subject to considerable uncertainty. However, they will show
the level of reliability and the principal contributors to failure expected based on the
current state of knowledge. Perhaps more importantly, they will also identify levels
of key parameters needed to assure a high level of reliability. For example, if
particular component assembly tolerances are identified as being critical to the
overall reliability, special attention can be paid to ensuring that these tolerances are
met.
This report identifies and, where necessary, develops tools useful for the
quantitative reliability modeling of components. These tools are intended for the
use of a designer, and are to be applicable even when developing an entirely new
design for which no directly applicable failure data are available. The initial area of
application is in the design of mechanical components; however, the methods
adopted should be general enough to handle a wide variety of cases.
Background
Formal methods have been developed to evaluate the reliability of systems
composed of components whose individual reliabilities can be estimated from
available data, and where the interactions between components are fairly limited
(e.g., [1,2]). However, methods to analyze the reliability of the components
themselves when data are not available have not received the same amount of
1.2
attention.
In a typical safety system reliability analysis, the hardware contribution to
1
component unreliability is quantified using two parameters: Qd, the unreliability on
demand, and A, the (assumed) constant failure rate of the component. The
hardware unreliability is then given by
Qd+(1-Qd)(1-e
Qh
Qd + A
where r is the system mission time.
Both Qd and A can be estimated from available failure and success data using
a variety of approaches. Bayesian methods are generally used when the amount of
data is fairly limited and when experts' opinions are employed to supplement the
data base [3].
More complex models than the Qd-A model can be used, of course. One
approach, not generally used in nuclear plant assessments but fairly widespread in
other industries, is to assume that the time-to-failure model is governed by a more
complex distribution, such as the Weibull, rather than an exponential distribution.
In the case of the Weibull, the single parameter A is replaced by two parameters a
and
#:
Qh
~
A(t)
=at-
(1.2)
d + JA(t)dt
where
Equations (1.1) and (1.2) are statistical models for component failure. They
quantify the likelihood of failure, but do not identify the failure mode, and,
therefore, do not indicate design options that can be taken to reduce the likelihood
of failure. To accomplish the latter objective, a more detailed model of the
component is required.
At first glance, the standard methods used to analyze system reliability (e.g.,
block diagrams and fault trees) should also be used to analyze component reliability,
since most power plant components can be considered as complex subsystems.
However, two characteristics of system designs which enable the effective use of
2
these methods are not shared by many components.
First, the performance of a standby safety system can usually be modeled in
terms of the success or failure of its constituent components. The question of how a
system will fail can be answered in terms of discrete combinations of component
failures. Thus, a particular swing check valve can be singled out as being a
dominant contributor to unreliability; improvements to increase system reliability
can be made by improving the valve or adding a redundant path. At the component
level, however, a discrete model may not be as useful. The check valve failure may
be due to a combination of continuously varying factors, such as the amount of wear
of the valve hinge, the amount of corrosion product build up in the valve body, and
so forth, all of which combine to cause overall failure. The failure of the component,
therefore, often cannot be resolved in terms of the success or failure of the
component's parts, but rather must be described in terms of continuous changes in
these parts and the interaction between the parts.
The second problem, related to the first, is that the current reliability analysis
methods for treating interactions between components are not tailored to treat the
interactions between component parts. In a standard system analysis, interactions
between components are usually limited in number and quite well defined. Cause
and effect relationships often are non-existent (e.g., the failure of one valve does not
cause the failure of another) or unimportant (e.g., loss of flow through a valve
causes pump failure through overheating, but the system is already failed due to loss
of flow). Correlation models for treating coupling between components exist (e.g.,
[4-6]), but are intended to model the more or less simultaneous failure of
components due to a single common cause. Compared with components in a
system, the parts in a component are often more tightly coupled. Changes in a part,
which, as indicated above, cannot always be modeled in terms of "success" or
"failure" of that part, affect the behavior of other parts; the combination of changes
in all of the parts leads to success or failure of the component.
1.3
Summary of Results
From the above discussion, it can be seen that current plant analysis methods
for determining reliability are not completely suited for analyzing components. This
report presents a potential approach for extending these methods.
The approach employs conventional reliability analysis tools (e.g., fault trees)
to identify component failure modes (see Section 2). Some of the failure modes
involve mechanical failure, and are treated by limited physical modeling of the
3
component. Structural reliability analysis methods developed in civil engineering
which deal explicitly with continuous systems, are applied when appropriate. A
computer code which implements these latter methods, called FORM [7], is useful in
this context. Other failure modes are treated using statistical techniques currently
used to analyze component failure frequencies.
To ensure a good degree of practicality and realism in the approach, the study
is conducted with reference to a particular example: the analysis of swing check
valve reliability. This is believed to be a good example because of the simple design
involved; a realistic analysis can be performed without becoming overwhelmed by
details. It is also a good example because failure data obtained from actual field
experience are available, therefore allowing a comparison of the relative importance
of the different failure modes.
The characteristics of swing check valves and available information on their
failure are outlined in Section 3. The latter information include predictions of
engineering models as well as field data. Information has also been obtained from
interviews with Professor P. Griffith, an expert on check valve behavior, and with
personnel familiar with the operation and failure of check valves in marine
propulsion applications.
The methodology discussed in Section 2 is applied to selected portions of the
check valve reliability analysis in Section 4. The purpose is not to actually quantify
check valve reliability, but rather to: a) show how this quantification can be
performed, given the available models and data, and b) to show how the
methodology is useful in identifying and quantifying the impact of critical design
parameters which can affect reliability.
Section 5 discusses the results of the analysis and how these results can be
applied to the design of new components and subsystems.
4
2. Overview of Approach
From the preceding discussion, component reliability models must treat
complex interactions between parts, interactions which are not naturally
represented using discrete logic diagrams. On the other hand, specific component
failure modes can generally be identified. The approach adopted, therefore, has
both continuous and discrete features.
The first step in the analysis is to construct a fault tree for the component.
As with any other fault tree, the objective is to identify all of the different
mechanisms that may cause failure; special care must be taken to ensure
completeness. Unlike conventional fault trees, the basic events for the tree may
include partial failures; a special AND gate the "CAND" gate, is introduced to show
that continuous combinations of different levels of degraded part performance can
lead to failure. While the CAND gate is an AND gate with respect to the logic
structure of the tree, it is not treated as a conventional (discrete) AND gate when
quantifying the likelihood of the gate's top event.
For example, consider a swing check valve where the combined wear of the
shaft and of the attaching stud (see Figure 1 [8]) can cause improper seating of the
gate. Consider a hypothetical relationship between the wear of the two parts and
failure (improper seating) as illustrated in Figure 2, a conventional fault tree for this
event is shown in Figure 3a. The corresponding tree which uses the shorthand
CAND notation is shown in Figure 3b.
The second part of the analysis is to quantify the likelihood of the fault tree
top event, i.e., to quantify the minimal cut sets of the tree. In some cases, the basic
event likelihoods are determined as in standard analyses (e.g., the frequency of
improper re-assembly following maintenance). In others, particularly those linked
by CAND gates, a methodology which can treat the interaction of continuous
variables is needed.
A direct treatment of continuous variables is suggested by the well-known
stress strength model [9]. Let a represent the "stress" on a particular part, and
let S represent that part's "strength" with respect to the stress. Let a be a random
variable with probability density function p (-) and let S be a fixed value (see
Figure 4). Then,
5
P{failure} = P{Stress > Strength}
=
(2.1)
PU(u)da
An extension of this method to more than one variable is immediately
suggested. Let X and Y be two governing random variables with joint density
function PXy(-, -), and define a region of failure RF as shown by the shaded area in
Figure 5. Then
P{failure} =
J
JPxy(x,y)dxdy
RF
(2.2)
Two practical problems keep the analysis from being entirely straightforward.
First, the key parameters (X and Y in this case), the joint density function, and the
failure region must be defined. Depending upon the particular problem, this may
not be an easy task; it is further addressed in the context of check valve analysis in
Section 4. Second, a very large amount of computation is required if several
variables, rather than just two, are needed to characterize component failure, or if
the parameters of the joint density function are themselves uncertain. Numerical
approximations to reduce the computational load have been considered extensively
by civil engineers. One approach is to linearize the boundaries of RF and to
transform the governing variables (e.g., X and Y) such that the transformed
variables (e.g., X' and Y') follow a multivariate normal distribution. This method,
called "First Order Reliability Analysis" [7,10-14], is discussed in the Appendix.
An application of this method to the swing check valve problem is discussed in
Section 4.
6
anti-rotation
gate
Figure 1: A typical swing check valve [8]
7
Stud
Wear
No Failure
Shaft Wear
Figure 2: Hypothetical Failure Relationship
for Stud and Shaft Wear
8
Figure 3a: Conventional Fault Tree for Failure Example
Figure 3b: Shorthand Fault Tree for Continuous Variables
(Using CAND Gate)
9
Survival
Stress
pdf
Failure
W=S
Stress
Figure 4: Stress-Strength Model
V
RF (f eil ure)
/
,
x
.
Figure 5: Multiveriable Failure Model
10
3. Check Valve Characterization
The problem of check valve reliability analysis is selected to provide a simple
area of application for the methodology. It should be noted that despite this
simplicity, check valve failures are often visible contributors to system
unavailability, and the analysis of these failures is therefore important.
A typical check valve design is shown in Figure 1 [8]. It can be seen that the
valve has only one moving assembly: the arm/gate assembly. Two failure modes of
importance are fail to close (FTC) and fail to open (FTO). The former can be
caused by improper seating of the gate on the valve seat which, in turn, can be
caused by a number of mechanisms. For example, shaft or hinge wear can lead to
vertical displacement of the gate and, therefore, improper seating of the gate.
Improper seating can also be caused by cocking of the gate, which may occur after
the securing nut is loosened.
In this section, physical models relevant to check valve degradation due to
hinge wear and due to gate tapping are briefly outlined and failure data from
nuclear power experience are described. The presentation in both cases is not
exhaustive; the objective is to indicate the kind of information available for existing
components and the failure modes likely to be experienced under realistic operating
conditions.
Check Valve Modeling
Reference 15 presents a number of mechanisms leading to the FTC mode
observed in nuclear power plants. Two particular failure initiators analyzed in some
3.1
detail are hinge wear, which may lead directly to improper seating or to jamming,
and gate tapping against the stop (see Figure 1), which may lead to failure of the
cotter pin, loosening of the nut, and eventual improper seating or jamming.
Hinge wear is caused by pivoting of the arm/gate assembly about the hinge.
A correlation for the volume of material removed as a function of the flow velocity
is [15]:
V
=
(3.1)
(KF) 3FAe
11
where
V
= rate of volume removal
K, F
P
= material constants
= material hardness
Fn
= normal force =
W
= weight of gate
Wa
= weight of arm
sin( ave
[W -
Wa/2l sin( 0ave)
- W a/2)bg[(W
_ K pA(vave
)2g
b
= buoyancy factor for metal in liquid
g
=
=
=
=
p
A
vave
At
6max
'min
v.
vm
weddy
rp
acceleration of gravity
liquid density
gate area
average flow velocity
= sliding distance = 2(Oax =
=
=
=
min)eddy
maximum angle of displacement (calculate using vmax)
maximum angle of displacement (calculate using vmin)
maximum flow velocity
minimum flow velocity
eddy frequency = 0.04 vave
r
=
p
= pipe radius
Note that vmax and vmin characterize the short time scale fluctuations of flow
velocity about vave'
For a given valve in a given application, the only random variable in
Equation (3.1) is vave, the average flow velocity. Thus, if the distribution for vave
can be developed, the distribution for the amount of hinge wear can be developed
very simply from Equation (3.1).
Valve tapping, the striking of the valve stop by the gate, becomes a problem
when the flow is not strong enough to keep the gate in the fully open position
(pegged against the stop) and is not weak enough to allow the gate to swing freely.
Figure 6 presents an experimentally derived map of the three different regimes
(pegged, tapping, and swinging free) as a function of flow velocity and the L/D
12
ratio, where L is the distance of the valve from the nearest flow disturbance in the
pipe and D is the pipe diameter. The L/D ratio is an indication of the amount of
turbulence at the valve location; high values are associated with fully developed
flow, which is less likely to lead to tapping. Not shown in Figure 6 is the frequency
of tapping, which probably increases with decreasing L/D.
If the frequency of tapping can be determined as a function of vave and L/D,
figures such as Figure 6 [16] can be used to determine the distribution of the number
of taps in a given time interval (recall that vave is a random variable). Mechanical
models needed to translate the tapping into the likelihood of cotter pin failure, nut
backing off, and subsequent displacement of the gate are still needed.
Check Valve Failure Data
The above models for check valve behavior focus on specific valve failure
modes which can be analyzed using physical principles. While these modes have
actually been observed, they are not all-inclusive. Failure mechanisms less
amenable to rigorous theoretical analysis, such as the plugging of the valve by trash
in the system, may be equally important, if not more so.
To determine the importance of these other failure modes, and to obtain a
3.2
general picture of the variety of failures that may be experienced by a mechanical
component in real service, descriptions of 63 check valve failures were obtained from
Nuclear Power Experience (NPE) [17], covering the years 1975 through 1983. NPE
is a private compilation of event narratives based largely, but not entirely, on the
Licensee Event Reports (LERs) submitted by the utilities to the United States
Nuclear Regulatory Commission. The narratives vary greatly in detail, but usually
indicate such information as the plant name, the date of the incident, the system
involved, the failure cause, the failure mode, and the consequences of the event.
A breakdown of the fail-to-open failure data (12 events) for swing check
valves is presented in Figure 7; a similar breakdown for the fail-to-close failure
mode (40 events) is presented in Figure 8. Table 1 provides a listing of all of the
events considered. The two figures show that both random (e.g., jamming by a
foreign object) and degradation-related failures are important. Thus, a complete
failure model must address both types of failure.
13
Table 1 - Check Valve Failure Data (Page 1 of 2)
Record
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Event
BWR-2.VII.E.p6.34
BWR-2.VII.A.p7.40
BRW-2.VII.C.p14.61
BWR-2.VII.D.p4.16
BWR-2.VII.C.p14.61
BWR-2.VII.E.p3.11
BWR-2.VI.E.p17.65
BWR-2.VII.A.p13.76
BWR-2.VII.A.p14.83
BWR-2.VII.A.p16.94
BWR-2.VII.A.p16.95
BWR-2.VII.D.p36.171
BWR-2.VII.D.p40.185
BWR-2.VII.D.p48.236
BWR-2.VII.E.p22.90
BWR-2.VII.E.p33.139
BWR-2.VII.E.p47.213
BWR-2.VII.F.p18.65
BWR-2.VIII.C.p21.86
BWR-2.VII.D.p40.185
BWR-2.VII.D.p48.236
BWR-2.VII.E.p22.90
BWR-2.VII.E.p33.139
BWR-2.VII.E.p47.213
BWR-2.VII.F.p18.65
BWR-2.VIII.C.p21.86
BWR-2.IV.B.p68.213
BWR-2.VII.D.p59.291
BWR-2.VII.E.p51.235
BWR-2.VII.F.p52.215
BWR-2.VIII.C.p51.24
BWR-2.VIII.C.p58.28
BWR-2.VIII.C.p59.28
Plant
Brunswick 2
Brunswick 2
Dresden 2
Quad Cities 2
Dresden 3
Pilgrim
Cooper
Browns Ferry 2
Hatch 2
Brunswick 1
Hatch 1
FitzPatrick
FitzPatrick
Vermont Yankee
Browns Ferry 3
Browns Ferry
Browns Ferry 2
FitzPatrick
Vermont Yankee
FitzPatrick
Vermont Yankee
Browns Ferry
Browns Ferry 2
Browns Ferry 2
FitzPatrick
Vermont Yankee
LaSalle 1
Brunswick 1
Monticello
Lasalle 1 & 2
Hatch 1
FitzPatrick
Hatch 2
Failure
Mode
Component
Type
fto
fto
ftc
ftc
ftc
fte
ftc
ftc
fto
ftc
fto
ftc
ftc
swing check
swing check
stop-check
na
stop-check
rising plug
na
swing check
swing check
swing check
stop-check
swing check
swing check
swing check
na
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
ftc
fto
ftc
ftc
ftc
ftc
ftc
ftc
fto
ftc
ftc
ftc
ftc
ftc
ftc
ftc
ftc
ftc
ftc
ftc
Failure
Type
jammed closed
disassembly
improper seating
foreign object
improper seating
foreign object
foreign object
disassembly
disassembly
foreign object
vibrated closed
foreign object
disassembly
improper seating
na
jammed open
foreign object
foreign object
improper seating
disassembly
improper seating
jammed closed
jammed open
foreign object
foreign object
improper seating
jammed open
improper seating
disassembly
foreign object
improper seating
jammed open
jammed open
Failure
Cause
na
na
na
na
na
loose object
loose object
pin
stud
loose object
na
loose object
pin
na
na
na
crud buildup
loose object
stud-gate
pin
na
na
mechanical
crud buildup
loose object
stud-gate
chemical
na
pin
loose object
stud-gate
mechanical
na
Table 1 - Check Valve Failure Data (Page 2 of 2)
Record
H
U1
Event
Plant
Failure
Mode
Component
Type
Failure
Tve
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
BWR-2.VIII.C.p69.33
BWR-2.VIII.C.p70.33
BWR-2.VIII.C.p72.33
BWR-2.XI.A.pl01.430
BWR-2.XI.A.pl01.430
PWR-2.VII.A.p52.172
PWR-2.VII.A.p53.175
PWR-2.VII.A.p104.39
PWR-2.VII.A.p101.39
PWR-2.VIII.B.p13.43
PWR-2.VIII.B.p30.11
PWR-2.VII.B.p32.127
PWR-2.VIII.B.p37.15
PWR-2.VIII.B.p42.18
PWR-2.VIII.B.p43.18
PWR-2.VI.E.p57.199
PWR-2.VI.E.pl 17.378
PWR-2.VI.E.p122.386
PWR-2.VII.A.p73.275
PWR-2.VIII.B.p51.22
PWR-2.VIII.B.p52.23
PWR-2.VIII.B.p72.31
PWR-2.VIII.B.p97.42
PWR-2.VIII.B.p106.4
PWR-2.VIII.B.p114.4
PWR-2.VIII.B.p131.5
PWR-2.VI.E.p171.555
PWR-2.VI.E.p171.555
PWR-2.VII.E.p38.168
Monticello
ftc
Hatch 2
ftc
Peach Bottom 2
ftc
Dresden 2
ftc
Dresden 3
ftc
Indianan Pt. 2
ftc
San Onofre 1
ftc
Arkansas One 2
ftc
Arkansas One 2
ftc
Robinson 2
ftc
Palisades
fto
Calvert Cliffs 1
fto
fto
Palisades
Davis Besse 1
ftc
Palisades
fto
Beaver Valley 1
ftc
Surry 1
ftc
North Anna 1 & 2 na
Beaver Valley 1
ftc
Cook 2
ftc
Calvert Cliffs 1I fto
fto
Palisades
fte
Surry 2
Surry 2
fte
Davis-Besse
ftc
fto
Summer
Byron 1
fto
Byron 1
fto
Maine Yankee
ftc
swing check
swing check
swing check
swing check
swing check
swing check
tilting check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
swing check
na
swing check
swing check
swing check
swing check
swing check
na
swing check
swing check
swing check
improper seating
jammed open
jammed open
disassembly
disassembly
disassembly
improper installation
jammed open
jammed open
foreign object
jammed closed
improper installation
jammed closed
jammed open
jammed closed
foreign object
disassembly
na
improper seating
improper seating
foreign object
jammed closed
improper seating
jammed open
jammed open
jammed closed
improper installation
improper installation
foreign object
63
PWR-2.VIII.B.p134.574
Surry 1 & 2
ftc
swing check
foreign object
Failure
Cause
stud
chemical
mechanical
stud
shaft
pin
na
mechanical
mechanical
loose object
na
na
chemical
chemical
chemical
loose object
pin
na
na
na
loose object
chemical
stud-gate
na
chemical
na
na
na
corrosion
product
loose object
Flow Regions
20.0
-"Swinging
18.0
16.0
A
14.0
Free
A
Tapping
0
Pegged
A
-Pegged/Tapping
V
e
12.0
0
10.0
C
t
y
A
Tapping/Swinging
0
A
A
00
A
8.0
6.0
-
4.0
-
-I
2.0
-
0.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
L/D's from upstream disturbances
Fig. 6:
REGIONS OF FLOW-INDUCED MOTION IN CHECK VALVES [16]
7.0
8.0
Foreign
object
Disassembly
Jammed
closed
Improperly
installed
Fig. 7: DISTRIBUTION OF FAILURE TYPES,
SWING CHECK VALVE FAIL-TO-OPEN (FTO)
17
Foreign
object
Disassembly
Improperly
installed
Improper
seating
Jammed
open
Fig. 8: FAILURE TYPE DISTRIBUTION, SWING CHECK VALVE
FAIL-TO-CLOSE (FTC)
18
4. Check Valve Analysis
Failure Mode Identification
A fault tree for check valve failure (FTC) is shown in Figure 9. This tree is
developed based on the discussion in Reference 15, the NPE failure data [17], and
interviews of Professor P. Griffith and engineering personnel familiar with naval
nuclear propulsion systems. The CAND gate, as discussed in Section 2, is a
convenient shorthand for situations where infinite combinations of
4.1
continuous-valued variables can lead to the top event.
The minimal cut sets (MCS) for the FTC failure mode are given in Table 2.
As expected, most of these cut sets are of first order, there being little redundancy
within the valve. This is likely to also be the case for most nuclear plant
components.
The quantification of each branch/event in the fault tree of Figure 9 follows
along one of two paths. The first path, involving a more or less conventional
statistical analysis, is used for events under AND and OR gates. These events,
described as being "random" in Section 3, lead to discrete changes to the system,
and are well treated by current analyses. For example, the frequency at which loose
objects hold the valve open can be estimated on the basis of the number of events
observed and the length of the period of observation [3].
The second path is used when dealing with events following CAND gates
(whose cut set members are denoted by asterisks in Table 2). These events, while
having some random characteristics, are largely the outcome of physical processes
which can be modeled. An example of such modeling is described in Section 3 and is
quantified in Section 4.3.
Statistical Analysis of MCS Frequencies
If data are available, the parameters of the failure model can be estimated in
the same manner as used in current risk studies. Since the amount of available data
is usually small, a Bayesian approach is best suited for the analysis [3].
Let A be the parameter to be estimated based on evidence E; Bayes' Theorem
4.2
states that
19
rl(A IE)
=
Y
(EjA) ir0(A)
L(EIA) r 0 (A) dA
(4.1)
where r, (AIE) is the posterior probability density function (pdf) for A, L(E IA) is
the likelihood function, and 7r0 (A) is the prior pdf for A. The denominator is simply
a normalization factor to ensure that the posterior pdf integrates to unity over all
possible values of A.
The prior distribution, w0(A), quantifies the analyst's state of knowledge
concerning the value of A prior to observing evidence E. The prior distribution is
commonly used to incorporate "engineering judgment" into the analysis, and plays
an important role when the available data are limited. The likelihood function,
L(E IA), gives the conditional probability of observing E, given that A takes on a
certain value. This function can be used to incorporate non-statistical as well as
statistical evidence. For example, Reference 3 describes methods to treat expert
opinions in a Bayesian analysis.
To illustrate the approach, the available data are used to quantify the
frequency of valve disassembly, Ad. This is the parameter which governs
probability of observing any number of disassemblies in a given time period:
P{r disassemblies in time T} =
(AdT)r eAd
r!
(4.2)
where the conventional assumption that the number of disassemblies is Poisson
distributed is used. If the observed evidence consists of the pair of values (r,T), it
can be seen from the definition of the likelihood function that the right hand side of
Eq. (4.2) is actually the likelihood function for this particular problem.
For convenience, we assume that the prior distribution can be represented by
a "noninformative" form [3,18]:
(4.3)
rO(Ad)
d
Note that this distribution is improper, since it is unbounded at Ad = 0. The
noninformative form is used as a mathematical convenience to represent the
behavior of 7ro(Ad) over the range of interest; if no data are available, a prior
20
distribution which treats the analyst's state of knowledge more carefully should be
developed, since it will directly influence the results of the analysis.
Using the noninformative prior distribution, it can be shown that Eq. (4.1)
results in
T(AdT)r-le
(r-1)!
1(Adr,T) =
dT
The mean and variance of Ad are, respectively,
E[Ad
(4.5)
Var[A d]
r
T
For the case of the fail to close swing check valve failure mode, Table 1 shows
that the data set includes 8 valve disassemblies. Thus, r = 8. However, an
appropriate value of T is more difficult to determine. T represents the total
experience (in valve-years) for swing check valves accumulated over the period 1975
through 1983. To estimate T, we need to know the number of swing check valves in
each plant which are similar to the valve being analyzed, and the amount of
relevant experience (plant years) for each plant.
It should be noted that T is an inherently uncertain quantity. Uncertainty
arises when deciding which valves are similar to the valve of interest, and when
determining the appropriate amount of plant experience (i.e., deciding among
operating years, calendar years, or some other measure). To illustrate the approach,
we assume that T is lognormally distributed with a mean value of 71,150
valve-years (obtained by multiplying the number of swing check valves in the
safety-related systems of the Seabrook Unit 2 PWR [19] by the total number of
U.S. plant years of operation for the period 1975 through 1983) and a logarithmic
standard deviation (aT) of 1.0 (corresponding to a range factor of 5.2).
The final distribution for Ad, given r and a distribution for T, is obtained by
recognizing that 7r1 (Ad Ir,T) is a conditional distribution for Ad, given r and T.
Thus,
21
00
,(A dIr,p(T))
=
{r
d(AdIr,T)p(T)dT
(4.6)
0
where p(T) is the lognormal distribution for T described above and where
l(A dIr,T) is given by Eq. (4.4).
Eq. (4.6) can be evaluated using standard quadrature techniques. The
resulting moments of Ad are given in Table 3 and the distribution of Ad is
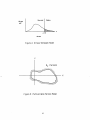
characterized in Figures 10 and 11. Also shown is the distribution obtained when
UT = 0.001 (i.e., T is essentially a certain quantity). It can be seen that the
decrease in aT leads to a small (factor of 1.5) decrease in the mean value of Ad, but
a large (factor of 15) decrease in the the variance. Thus, the uncertainty in Ad can
be badly underestimated if uncertainties in the data are not properly accounted for.
Continuous Variable MCS Quantification
To treat minimal cut sets involving continuous variables (events under a
CAND gate), a somewhat different approach is required. For example, consider
minimal cut set number 1, involving improper seating of the gate. In this case,
combinations of wear conditions in the shaft, stud and gate can lead to increased
free play and eventual improper seating. The following discussion illustrates the
4.3
modeling process, using the valve wear model described in Section 3.
Two cases can be considered at this point. First, we notice that any single
part in consideration (i.e., the shaft, the stud or the gate) can lead to improper
seating independently. For example, wearing in the shaft alone can be responsible
for the gate displacement even if the stud and gate have undergone little or no
wearing at all. If we limit ourself, initially, to the consideration of this case only
(independent failures), then the CAND gate degenerates into an OR gate and we are
left with the study of the probabilities of extreme displacement due to each
component separately.
4.3.1 Independent Failures
Let us examine the case of displacement due to shaft wear. The other two
cases will involve a similar procedure. The analysis requires the following steps:
a)
Identification of the random state variables which define the shaft
deterioration process.
22
b)
Estimation of the probability distributions of the random variables
identified in (a).
c)
Modelling of the deterioration process.
d)
Definition of a failure region (domain in which the values of the state
variables correspond to excessive wear).
e)
Computing the probability integral over the failure region (exactly or
with an approximation such as the one described in the appendix).
In the case of shaft wear, steps (a) and (c) have been already carried out in
Section 3 of this report. Eq. (3.1) describes the wearing process in terms of the rate
of shaft material volume removal. In that equation, the average velocity of the fluid
is the only random state variable (as long as the maximum and minimum
fluctuation velocities, vmax and vmin, are functions of vave). Then
V
Vshaft (ave)
-
K 1K 2K3
v e
si-1
K2
max
n-1
K2.7
where
1
=
37(W - Wa/ 2 )
(W - Wa/ 2 )bg
IC2
K=
3
KpA
0.04
r
p
Step (b), estimation of the distribution of vave, is straightforward in principle,
although the necessary data may not be available. Note that vave is a function of
time; what is needed, therefore, is an estimate of time (perhaps expressed in terms
of fractions of the operating year) the component is subjected to a characteristic
flow rate. Such an estimate might be obtained, for example, by assessing the
fraction of time the plant spends in full load, partial load, and no load conditions,
and determining the average flow rates for each of these conditions. Uncertainties
in the assessment are expressed as probability distributions for the model
parameters (e.g., the fraction of time spent in each condition).
23
The failure region (step (d)) for this case can be formally defined to be that
for which
Vshaft(ave) > Vshaft(vave)
(4.8)
where V is the integral over time of Eq. (4.7) and V is a critical value for shaft
wear (recall that we are assuming little or no wear for the stud and the gate in this
case). This criteria can be recast into the following standard form:
Fshaft(vave) > 0
(4.9)
where
Fshaft(ave) = Vshaft(vave) - Vshaft(vave)
(4.10)
Of course, the problem is to determine V . This parameter is a direct
function of the valve design, which establishes nominal clearances, and the assembly
tolerances. Therefore, these equations provide the connection between the
measurable, physical characteristics of the valve and the valve reliability (with
respect to the particular failure mode being analyzed). As a result, they indicate
how changes in design and manufacturing can lead to reliability enhancement or
degradation.
It is important to note that assembly tolerance is a random variable, which
means that the critical shaft wear, V is also random. This uncertainty is
accounted for using standard stress-strain modeling techniques [9].
The remaining step in the analysis is that of computing the probability
integral
(4.11)
Pshaft = P[Fshaft(ave) > 0]
Since the previous steps have determined the failure region and the distribution of
vave, this is a problem in numerical analysis. The software package (FORM) used
to perform this analysis is documented in Reference 7; this package employs the
First Order Reliability Method described in the Appendix. It is also suitable for
handling many more variables and complex failure regions.
24
Following the same approach, similar relations such as Eq. (4.11) can be
developed for stud and gate wear. In these latter cases, wear models analogous to
Eq. (4.7) must be developed for both parts. Assuming that such relations can be
found, the probability of improper seating assuming independence of failure modes is
then
is
shaft +Pstud +Pgate
(4.12)
(using the rare event approximation).
4.3.2 Dependent Failures
While the three different failure mechanisms do not lead independently to
overall component failure, the procedure used in the previous discussion is also
applicable to the more realistic situation of dependent mechanisms. In this latter
case, a failure condition defined in terms of the three wear variables must be
defined, and a joint probability distribution for the variables assessed:
is = P{Fis(Vshaft,Vstud,Vgate) > 0}
(4.13)
Notice that Fis degenerates into Fshaft when Vstud = Vgate = 0, and similarly for
F stud and Fgate'
This example for treating continuous variables has been aimed at the
"Improper Seating" failure mode. Examination of the "Mechanical Jamming"
failure mode (MCS 5) shows that shaft, stud, and gate wear also apply, although the
failure function Fmj may be very different. Note also that the interference term
between the two MCSs (which are essentially connected by an OR gate) may not be
negligible.
4.3.3 Quantification
As an example of the actual computation of the failure probability associated
to a CAND-gate, we analyze the improper seating failure mode for the swing check
valve. The purpose of this analysis is to illustrate in detail the computational
procedure. Thus, arbitrary values are used for the limited number of parameters for
which no data are currently available.
25
It is assumed that the gate seats improperly when its vertical displacement
due to wear at the hinge and at the stud-gate connection, exceeds the actual
tolerance which results from the design tolerance and potential construction errors.
It is assumed that the valve is maintained and brought back to initial conditions
every year. The probability of failure (for improper seating) is then defined as the
probability that the valve seats improperly in any given year of operation between
two consecutive inspections.
Hinge Wear. The wear at the hinge is assumed to be governed by the model
described by Eq. (4.7). Typical values for the material and geometrical parameters
of a 10 inch diameter valve are given in Table 4. For this analysis, it is assumed
that the average flow velocity, vave, takes on the nominal value during reactor
operation, and is zero when the reactor is not operating. During operation,
therefore, the nominal rate of material removal is V = 0.27 inch 3 /year.
The area of the cross-section of the hinge pin which is removed can be
computed by dividing the total volume of material removed from the hinge (V -to)
by the length of the pin (2- rP), where to is the time of actual operation during the
year of observation. Assuming that the vertical drop dh is proportional to the
square root of the area removed from the circular cross-section:
dh
Vt
dh =P 2 P
(4.14)
where for the sake of illustration the constant p1 is assumed to have a value of 3.4.
The uncertainty associated to the expression for V is described by assuming a
normal distribution with mean equal to the nominal value just found (0.27 in 3 /yr),
and standard deviation representing a nominal variability of ±10%about the mean
V ~ N(p = 0.27, o-= 0.03) inch 3/year
Stud-Gate Wear. The assumed mechanism of wear at the connection of the
arm and the gate is assumed to be initiated by the failure of the cotter pin that
holds the nut to the stud. When this happens the nut slowly backs off causing
26
increasing free play between the stud and gate, leading to increasing wear of the two
parts. Let t be the operating time when the cotter pin fails. If t > to, no drop
due to this wear mechanism is assumed to take place. If t < to, the drop due to
arm-stud wear, da, is assumed to be a quadratic function of the time of operation
after the cotter pin breakage:
da
*2
P 2 (to -t )
if
0
otherwi s e
*
t
<to
(4.15)
For purposes of illustration, let p2 = 3.3 .
The time of cotter pin failure, and the time of actual operation are random
variables which we assume to be normally distributed with means and standard
deviations as follows:
t
to
N(jp = 0.90, a = 0.03) years
N(p = 0.85, a = 0.03) years
The mean of to is obtained from data on nuclear power plants down time; the mean
time to cotter pin failure is assumed for the purpose of illustration.
*
Tolerance. The actual tolerance, or permissible vertical drop of the gate, d
is given by the sum of a design tolerance p3 , and a construction error c:
*
d =p
3
+
(4.16)
where a typical value for p3 is 0.787 inch and Eis assumed to be normally
distributed:
S~ N(pL = 0.0, a = 0.0472) inch
State Equation. From the previous assumptions it is possible to assemble the
following state equation:
27
g(x) = p3 + x4 - pl(x3x1/10)1/2 ~p2 (x1
)2
(417)
and the corresponding failure condition:
(4.18)
g(x) < 0
The state variables (x) are:
x1 =to
*
x2 =t
x3
V
xx4- =(
Results. Once the state equation is developed, the failure probability can be
determined as
Pf = P{g(x) < 0}
(4.19)
In this analysis, the First Order Reliability Method (FORM), described in the
Appendix, is applied. The computer code used which employs this method (also
called FORM) is described in Reference 7. Alternative approaches for solution
include using exact distributions, moment methods, or Monte-Carlo methods.
The result obtained using FORM is that Pf = 6.6 x 10 . This is the
probability (for a year of operation) that the check valve will fail to close due to
improper seating of the gate. Again, although this number is lower than the valve
disassembly result obtained earlier, it should not be viewed as a serious estimate,
since arbitrary values were assigned to the parameters p1 and p2 , and since the
failure model for arm/gate wear, while plausible, is not based on any rigorous
derivation. The calculation does indicate what types of input are needed to
estimate the component reliability. It also shows that once the failure model (state
equation) is developed, the failure probability computation can be accomplished
quite easily using FORM.
Because the FORM code is quick running, sensitivity studies can be performed
quite easily. As a simple example, Table 5 shows the results obtained from
28
modifying each of the model constants, pi, and the distribution constants (p,-)
individually. Variations are set at ± 10% of the nominal (base case) value.
The analysis identifies two parameters of importance: the mean of x 2 and p .
3
In both of these cases, the computed value of Pf is comparable to the valve
disassembly failure rate. Thus, while the base case value of Pf indicates that
improper seating is not a significant contributor to the total failure probability of
the valve, the sensitivity study results show that small variations in parameters can
change this result. This shows the importance of the treatment of uncertainties; a
realistic analysis should spend significant resources in characterizing the
uncertainties in models and model parameters, as well as on obtaining reasonable
nominal estimates for the model parameters.
Validation of First Order Analysis Results. FORM is a very efficient
technique to obtain approximate solutions, but it is important to assess the
accuracy of its results. Some work has been done in this respect, and according to
Reference 7 the probability estimate can be insufficiently accurate in
high-dimensional problems (for example with more than thirty random variables).
In this case, it is suggested that the solution be checked using the Second Order
Reliability Method (see Reference 20). Other numerical problems can occur when
one variable dominates the failure (or survival) probability and this probability is
very small (or very large). However, it is reasonable to assume that the calculated
results are accurate to the first order in the range of 104 < Pf 5 1 - 10.
For the improper seating problem treated in this analysis, the solution of
FORM has been check by repeating the last sensitivity listed in Table 5 using a
standard Monte Carlo simulation. The result of this test is that the FORM value is
within 4% of the Monte Carlo result, and is therefore quite acceptable for our
purposes.
29
Table 2 - Minimal Cut Sets for Swing Check Valve (Fail to Close)
(*) 1.
2.
Loose Object Obstruction
3.
Buildup Obstruction
4.
Backward Installation
(*) 5.
*
CAND( Worn Shaft - Worn Stud - Worn Gate) leading to improper
seating
CAND( Worn Shaft - Worn Stud - Worn Gate) leading to mechanical
jamming
6.
Shaft Corrosion
7.
Hole in Valve (corrosion)
8.
Shaft Broken
9.
Arm Broken
10.
Stud Broken
11.
Gate Broken
Probability of MCS must be evaluated using continuous variable methods
30
Table 3 - Characteristic Parameters for r1 (Ad IE)
Parameter
E[Ad]
Var[Ad]
aT = 1.0
aT = 0.001
1.6 x 104/yr
1.1 x 104/yr
2.8 x 10
1.9 x 10-9/yr 2
31
/yr2
Table 4 - Typical Values for Check Valve Wear Model Parameters
Parameter
KI
P
F
W
Wa
b
Value
5 X 10-3 (dimensionless)
18.000 psi
7.47 lb
13 lb
6.5 lb
g
p
A
.88 (dimensionless)
384 inch/sec 2
0.036 lb/inch 2
78 inch 2
Vave
K
sin 0ave
7.4 inch/sec
28 (dimensionless)
0.766
'eddy
0 .
0.0592 sec-1
200
min
0max
Al
800
0.124 inch/sec
32
Table 5 - Sensitivity Analysis Results
Parameter
m
Nominal
Value
Variation
Failure
Probability
.85
+10%
.99-5
-10%
.35-4
+10%
.58-6
-10%
.77-6
+10%
.20-5
-10%
.17-3
+10%
.56-6
-10%
.84-6
+10%
.47-5
-10%
.88-7
+10%
.42-6
-10%
.21-5
+10%
.27-5
-10%
.11-6
+10%
-10%
.58-4
+10%
-10%
.77-6
+10%
-10%
.50-9
.26-3
x1
ax
mx
2
x2
mx
3
x3
x4
p1
.03
.90
.03
.27
.03
.0472
3.4
3.3
p3
.787
33
.37-8
.52-6
La)
4:-
Fig.
9:
FAULT TREE FOR SWING CHECK VALVE FAIL-TO-CLOSE
5. Concluding Remarks
This report investigates the modeling of component reliability, a necessary
step when reliability goals are specified for a system design. Using swing check
valves as an example, it is shown that a wide variety of failure modes are possible,
some of which involve continuous component degradation and are not amenable to
standard statistically-based reliability analysis. Physical models for component
behavior are required to handle these latter failure modes.
The report shows how the two types of failure analyses can be integrated into
a reliability analysis and presents a limited quantification of some of the factors in
the check valve failure model. An analysis is performed for a discrete failure mode
(valve disassembly) for which the failure data are uncertain. A Bayesian approach
is used to estimate the frequency of this mode. The likelihood that the valve seats
improperly due to continual wear of component parts is treated by developing a
model for part wearing and displacement and quantifying this model using First
Order Reliability Method (FORM) analysis.
While values for a limited number of the model parameters are selected
arbitrarily, the analysis is useful in that not only does it demonstrate the procedure
and tools needed to obtain results, it also shows how the importance of different
model parameters (e.g., the value of the design tolerance) can be determined. This
importance is measured in terms of nominal contribution to unreliability, and in
terms of the sensitivity of the component reliability to uncertainties in the
parameter values. Thus, the analysis procedure can be used to determine if a part
in a component should be improved, if additional data characterizing the part
should be gathered, or both.
While the methodology has been applied to a swing check valve for
demonstration purposes, it is clearly not limited to such simple cases, nor even to
existing components. Consider, for example, the shutdown rod assemblies for the
secondary self-actuated shutdown system described in Reference 21. Based on the
proposed assembly design and operating/maintenance procedures, a fault tree can be
constructed to identify postential failure modes. This fault tree can incorporate
continuous as well as discrete variables. Quantification of the fault tree gates can
be accomplished by conventional methods, in the case of discrete variables, and by
such methods as FORM, in the case of continuous variables. Note that if failure
data are completely lacking, as may be the case for innovative components,
35
simulation models may be needed to quantify the discrete event failure modes.
As in the case of the swing check valve example, the analysis would:
-
provide a basis for rigorous reliability estimates in the case of strongly
interdependent variables even in absence of failure data, and
-
determine relative importance of the model parameters and therefore
indicate which ones need to be investigated with additional experimental
and/or analytical methods.
Of course, to perform the analysis, models for the degradation failure modes
are needed, as well as documentation concerning system design, operation, testing,
and maintenance. For many components, a significant effort may be required to
develop these models. An additional potential problem is that there may be
interactions between the failure processes characterized by discrete events and those
characterized by gradual degradation; methods to treat this situation have not been
developed in this report, and require additional investigation.
36
6. References
1)
U.S. Nuclear Regulatory Commission, "Reactor Safety Study: An Assessment
of Accidental Risks in U.S. Commercial Nuclear Power Plants," WASH-1400,
NUREG-75/014, October 1975.
2)
American Nuclear Society and IEEE, "PRA Procedures Guide - A Guide to
the Performance of Probabilistic Risk Assessments for Nuclear Power Plants,"
U.S. Nuclear Regulatory Commission, NUREG/CR-2300, April, 1983.
3)
G. Apostolakis, "Bayesian Methods in Risk Assessment," Advances in Nuclear
Science and Technology, 13, 415-65 (1981).
4)
K.N. Fleming, "A Reliability Model for Common Mode Failure in Redundant
Safety Systems," Proceedings of the Sixth Annual Conference on Modeling
and Simulation, Pittsburgh, April 1975.
5)
J.A. Hartung, H.W. Ho, P.D. Rutherford, and E.U. Vaughan, "The Statistical
Correlation Model For Common Cause Failure," Proceedings of the Annual
Conference of the Society for Risk Analysis, August 1-3, 1983.
6)
A. Mosleh and N. Siu, "A Multi-Parameter, Event-Based Common-Cause
Failure Model," Paper M7/3, Proceedings of the Ninth International
Conference on Structural Mechanics in Reactor Technology, Lausanne,
Switzerland, August 1987.
7)
S. Gollwitzer, F. Guers, and R. Rackwitz, FORM (First Order Reliability
Method) Manual. Nymphenburger Str. 134, 8000 Munchen 19, West
Germany, 1987.
8)
U.S. Nuclear Regulatory Commission, "Loss of Power and Water Hammer
Event at San Onofre, Unit 1, on November 21, 1985," NUREG-1190, January
1986.
9)
M.L. Shooman, Probabilistic Reliability: An Engineering Approach,
McGraw-Hill, New York, 1968.
10)
M. Hohenbichler, et al., "New Light on First- and Second-Order Reliability
Methods," Structural Safety, 1, (1987).
11)
G.I. Schueller, "A Critical Appraisal of Methods to Determine Failure
Probabilities," Structural Safety, 1, (1987).
12)
M. Hohenbichler and R. Rackwitz, "First-Order Concept in System
Reliability," Structural Safety, 1, (1983).
13)
M. Shinozuka, "Basic Analysis of Structural Safety," Journal of the Structural
Division of ASCE, 109, (1983).
14)
M.J. Grimmelt, et al., "Benchmark Study of Methods to Determine Collapse
Failure Probabilities of Redundant Structures, Structural Safety, 1, (1983).
37
15)
P. Griffith, "Check Valve Inspection and Redesign," Proposal to Northeast
Utilities, 1987.
16)
J. Snopkowski and P. Griffith, Letter to C. Nalezney, EG&G Idaho, NRC
Public Document Room, April 1, 1986.
17)
S.M. Stoller, Nuclear Power Experience, updated monthly.
18)
R.L. Winkler and W.L. Hays, Statistics, 2nd d., Holt, Rinehart, and
Winston, 1975.
19)
Pickard, Lowe and Garrick, Inc., "Seabrook Station Probabilistic Safety
Assessment," prepared for the Public Service Company of New Hampshire and
the Yankee Atomic Electric Company, PLG-0300, December 1983.
20)
S. Gollwitzer, F. Guers, and R. Rackwitz, SORM (Second Order Reliability
Method) Manual. Nymphenburger Str. 134, 8000 Munchen 19, West
Germany, 1987.
21)
Rockwell International, "Sodium Advanced Fast Reactor Preliminary Safety
Information Document," AI-DOE-13527, Revision 7, prepared for the U.S.
Department of Energy, September 1986.
38
Appendix - An Overview of First Order Reliability Analysis
In this appendix, the first order reliability analysis method is briefly
described. Additional details are provided in Reference 7 and References 10-14.
Problem Formulation
The state of the system is described by a set of known and uncertain
parameters. All the uncertain quantities are listed in a time-invariant
n-dimensional random vector x.
A limit state is defined (e.g. excessive deformation, excessive stress, cracking,
etc.) such that if the system is in that state, than the system is considered to have
failed; otherwise the system is said to survive.
X2
RF
:. :::.... (failure)
S
(survival)
We are interested in the probability Pf that the system fails.
If the joint cumulative distribution function (CDF) P . is known, than the
problem of computing Pf is called a full distribution (FD) reliability problem.
If only the mean and standard deviation of x are available then Pf is not
uniquely defined and one has to be satisfied with other measures of the system
reliability, the so called reliability indices. This last problem is referred to as second
moment (SM) reliability analysis.
The limit state allows the partition of the space of x into two parts: a safe
region, R5 , which is the collection of all points for which the system survives, and a
failure region RF which is the complement of R5 .
The probability of failure is given by:
A-1
Pf
= P{x belongs to RF1
= 1 - P{ belongs to Rs}
= 1-
dP (x)
S
In cases where x has a high dimension, the computation of this integral is
usually impractical. Approximate procedures have been developed for such cases.
First Order Analysis
Two factors play an important role on the computation of Pf: the type of
failure condition and the type of CDF. First order analysis takes advantage of the
fact that if the x has a multivariate normal distribution, and if the failure condition
is linear, then Pf can be easily obtained.
A linear failure condition is one for which survival depends on x only through
a linear function
y= a+
TX
(A.1)
where the condition is of the type
*
y > y
For example, let x1 be a random normal load, x2 a random normal resistance
and x 1 > x 2 the failure condition. We can define y as y = (x1 - x2). Then, if mi is
the mean value of xi, o1 its standard deviation, and p is the correlation coefficient
between x1 and x2'
y
N(myo ) (y is normally distributed)
y~=
y=O
where
m
=
M1 -m2
2
2
1'
A-2
X
2
9xl
The probability of failure is given by
12
1
Pf
-
e
=
dz
where
m
m2
-
y
The parameter
# can
be seen as the minimum of the standardized distance of the
mean of x from the boundary.
If x is normal but the failure condition is not linear of the type
*
y = g(x) > y
one can still use, as an approximation, the procedure shown in the previous example
after having linearized the boundary B with a plane tangent to B at a point x
This is the basis of the first order method.
Best results are obtained by selecting the linearization point as the one for
which the likelihood of failure is maximized. The determination of this point, called
the #-point, varies according to the type of joint CDF. If x is standard normal, then
the #-point is the point on the boundary for which the Euclidean distance from the
mean of x is minimized.
A-3
p-point
::
If x is normal but not standardized, one has to minimise the so called
Mahalanobis distance which is defined as
1
[~~)=(x
- rn)T
where
-1
-n)2
is the covariance matrix for x.
If x is not normal, it can be transformed to normality with a standard
procedure such as the Rosenblatt transformation. If the failure condition in the
normal space happens to be linear then we can directly use the procedure of the
previous example; otherwise we can linearize it at the /3-point, as explained above,
and then proceed as in the example.
The process of transforming x to the normal space can be computationally
very demanding. A more efficient strategy has been developed in which x is not
transformed to normality, but rather approximated to a normal distribution. This
procedure of "normal tail approximation", is known as the Rackwitz-Fiessler
algorithm; it can greatly increase the efficiency of first order reliability analysis.
A-4