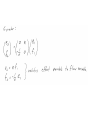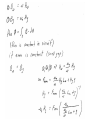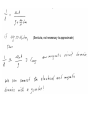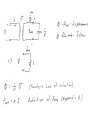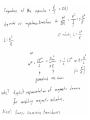* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lumped Modeling with Circuit Elements, Ch. 5, Text
Surge protector wikipedia , lookup
Index of electronics articles wikipedia , lookup
Nanogenerator wikipedia , lookup
Lumped element model wikipedia , lookup
Electronic engineering wikipedia , lookup
Electrical engineering wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Mechanical filter wikipedia , lookup
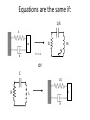
Lumped Modeling with Circuit Elements, Ch. 5, Text • Ideal elements represent real physical systems. – Resistor, spring, capacitor, mass, dashpot, inductor… – To model a dynamic system, we must figure out how to put the elements from different domains together. – Alternatives include numerical modeling of the whole system. Lumped element modeling offers more physical insight and may be necessary for timely solutions. Example. Electrical: Resistor-InductorCapacitor (RLC) system. C R i L No power source, transient response depends on initial conditions B1, B2 depend on initial conditions Example. Mechanical: Spring-MassDashpot system. x k m No power source, transient response depends on initial conditions b B1, B2 depend on initial conditions Equations are the same if: 1/k k b m . I <-> x b . x m or C 1/C R L L R Goal: Simulate the entire system. • Usual practice: – Write all elements as electrical circuit elements. – Represent the intradomain transducers (Ch. 6) – Use the powerful techniques developed for circuit analysis, linear systems (if linear), and feedback control on the whole MEMS system. Senturia generalizes these ideas. • Introduce conjugate power variables, effort, e(t), and flow, f(t). • Then, generalized displacement, q(t) • And generalized momentum, p(t) e . f has units of power e . q has units of energy p . f has units of energy Variable Assignment Conventions • Senturia uses e -> V, that is, effort is linked with voltage in the electrical equivalent circuit. He explains the reasons (for example potential energy is always associated with energy storage in capacitors). Following Senturia’s e -> V convention: • For effort source, e is independent of f • For flow source, f is independent of e • For the generalized resistor, e=e(f) or f=f(e) • Linear resistor e=Rf • Electrical, V=RI • Mechanical, F=bv • For the generalized capacitor (potential energy): •For a linear electrical capacitor: ε – permitivity A – area G – Gap •The mechanical equivalent is the linear spring. (Check in table.) Cspring = 1/k, F=kx •Generalized Inductor or inertance (kinetic energy?) p1 Linear inertance: momentum flow m – mass v – velocity p – momentum momentum? Electrical? But what is this??? ??? v Reluctance q=Ce, e=(1/C)q, Electrical Q=CV (Fmm in example!) (Senturia, not necessary to approximate)