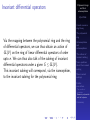
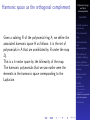
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download PDF Polynomial rings and their automorphisms
Horner's method wikipedia , lookup
Gröbner basis wikipedia , lookup
Ring (mathematics) wikipedia , lookup
Polynomial greatest common divisor wikipedia , lookup
System of polynomial equations wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Factorization wikipedia , lookup
Eisenstein's criterion wikipedia , lookup
Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Polynomial rings and their automorphisms Vipul Naik The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring April 23, 2007 More invariant subrings Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian Further connections A summary A summary What’s a ring Polynomial rings and their automorphisms Vipul Naik A ring is a set R equipped with two binary operations + (addition) and ∗ (multiplication) such that: I (R, +) forms an Abelian group A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary What’s a ring Polynomial rings and their automorphisms Vipul Naik A ring is a set R equipped with two binary operations + (addition) and ∗ (multiplication) such that: I (R, +) forms an Abelian group I (R, ∗) forms a semigroup (that is, ∗ is an associative binary operation) A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary What’s a ring Polynomial rings and their automorphisms Vipul Naik A ring is a set R equipped with two binary operations + (addition) and ∗ (multiplication) such that: I (R, +) forms an Abelian group I (R, ∗) forms a semigroup (that is, ∗ is an associative binary operation) I The following distributivity laws hold: a ∗ (b + c) = (a ∗ b) + (a ∗ c) (a + b) ∗ c = (a ∗ c) + (b ∗ c) The identity element for addition is denoted as 0 and the inverse operation is denoted by the prefix unary −. A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ring with identity Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A ring with identity is a ring for which the multiplication operation has an identity element, that is, there exists an element 1 ∈ R such that: a∗1=1∗a=a ∀ a∈R Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ring with identity Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A ring with identity is a ring for which the multiplication operation has an identity element, that is, there exists an element 1 ∈ R such that: a∗1=1∗a=a ∀ a∈R In other words, the multiplication operation is a monoid operation. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ring with identity Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A ring with identity is a ring for which the multiplication operation has an identity element, that is, there exists an element 1 ∈ R such that: a∗1=1∗a=a ∀ a∈R In other words, the multiplication operation is a monoid operation. Note that in any ring, a ∗ 0 = 0 for all a. Hence, a ring with 1 = 0 must be the trivial ring. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Commutative ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A ring is said to be commutative if the multiplicative operation ∗ is commutative. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Commutative ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A ring is said to be commutative if the multiplicative operation ∗ is commutative. All the rings we shall be looking at today are so-called commutative rings with identity, viz ∗ is commutative and also has an identity element. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Conventions followed while writing expressions in a ring We generally adopt the following conventions: I The multiplication symbol, as well as parentheses for multiplication, are usually omitted. Thus, a ∗ (b ∗ c) may be simply written as abc Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Conventions followed while writing expressions in a ring We generally adopt the following conventions: I I The multiplication symbol, as well as parentheses for multiplication, are usually omitted. Thus, a ∗ (b ∗ c) may be simply written as abc We assume multiplication takes higher precedence over addition. This helps us leave out a number of parentheses. For instance, (a ∗ b) + (c ∗ d) can be written simply as ab + cd Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Conventions followed while writing expressions in a ring We generally adopt the following conventions: I I I The multiplication symbol, as well as parentheses for multiplication, are usually omitted. Thus, a ∗ (b ∗ c) may be simply written as abc We assume multiplication takes higher precedence over addition. This helps us leave out a number of parentheses. For instance, (a ∗ b) + (c ∗ d) can be written simply as ab + cd Parentheses are also dropped from repeated addition Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Conventions followed while writing expressions in a ring We generally adopt the following conventions: I I I I The multiplication symbol, as well as parentheses for multiplication, are usually omitted. Thus, a ∗ (b ∗ c) may be simply written as abc We assume multiplication takes higher precedence over addition. This helps us leave out a number of parentheses. For instance, (a ∗ b) + (c ∗ d) can be written simply as ab + cd Parentheses are also dropped from repeated addition We denote by n ∈ N the number 1 + 1 + 1 . . . 1 where we add 1 to itself n times. Moreover, we denote by nx the number x + x + . . . + x (even when there doesn’t exist any 1) The first of these conventions is justified by associativity of multiplication, the second one is justified by the distributivity law. Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Field Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A field is a very special kind of ring where the nonzero elements form a group under multiplication. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Field Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A field is a very special kind of ring where the nonzero elements form a group under multiplication. Some examples of fields we have seen are Fp (the finite field on p elements), Q (the rationals), R (the reals) and C (the complex numbers). Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Field Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A field is a very special kind of ring where the nonzero elements form a group under multiplication. Some examples of fields we have seen are Fp (the finite field on p elements), Q (the rationals), R (the reals) and C (the complex numbers). An example of a ring which is not a field is Z (the ring of integers). Another is Z/nZ (the ring of integers modulo n). Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Vector space over a field Polynomial rings and their automorphisms Vipul Naik Let k be a field. A vector space over k is a set V equipped with a binary operation + and an operation . : k × V → V such that: I (V , +) is an Abelian group. A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Vector space over a field Polynomial rings and their automorphisms Vipul Naik Let k be a field. A vector space over k is a set V equipped with a binary operation + and an operation . : k × V → V such that: I (V , +) is an Abelian group. I The map . defines a monoid action of the multiplicative monoid of k, over V (as Abelian group automorphisms). In simple language: A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring a.(v + w ) = a.v + a.w a.(b.v ) = (ab).v I For any fixed v ∈ V , the map k → V defined by a 7→ a.v is a group homomorphism Some questions about the invariant subring More invariant subrings Further connections A summary Module over a ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let R be a commutative ring with identity. A module over R is a set M equipped with a binary operation and a map . : R × M → M such that: I (M, +) is an Abelian group. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Module over a ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let R be a commutative ring with identity. A module over R is a set M equipped with a binary operation and a map . : R × M → M such that: I (M, +) is an Abelian group. I The map . defines a monoid action of the multiplicative monoid of R on M Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Generating set for a module Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A set of elements m1 , m2 , . . . , mn is said to be a generating setP for a R-module M if given any m ∈ M, we can express m as i ri mi where ri ∈ R. The elements mi are termed generators. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Generating set for a module Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A set of elements m1 , m2 , . . . , mn is said to be a generating setP for a R-module M if given any m ∈ M, we can express m as i ri mi where ri ∈ R. The elements mi are termed generators. In other words, a generating set is a subset such that every element is a R-linear combination of elements from the subset. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Generating set for a module Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A set of elements m1 , m2 , . . . , mn is said to be a generating setP for a R-module M if given any m ∈ M, we can express m as i ri mi where ri ∈ R. The elements mi are termed generators. In other words, a generating set is a subset such that every element is a R-linear combination of elements from the subset. A R-module that has a finite generating set is termed a finitely generated R-module. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Free generating set Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A generating set m1 , m2 , . . . , mn for a R-module M is termed a free generating set if: X i ri mi = 0 =⇒ ri = 0 ∀ i Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Free generating set Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A generating set m1 , m2 , . . . , mn for a R-module M is termed a free generating set if: X ri mi = 0 =⇒ ri = 0 ∀ i i In other words, there are no unexpected dependencies between the generators. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Free generating set Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A generating set m1 , m2 , . . . , mn for a R-module M is termed a free generating set if: X ri mi = 0 =⇒ ri = 0 ∀ i i In other words, there are no unexpected dependencies between the generators. P In general, dependencies of the form i ri mi = 0 are termed relations, and a relation is trivial if and only if all the ri s are zero. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Irredundant generating set Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A generating set m1 , m2 , . . . , mn for a R-module M is termed irredundant(defined) if no proper subset of it is a generating set. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Irredundant generating set Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A generating set m1 , m2 , . . . , mn for a R-module M is termed irredundant(defined) if no proper subset of it is a generating set. Clearly any free generating set is irredundant, because the ability to express one generator as a linear combination of the others definitely gives a relation. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary In the case of fields Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory In the case of fields, the converse is also true. That is, any irredundant generating set is free. In other words, given any nontrivial relation between the generators, we can express one of the generators in terms of the others. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary In the case of fields Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory In the case of fields, the converse is also true. That is, any irredundant generating set is free. In other words, given any nontrivial relation between the generators, we can express one of the generators in terms of the others. The idea is to pick any generator with a nonzero coefficient, say ri , and multiply the whole equation by 1/ri , and then transfer all the other terms to the right side. We can do this precisely because every nonzero element is invertible. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Vector spaces and free modules Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory For a field, every module (viz vector space) has an irredundant generating set, which is also a free generating set, and in the particular case of fields, we use the term basis(defined) for such a set. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Vector spaces and free modules Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory For a field, every module (viz vector space) has an irredundant generating set, which is also a free generating set, and in the particular case of fields, we use the term basis(defined) for such a set. A module over a ring which possesses a free generating set is termed a free module(defined). Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ring as a module over itself Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Every ring is a module over itself. In fact, when we’re dealing with a ring with identity, it is a free module over itself with the generator being the element 1. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ring as a module over itself Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Every ring is a module over itself. In fact, when we’re dealing with a ring with identity, it is a free module over itself with the generator being the element 1. A submodule of a module is an additive subgroup that is closed under the ring action. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ring as a module over itself Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Every ring is a module over itself. In fact, when we’re dealing with a ring with identity, it is a free module over itself with the generator being the element 1. A submodule of a module is an additive subgroup that is closed under the ring action. An ideal(defined) of a ring is a submodule of the ring when viewed naturally as a module over itself. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Definition of subring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A subset of a ring is said to be a subring if it is a ring with the inherited addition and multiplication operations. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Definition of subring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory A subset of a ring is said to be a subring if it is a ring with the inherited addition and multiplication operations. In the particular case when the whole ring contains an identity element, we typically make the following added assumption about the subring: it contains the identity element of the whole ring. Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms Automorphisms and endomorphisms The notions of invariant subring The fixed-point relationship The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Further connections A summary Definition of polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Let R be a ring. The polynomial ring in one variable, or one indeterminate, is the set of all formal polynomials in one variable, with addition and multiplication defined as usual. The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Definition of polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Let R be a ring. The polynomial ring in one variable, or one indeterminate, is the set of all formal polynomials in one variable, with addition and multiplication defined as usual. We are in particular interested in the polynomial ring in one variable over a field. The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Basic properties of the polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Here are some nice things about the polynomial ring in one variable over a field: I If the product of two polynomials is the zero polynomial, then one of the polynomials must be the zero polynomial. In other words, the product of two nonzero polynomials must be a nonzero polynomial. The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Basic properties of the polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Here are some nice things about the polynomial ring in one variable over a field: I I If the product of two polynomials is the zero polynomial, then one of the polynomials must be the zero polynomial. In other words, the product of two nonzero polynomials must be a nonzero polynomial. The only invertible polynomials in one variable are the constant nonzero polynomials, viz the nonzero polynomials of degree zero The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ideals of the polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring If k is a field, then any ideal in k[x] (viz, any k[x]-submodule of k[x]) is a free module with 1 generator. In other words, it is what is called a principal ideal(defined). The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Ideals of the polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring If k is a field, then any ideal in k[x] (viz, any k[x]-submodule of k[x]) is a free module with 1 generator. In other words, it is what is called a principal ideal(defined). From this, we can in fact deduce the fact that every polynomial over k[x] can be written uniquely as a product of irreducible polynomials, where an irreducible polynomial is one that cannot be factorized further. The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Iterating the polynomial ring operation Polynomial rings and their automorphisms Vipul Naik For any ring R, we can consider the associated polynomial ring R[x1 ]. Setting this as our new ring, we can consider the next associated polynomial, R[x1 ][x2 ], which is basically polynomials with x2 as the indeterminate, over the ring R[x1 ]. We can do this repeatedly and get something called: R[x1 ][x2 ] . . . [xn ] Now, because of the essentially commutative nature of things, we can think of this as simply: R[x1 , x2 , . . . , xn ] viz the polynomial ring in n variables A crash course in ring theory The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Nice properties that continue to hold for many variables Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let k be a field. Then the n-variate polynomial ring over k, viz k[x1 , x2 , . . . , xn ], satisfies the following: I The product of any two nonzero polynomials is nonzero The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Nice properties that continue to hold for many variables Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let k be a field. Then the n-variate polynomial ring over k, viz k[x1 , x2 , . . . , xn ], satisfies the following: I The product of any two nonzero polynomials is nonzero I The only invertible polynomials are the constant nonzero polynomials The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Nice properties that continue to hold for many variables Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let k be a field. Then the n-variate polynomial ring over k, viz k[x1 , x2 , . . . , xn ], satisfies the following: I The product of any two nonzero polynomials is nonzero I The only invertible polynomials are the constant nonzero polynomials I Every polynomial can be factorized uniquely as a product of irreducible polynomials (upto factors of multiplicative constants) The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Nice properties that continue to hold for many variables Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let k be a field. Then the n-variate polynomial ring over k, viz k[x1 , x2 , . . . , xn ], satisfies the following: I The product of any two nonzero polynomials is nonzero I The only invertible polynomials are the constant nonzero polynomials I Every polynomial can be factorized uniquely as a product of irreducible polynomials (upto factors of multiplicative constants) It is not however true that every ideal is principal (we will not delve much into this). The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections The module of covariants Harmonic polynomials and the Laplacian Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary A summary Homomorphism of rings with identity Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let R and S be rings with identity. A homomorphism from R to S is a map f : R → S such that: f (a + b) = f (a) + f (b) f (ab) = f (a)f (b) f (1) = 1 The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Isomorphism, automorphism and endomorphism Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We define: I An isomorphism(defined) is a bijective homomorphism of rings The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Isomorphism, automorphism and endomorphism Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We define: I An isomorphism(defined) is a bijective homomorphism of rings I An endomorphism(defined) is a homomorphism from a ring to itself (need not be injective, surjective or bijective) The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Isomorphism, automorphism and endomorphism Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We define: I An isomorphism(defined) is a bijective homomorphism of rings I An endomorphism(defined) is a homomorphism from a ring to itself (need not be injective, surjective or bijective) I An automorphism(defined) is an isomorphism from a ring to itself, or equivalently, a bijective endomorphism of the ring The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Suffices to locate images of indeterminates Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Let k[x1 , x2 , . . . , xn ] be a polynomial ring, and R be another ring containing a copy of k. Then, the injective homomorphism from k to R can be extended to a homomorphism from k[x1 , x2 , . . . , xn ] to R in many ways. Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Suffices to locate images of indeterminates Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Let k[x1 , x2 , . . . , xn ] be a polynomial ring, and R be another ring containing a copy of k. Then, the injective homomorphism from k to R can be extended to a homomorphism from k[x1 , x2 , . . . , xn ] to R in many ways. In fact, for any choice of elements a1 , a2 , . . . , an ∈ R, there is a unique homomorphism from k[x1 , x2 , . . . , xn ] to R which sends each xi to the corresponding ai . Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Endomorphisms of the polynomial ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let’s now consider the problem of describing all homomorphisms from the polynomial ring k[x1 , x2 , . . . , xn ] to itself, which restrict to the identity on k. The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Endomorphisms of the polynomial ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let’s now consider the problem of describing all homomorphisms from the polynomial ring k[x1 , x2 , . . . , xn ] to itself, which restrict to the identity on k. Here, the ring R is k[x1 , x2 , . . . , xn ] itself. Hence, to specify the endomorphism, we need to give polynomials p1 , p2 , . . . , pn (each being a polynomial in all the xi s) such that each xi maps to the corresponding pi . The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Endomorphisms of the polynomial ring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Let’s now consider the problem of describing all homomorphisms from the polynomial ring k[x1 , x2 , . . . , xn ] to itself, which restrict to the identity on k. Here, the ring R is k[x1 , x2 , . . . , xn ] itself. Hence, to specify the endomorphism, we need to give polynomials p1 , p2 , . . . , pn (each being a polynomial in all the xi s) such that each xi maps to the corresponding pi . Thus, every endomorphism of the polynomial ring (that fixes the base field pointwise) can be described by an arbitrary sequence of n polynomials in the indeterminates. The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Composing two endomorphisms Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The rule for composing endomorphisms of the polynomial ring is as follows: If the endomorphisms are p = (p1 , p2 , . . . , pn ) and q = (q1 , q2 , . . . , qn ) then their composite q ◦ p is the endomorphism The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms xi 7→ qi (p1 (x1 , x2 , . . . , xn ), p2 (x1 , x2 , . . . , xn ), . . . , pn (x1 , x2 , . . . , xn )) The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Composing two endomorphisms Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The rule for composing endomorphisms of the polynomial ring is as follows: If the endomorphisms are p = (p1 , p2 , . . . , pn ) and q = (q1 , q2 , . . . , qn ) then their composite q ◦ p is the endomorphism The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms xi 7→ qi (p1 (x1 , x2 , . . . , xn ), p2 (x1 , x2 , . . . , xn ), . . . , pn (x1 , x2 , . . . , xn )) The notions of invariant subring In particular an endomorphism p is invertible if we can find a q such that (q ◦ p)(xi ) = xi for each i. Some questions about the invariant subring More invariant subrings Further connections A summary Endomorphisms of the polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring In the case of k[x] (polynomial ring in one variable), the endomorphisms are described simply by polynomials. Composition of endomorphisms is, in this context, composition of polynomials. Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Endomorphisms of the polynomial ring in one variable Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring In the case of k[x] (polynomial ring in one variable), the endomorphisms are described simply by polynomials. Composition of endomorphisms is, in this context, composition of polynomials. It’s clear that the only polynomials which have an inverse in the composition sense are the linear polynomials. In other words, the automorphism group of the polynomial ring in one variable is the group of affine maps x 7→ ax + b. Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Affine endomorphisms in more than one variable Polynomial rings and their automorphisms Vipul Naik Given k[x1 , x2 , . . . , xn ] we can consider endomorphisms where all the pi s are linear polynomials in the xi s. This corresponds to affine maps on the vector space k n (basis vectors viewed as xi s) A crash course in ring theory The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Affine endomorphisms in more than one variable Polynomial rings and their automorphisms Vipul Naik Given k[x1 , x2 , . . . , xn ] we can consider endomorphisms where all the pi s are linear polynomials in the xi s. This corresponds to affine maps on the vector space k n (basis vectors viewed as xi s) More specifically, if we consider endomorphisms where all the pi s are homogeneous linear polynomials (viz, linear polynomials without a constant term), we get something which corresponds to linear maps on the vector space k n (basis vectors viewed as xi s) A crash course in ring theory The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Affine endomorphisms in more than one variable Polynomial rings and their automorphisms Vipul Naik Given k[x1 , x2 , . . . , xn ] we can consider endomorphisms where all the pi s are linear polynomials in the xi s. This corresponds to affine maps on the vector space k n (basis vectors viewed as xi s) More specifically, if we consider endomorphisms where all the pi s are homogeneous linear polynomials (viz, linear polynomials without a constant term), we get something which corresponds to linear maps on the vector space k n (basis vectors viewed as xi s) Among these, the invertible elements are precisely those which correspond to invertible affine (respectively linear) maps – viz GAn (k) (respectively GLn (k)). A crash course in ring theory The polynomial ring Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The upshot Polynomial rings and their automorphisms Vipul Naik The upshot is that: A crash course in ring theory The polynomial ring GLn (k) ≤ GAn (k) ≤ Aut(k[x1 , x2 , . . . , xn ]) In other words, every linear automorphism (more generally every affine automorphism) gives rise to a polynomial automorphism, and this association is faithful. Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The upshot Polynomial rings and their automorphisms Vipul Naik The upshot is that: A crash course in ring theory The polynomial ring GLn (k) ≤ GAn (k) ≤ Aut(k[x1 , x2 , . . . , xn ]) In other words, every linear automorphism (more generally every affine automorphism) gives rise to a polynomial automorphism, and this association is faithful. There’s something nice about the polynomial automorphisms that come from linear automorphisms. Namely, these automorphisms actually preserve the degree of the polynomial. Any automorphism that is not linear will not preserve the degree of at least some polynomial. Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring More invariant subrings Further connections A summary The fixed-point relationship Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Given an automorphism σ of the polynomial ring, and a polynomial p that sits inside this polynomial ring, we say that p is a fixed point of σ if σ(p) = p. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring More invariant subrings Further connections A summary The fixed-point relationship Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Given an automorphism σ of the polynomial ring, and a polynomial p that sits inside this polynomial ring, we say that p is a fixed point of σ if σ(p) = p. Thus, given any set P of polynomials p, we can consider the set of all automorphisms σ for which every p ∈ P is a fixed point. This set of automorphisms is clearly a subgroup of the automorphism group. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring More invariant subrings Further connections A summary The fixed-point relationship Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Given an automorphism σ of the polynomial ring, and a polynomial p that sits inside this polynomial ring, we say that p is a fixed point of σ if σ(p) = p. Thus, given any set P of polynomials p, we can consider the set of all automorphisms σ for which every p ∈ P is a fixed point. This set of automorphisms is clearly a subgroup of the automorphism group. Analogously, for every subset S of the automorphism group, we can consider the set Q of all polynomials that are fixed points of every σ ∈ S. Note that this set Q is clearly a ring. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring More invariant subrings Further connections A summary Notion of Galois correspondence Polynomial rings and their automorphisms Vipul Naik The above can be fitted into the framework of a Galois correspondence. Given two sets A and B and a relation R between A and B, the Galois correspondence for R is a pair of maps S : 2A → 2B and T : 2B → 2A defined as: I I A crash course in ring theory The polynomial ring Automorphisms and endomorphisms For C ≤ A, S(C ) is the set of all elements in B that are related to every element in C The notions of invariant subring For D ≤ B, T (D) is the set of all elements in A that are related to every element in D Some questions about the invariant subring Then we have: I C1 ⊆ C2 =⇒ S(C2 ) ⊆ S(C1 ) and similarly for T I S ◦ T ◦ S = S and T ◦ S ◦ T = T The fixed-point relationship More invariant subrings Further connections A summary How this fits in Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory In our case, the relation is the fixed-point relation. That is, the two sets are: I A is the set of all polynomials I B is the group GL(V ) I R is the relation of the given polynomial We are interested in taking subgroups of GL(V ) and asking for the invariant subrings, or conversely, in taking subrings of A and asking for the fixing subgroups. This essentially corresponds to computing the maps T and S. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring More invariant subrings Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Representation of a group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Let G be a group. A linear representation(defined) of G over a field k is a homomorphism ρ : G → GL(V ) where V is a vector space over k and GL(V ) is the group of k-linear automorphisms of V . Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Representation of a group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Let G be a group. A linear representation(defined) of G over a field k is a homomorphism ρ : G → GL(V ) where V is a vector space over k and GL(V ) is the group of k-linear automorphisms of V . The representation is said to be faithful(defined) if ρ is an injective map. In other words, we view G as a subgroup of GL(V ). Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Invariant subring for a representation Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring One of the many aspects to a representation of a group is the following: What is the subring of polynomials that are invariant under the action of the group? In other words, what are the polynomials that are unchanged under the action of the group on the xi s? Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Invariant subring for a representation Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring One of the many aspects to a representation of a group is the following: What is the subring of polynomials that are invariant under the action of the group? In other words, what are the polynomials that are unchanged under the action of the group on the xi s? This is in essence the same as the question we considered earlier. Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Symmetric polynomials Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring A polynomial is said to be a symmetric polynomial(defined) if it remains unchanged under any permutation of the xi s. Clearly, the symmetric polynomials form a subring of the ring of all polynomials. Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Symmetric polynomials Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring A polynomial is said to be a symmetric polynomial(defined) if it remains unchanged under any permutation of the xi s. Clearly, the symmetric polynomials form a subring of the ring of all polynomials. This is precisely the same as the ring of invariant polynomials corresponding to the symmetric group embedded naturally as permutations of the basis elements, in GLn (k). Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Polynomial rings and their automorphisms Elementary symmetric polynomials Vipul Naik A crash course in ring theory The elementary symmetric polynomial of degree j over variables x1 , x2 , . . . , xn is defined as the coefficient of x n−j in the expression: Y (x + xi ) Or equivalently, Q as expression i (x − xi ). times the coefficient of Automorphisms and endomorphisms The notions of invariant subring i (−1)j The polynomial ring x n−j in the Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Polynomial rings and their automorphisms Elementary symmetric polynomials Vipul Naik A crash course in ring theory The elementary symmetric polynomial of degree j over variables x1 , x2 , . . . , xn is defined as the coefficient of x n−j in the expression: Y (x + xi ) Automorphisms and endomorphisms The notions of invariant subring i (−1)j The polynomial ring x n−j Or equivalently, times the coefficient of Q as expression i (x − xi ). We shall use the letter sj to denote the elementary symmetric polynomial of degree j. in the Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Two remarkable facts It is clear that any elementary symmetric polynomial is a symmetric polynomial. Thus, any polynomial in terms of the elementary symmetric polynomials also is an elementary symmetric polynomial. In other words, we have a homomorphism: k[s1 , s2 , . . . , sn ] → k[x1 , x2 , . . . , xn ]Sn Two remarkable facts are: I This mapping is injective. That is, any two different polynomials in the sj s give rise to different polynomials in the xi s. Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Two remarkable facts It is clear that any elementary symmetric polynomial is a symmetric polynomial. Thus, any polynomial in terms of the elementary symmetric polynomials also is an elementary symmetric polynomial. In other words, we have a homomorphism: k[s1 , s2 , . . . , sn ] → k[x1 , x2 , . . . , xn ]Sn Two remarkable facts are: I I This mapping is injective. That is, any two different polynomials in the sj s give rise to different polynomials in the xi s. This mapping is surjective. That is, any symmetric polynomial in the xi s can be expressed as a polynomial in the sj s. Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Generating set for an algebra Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory What we have done is shown that the invariant subring for the symmetric group is in fact itself isomorphic to a polynomial ring, in other words, we can find polynomials in it such that this subring is generated by these polynomials, without any further relations between them. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Generating set for an algebra Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory What we have done is shown that the invariant subring for the symmetric group is in fact itself isomorphic to a polynomial ring, in other words, we can find polynomials in it such that this subring is generated by these polynomials, without any further relations between them. This gives some notions. Let k be a base field. Then any ring R containing k is termed a k-algebra. A generating set for R is a set S such that every element of R can be expressed as a polynomial in elements of S with coefficients from k. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Generating set (continued) Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory I An algebra over k is said to be finitely generated(defined) if it has a finite generating set as a k-algebra, that is, there is a surjective homomorphism to it from the polynomial ring in finitely many variables The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Generating set (continued) Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory I I An algebra over k is said to be finitely generated(defined) if it has a finite generating set as a k-algebra, that is, there is a surjective homomorphism to it from the polynomial ring in finitely many variables An algebra over k is said to be free(defined) if we can find a generating set such that the mapping from the polynomial ring of that generating set to the given algebra, is an isomorphism. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Two questions of interest Polynomial rings and their automorphisms Vipul Naik Given a group G and a (without loss of generality, faithful) linear representation of G of degree n, let R = k[x1 , x2 , . . . , xn ]G be the invariant subring corresponding to G . Two questions we are interested in are: I Is R a finitely generated k-algebra? A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Two questions of interest Polynomial rings and their automorphisms Vipul Naik Given a group G and a (without loss of generality, faithful) linear representation of G of degree n, let R = k[x1 , x2 , . . . , xn ]G be the invariant subring corresponding to G . Two questions we are interested in are: I Is R a finitely generated k-algebra? I Is R a free k-algebra? That is, can R be viewed as the polynomial ring in some number of variables? In the case where G is the symmetric group, the answer to both questions was yes, the elementary symmetric polynomials formed a finite freely generating set for R. A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Definition of the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The orthogonal group of order n over a field k, denoted as On (k), is defined as the group of those matrices A such that AAT is the identity matrix. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Definition of the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The orthogonal group of order n over a field k, denoted as On (k), is defined as the group of those matrices A such that AAT is the identity matrix. Equivalently, it is the group of those transformation of the space k n that fix the origin and the norm of any P preserve 2 vector, that is, they preserve i xi for any vector (x1 , x2 , . . . , xn ). Equivalently, it is the group of those transformations of the space k n that preserve the scalar product of any two vectors. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Invariant polynomials for the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory 2 i xi P Clearly, the polynomial is an invariant polynomial under the action of the orthogonal group. Hence, the invariant subring P contains, as a subring, the polynomial ring generated by i xi2 . The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Invariant polynomials for the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory 2 i xi P Clearly, the polynomial is an invariant polynomial under the action of the orthogonal group. Hence, the invariant subring P contains, as a subring, the polynomial ring generated by i xi2 . It turns out that the converse is also true: any polynomial in the xi s that is invariant under the actionPof the orthogonal group must actually be a polynomial in i xi2 . The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary A closer inspection of the orthogonal group action Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The orthogonal group acts on the space k n , and k n naturally decomposes into orbits under the action. Since every element P 2 of the orthogonal group preserves the polynomial Pi xi2 , each orbit must lie inside a “sphere” of the form i xi = c for some value of c. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary A closer inspection of the orthogonal group action Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The orthogonal group acts on the space k n , and k n naturally decomposes into orbits under the action. Since every element P 2 of the orthogonal group preserves the polynomial Pi xi2 , each orbit must lie inside a “sphere” of the form i xi = c for some value of c. It turns out that the action is also transitive, i.e. given any two points on the same sphere, there is an element of the orthogonal group taking one to the other. This essentially follows from the fact that any unit vector can be completed to an orthonormal basis. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary The proof for the invariant subring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Proving P 2 that the invariant subring comprises polynomials in i xi thus reduces to proving that: Any polynomial P 2 that is constant on spheres (that P is,2 loci of the form i xi = c) must be a polynomial in i xi . The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary The proof for the invariant subring Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Proving P 2 that the invariant subring comprises polynomials in i xi thus reduces to proving that: Any polynomial P 2 that is constant on spheres (that P is,2 loci of the form i xi = c) must be a polynomial in i xi . We’ll prove a more general statement: Let p be a polynomial in x1 , x2 , . . . , xn . Any polynomial f such that f is constant on each locus p(x) = c (i.e. p(x) = p(y ) =⇒ f (x) = f (y )) must itself be a polynomial in p. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Proof of the general statement Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We write x for the tuple (x1 , x2 , . . . , xn ). Consider the locus p(x) = c. Suppose f (x) takes the value λ on this locus. Then, by the factor theorem: f (x) − λ = h(x)(p(x) − c) where h(x) is another polynomial. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Proof of the general statement Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We write x for the tuple (x1 , x2 , . . . , xn ). Consider the locus p(x) = c. Suppose f (x) takes the value λ on this locus. Then, by the factor theorem: f (x) − λ = h(x)(p(x) − c) where h(x) is another polynomial. Now, h also satisfies the property of being constant on every locus p(x) = c 0 . By induction, we can write h as a polynomial in p, and hence f can also be written as a polynomial in p. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Upshot: for the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring We have shown that for the orthogonal group, the invariant subring is in fact the polynomial ring in one variable. Hence, it is both free and finitely generated. Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Polynomial rings and their automorphisms Orbits as sets of constancy Vipul Naik kn If G ≤ GL(V ), then any orbit of under the action of G , must take a constant value under any polynomial invariant under the action of G . In other words, we can define two relations: I I Given a subring R of the polynomial ring, call x, y ∈ k n as R-equivalent if f (x) = f (y ) for any f ∈ R kn Given a group G ≤ GL(V ), call x, y ∈ as G -equivalent if there exists g ∈ G such that g .x = y Then if R is the invariant subring for G , G -equivalence implies R-equivalence. A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Rings of constant functions versus ideals Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Given a subset S ⊆ k n , define I (S) as the set of all polynomials that vanish at every point of S, and R(S) as the ring of all polynomials that are constant on S. Then: The polynomial ring Automorphisms and endomorphisms The notions of invariant subring R(S) = I (S) + k In other words, every polynomial constant on S can be written as a polynomial that vanishes on S, plus a constant polynomials. Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Expression for the invariant subring Polynomial rings and their automorphisms Vipul Naik Here’s the chain of reasoning: I Any polynomial invariant under the action of G must be constant on all the G -orbits A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Expression for the invariant subring Polynomial rings and their automorphisms Vipul Naik Here’s the chain of reasoning: A crash course in ring theory I Any polynomial invariant under the action of G must be constant on all the G -orbits I Hence, it is the intersection, over each orbit O of G , of the ring of polynomials constant on O, viz R(O): k[x1 , x2 , . . . , xn ]G = \ R(O) O I Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Since R(O) = I (O) + k, we get: k[x1 , x2 , . . . , xn ]G = The polynomial ring \ O I (O) + k The orthogonal group Relation between invariant polynomials and vanishing sets Further connections A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The module of covariants Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The setup so far is: I The algebra A = k[x1 , x2 , . . . , xn ] The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The module of covariants Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The setup so far is: I The algebra A = k[x1 , x2 , . . . , xn ] I A group G acting on GL(V ) and hence acting as algebra automorphisms of k[x1 , x2 , . . . , xn ] I R = AG is the subring comprising invariant polynomials Since A is a ring containing R, A is a R-algebra, and in particular, A is also a R-module. A, viewed as a R-module, is termed the module of covariants(defined). The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Two natural questions Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Using the setup and notation of the previous question: I I When is the module of covariants free? That is, under what conditions is it true that A is a free R-module? When is the module of covariants finitely generated? That is, under what conditions is it true that A is a finitely generated R-module? Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Relating covariants with invariants Polynomial rings and their automorphisms Vipul Naik A remarkable result states that for representations of finite groups, the module of covariants is free if and only if the algebra of invariants is free (as an algebra). A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Relating covariants with invariants Polynomial rings and their automorphisms Vipul Naik A remarkable result states that for representations of finite groups, the module of covariants is free if and only if the algebra of invariants is free (as an algebra). For instance, in the case of the symmetric group, the algebra of invariants is freely generated by the elementary symmetric polynomials, and the module of covariants is free (the latter is not at all obvious). A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Relating covariants with invariants Polynomial rings and their automorphisms Vipul Naik A remarkable result states that for representations of finite groups, the module of covariants is free if and only if the algebra of invariants is free (as an algebra). For instance, in the case of the symmetric group, the algebra of invariants is freely generated by the elementary symmetric polynomials, and the module of covariants is free (the latter is not at all obvious). Kostant looked at the problem of freeness of the module of covariants for the module of covariants, in the case of a connected infinite group, and came up with certain sufficient conditions. A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The differential operator corresponding to a polynomial Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Given any polynomial p in variables x1 , x2 , . . . , xn , we can associate a corresponding linear differential operator, ∂ obtained by replacing each xi by the expression ∂x . i Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The differential operator corresponding to a polynomial Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Given any polynomial p in variables x1 , x2 , . . . , xn , we can associate a corresponding linear differential operator, ∂ obtained by replacing each xi by the expression ∂x . i In fact, this gives an isomorphism between the polynomial ring in n variables and the ring of partial linear differential operators of order upto n, with multiplication being composition (note that this is a commutative ring because partials commute). Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Invariant differential operators Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Via the mapping between the polynomial ring and the ring of differential operators, we can thus obtain an action of GL(V ) on the ring of linear differential operators of order upto n. We can thus also talk of the subring of invariant differential operators under a given G ≤ GL(V ). Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Invariant differential operators Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Via the mapping between the polynomial ring and the ring of differential operators, we can thus obtain an action of GL(V ) on the ring of linear differential operators of order upto n. We can thus also talk of the subring of invariant differential operators under a given G ≤ GL(V ). This invariant subring will correspond, via the isomorphism, to the invariant subring for the polynomial ring. Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The particular case of the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The ring of invariant polynomials P under the action of the orthogonal group is generated by i xi2 . The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary The particular case of the orthogonal group Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The ring of invariant polynomials P under the action of the orthogonal group is generated by i xi2 . Correspondingly, the ring of invariant differential operators under the action of the orthogonal group is generated by the differential operator: X ∂2 ∆= ∂xi2 i This is the famous Laplacian. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Polynomial rings and their automorphisms Harmonic polynomials A polynomial f in n variables is termed a harmonic polynomial(defined) if its Laplacian is zero. That is, f is harmonic if the polynomial: n X ∂2f i=1 ∂xi2 is identically the zero polynomial. Some examples of harmonic polynomials: I Any linear polynomial is harmonic. Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Polynomial rings and their automorphisms Harmonic polynomials A polynomial f in n variables is termed a harmonic polynomial(defined) if its Laplacian is zero. That is, f is harmonic if the polynomial: n X ∂2f i=1 ∂xi2 is identically the zero polynomial. Some examples of harmonic polynomials: I Any linear polynomial is harmonic. I More generally, any multilinear polynomial is harmonic. In fact, the partial derivative in each of the xi s for a multilinear polynomial, is zero (note that the property of being multilinear is not invariant under the action of GL(V ), though the property of being linear is) Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Polynomial rings and their automorphisms A bilinear map Vipul Naik Let A denote the ring of polynomials, and à denote the ring of differential operators. Since any differential operator acts on a polynomial and outputs a polynomial, we have a map: Ã × A → A This map is a k-bilinear map, that is, it is k-linear in both variables. A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Polynomial rings and their automorphisms A bilinear map Vipul Naik Let A denote the ring of polynomials, and à denote the ring of differential operators. Since any differential operator acts on a polynomial and outputs a polynomial, we have a map: Ã × A → A This map is a k-bilinear map, that is, it is k-linear in both variables. ∂ Now, the mapping xi 7→ ∂x gives an isomorphism: i D:A∼ = à Under this identification, we get in essence a map: D1 : A × A → A A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary which is k-bilinear. Harmonic space as the orthogonal complement Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory Given a subring R of the polynomial ring A, we define the associated harmonic space H as follows: it is the set of polynomials in A that are annihilated by R under the map D1 . This is a k-vector space by the bilinearity of the map. The harmonic polynomials that we saw earlier were the elements in the harmonic space corresponding to the Laplacian. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Outline A crash course in ring theory Definition of ring Modules over rings Generating sets and bases Rings and ideals Concept of subring The polynomial ring The polynomial ring in one variable The polynomial ring in many variables Automorphisms and endomorphisms Homomorphism of rings Homomorphisms from the polynomial ring Linear and affine endomorphisms Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring Automorphisms and endomorphisms The notions of invariant subring The notions of invariant subring The fixed-point relationship Some questions about the invariant subring Some questions about the invariant subring Representations and faithful representations Generating sets and questions More invariant subrings More invariant subrings The orthogonal group Relation between invariant polynomials and vanishing sets Further connections The module of covariants Harmonic polynomials and the Laplacian A summary Further connections A summary The overall setup Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We were looking at: I The ring A of polynomials over k in n variables The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The overall setup Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We were looking at: I The ring A of polynomials over k in n variables I A group G acting on A The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The overall setup Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We were looking at: I The ring A of polynomials over k in n variables I A group G acting on A I The invariant subring R = AG of A under the action of G We considered these questions: I As a k-algebra, is R free and is it finitely generated? The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The overall setup Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory We were looking at: I The ring A of polynomials over k in n variables I A group G acting on A I The invariant subring R = AG of A under the action of G We considered these questions: I As a k-algebra, is R free and is it finitely generated? I As a R-module, is A free and is it finitely generated? The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The tools we used Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory While studying this question, one useful approach was to think of G acting on k n with a certain orbit decomposition, and to view the polynomials as functions of k n . In particular, this forced the invariant polynomials to become constant functions on each orbit. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The tools we used Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory While studying this question, one useful approach was to think of G acting on k n with a certain orbit decomposition, and to view the polynomials as functions of k n . In particular, this forced the invariant polynomials to become constant functions on each orbit. We also used the fact that every polynomial can be naturally identified with a corresponding differential operator, and used this to construct a bilinear map from the space of polynomials to itself. The polynomial ring Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The particular cases Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring I For the symmetric group, we saw that the invariant subring is a free algebra with generating set being the elementary symmetric polynomials. Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The particular cases Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring I I For the symmetric group, we saw that the invariant subring is a free algebra with generating set being the elementary symmetric polynomials. For the orthogonal group, we saw that the invariant subring is a free algebra with generating set being the sum of squares polynomial Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary The particular cases Polynomial rings and their automorphisms Vipul Naik A crash course in ring theory The polynomial ring I I For the symmetric group, we saw that the invariant subring is a free algebra with generating set being the elementary symmetric polynomials. For the orthogonal group, we saw that the invariant subring is a free algebra with generating set being the sum of squares polynomial Automorphisms and endomorphisms The notions of invariant subring Some questions about the invariant subring More invariant subrings Further connections A summary