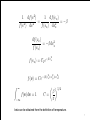* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Class 3
Survey
Document related concepts
Transcript
Thermodynamics Class 3
Previous class: the microscopic view of ideal gas “Temperature”
!
1, <w.vcm> = <[(m1v12-m2v22)+(m2-m1)(v1.v2)]/(m1+m2)>.
3/2 kT = <1/2 mv2>, proportional to the average molecule kinetic energy
!
2, Ideal gas law, PV=µRT
!
3, Van der Waals law for real gas: [P+a(µ/V)2][V-µb]=µRT.
!
4, dP = - nmg dh => n = n0 exp(- P.E. / kT) Boltzmann’s law
!
!1
Questions from the last class:
!
a): <w.vcm> = 0?
<w.vcm> = sum_{ijk} wi vcmj cosθk / N. θk is independent of wi and vcmj. And
sum_k cosθk = 0.
!
!2
!3
The distribution of molecular speeds
It’s important to know the velocity distribution. For example, we can calculate the
average speed, thermal velocity, etc from the distribution function.
!
Now let’s consider the distribution of molecules in an atmosphere.
!
At height h, the number of molecules that pass upward though the lower plane in a
vertical direction with velocity component greater than u is exactly the same as the
number which pass through the upper plane with any upward velocity.
!
nvz>=0(h) = nvz>=u(0), with 1/2mu2 = mgh
!
So nvz>=u(0) / nvz>0(0) = exp(-1/2 mu2/kT) or
!
n >u is proportional to exp(-K.E./kT)
!
Z 1
2
uf (u)du = C exp( 1/2mu /kT )
u
2
f (u)du = C exp[ (1/2)mu /kT ]
!4
The distribution of molecular speeds (cont’d)
To get the normalisation coefficient, we have C = sqrt(m/2pi kT), using
Z
1
e
x2
dx =
p
⇡
1
So the distribution of velocity is f du = C exp(-K.E./kT).
!
If written in momentum which is also valid in relativity, f(p) dp = C exp(-K.E./kT) dp.
!
Note that both the spatial and the velocity distribution has the form of exp(-energy /
kT).
!
Generalize to three dimensions, we have
f (vx , vy , vz )dvx dvy dvz / e
2
mvx
/2kT
e
mvy2 /2kT
e
mvz2 /2kT
!5
A more formal way of showing the velocity distribution in thermal
equilibrium.
Maxwell assumed that in thermal equilibrium, f is a function of v only. f(vx), f(vy) and
f(vz) are independent of each other. We can derive the form of f(vx, vy, vz) like this.
!
f(v) is independent of the direction of v.
2
f (vx , vy , vz ) = f (v ) = f (vx )f (vy )f (vz )
@f (v 2 )
df (v 2 ) @v 2
df (v 2 )
df (vx )
=
= 2vx
=
f (vy )f (vz )
2
2
@vx
dv @vx
dv
dvx
df (v 2 )
df (vx )
=
f
(v
)f
(v
)
y
z
dv 2
dvx2
1 df (v 2 )
1 df (vx )
=
f (v 2 ) dv 2
f (vx ) dvx2
!6
1 df (v 2 )
1 df (vx )
=
=
f (v 2 ) dv 2
f (vx ) dvx2
df (vx )
=
f (vx )
2
dvx
f (vx ) = C1 e
f (v) = Ce
Z
1
1
f (v)dv = 1
2
vx
2
(vx
+vy2 +vz2 )
C=
✓ ◆3/2
⇡
beta can be obtained from the definition of temperature.
!7
Degrees of freedom
The degrees of freedom: the minimum number of independent coordinates that
can specify the position of the system completely.
!
Monoatomic molecules: H, O, 3 degrees of freedom
Diatomic molecules: 3 translational motion (x,y,z) + 2 rotational motion (ignoring
the rotation along the line connecting the two atoms) + 1 vibrational motion (the
distance between two atoms) = 6 degrees of freedom
!
In general, for a n-atom molecule: 3n degrees of freedom. Each atom needs
three coordinates.
!
In these 3n: 3 translational motion of the molecule as a whole.
3 rotational motion as a whole if not all the atoms are collinear.
So there are 3n-6 degrees of freedom for vibrational motion.
!
If all the atoms are collinear (e.g., a diatomic molecule), then there are 2
rotational degrees of freedom. and 3n-(3+2) = 3n-5 degrees of vibrational
freedom.
!8
Equipartition of energy (Equipartition Theorem)
Suppose the kinetic energy of a molecule is
K.E. =
N
X
1
2
i=1
2
mvi
N
Y
1
f (v1 , v2 , v3 , ..., vN ) / exp( K.E./kT ) =
exp(
mvi2 /kT )
2
i=1
1
2
mv
i
2
write exp(
Z
kT
r
1
1
exp(
⇡
2
Z
1
x )dx =
1
r
2
vi )
) as exp(
1
mvi2 exp(
2
⇡
Z
1
1
with
vi2 )dvi
2
x exp(
=
kT
1
= kT
2
1
x )dx =
2
2
1
2m
r
⇡
3
So we have that the average kinetic energy of every degree of freedom is equal to 1/2 kT.
!9
For vibrational motion, we also have potential energy. If it’s a harmonic
oscillator, then <P.E.> = <K.E.>
!
For a monoatomic gas: we have U = N (3/2) kT (3 degrees of
translational motion.
!
For a diatomic gas: we have U = N * (3/2 + 2/2 + 1/2 + 1/2) kT = N 7/2
kT.
!
PV = NkT = (ɣ-1)U
!
So for a monoatomic gas: NkT = 2/3 U => ɣ = 5/3 ~ 1.667
For a diatomic gas: NkT = 2/7 U => ɣ = 9/7 ~ 1.286.
!10
!11
Fig. 40–6.Experimental values of γ as a function of
temperature for hydrogen and oxygen. Classical theory
predicts γ=1.286, independent of temperature.
!12
Failure of classical physics
For diatomic gases like H2 or O2, we assumed that the vibrational motion is like a
harmonic oscillator. What if that’s not true? If the coupling between two atoms is very
rigid, and there is no vibration, then we will have U = (3/2+2/2) kT = 5/2 kT and ɣ =
7/5 =1.4。This looks quite close to experimental results. But ɣ varies with
temperature for both H2 and O2.
!
It seems like as the temperature falls, certain kinds of motion “freeze out”.
!
This represents the failure of classical physics.
The resolution is in Quantum Mechanics.
!
In QM, the energy of a harmonic oscillator is not continuous, but is quantized. While in
classical physics, it is continuous.
!
For a harmonic oscillator, its energy levels are
Pn
e
=
P0
e
En /kT
E0 /kT
=e
n~!/kT
nn
=
n0
!13
Failure of classical physics (cont’d)
n = n0 e
So that
If
E/kT
with E varies from 0 to 1
R1
EndE
0
hEi = R 1
= kT
ndE
0
kT ⌧ ~! , then all atoms are in the lowest energy level.
The contribution of the harmonic oscillator to the total energy of the molecule is negligible.
!14