Download Oops !Power Point File of Physics 2D lecture for Today should have

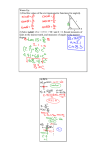
Physics 2D Lecture Slides
Mar 10
Vivek Sharma
UCSD Physics
QM in 3 Dimensions
• Learn to extend S. Eq and its
solutions from “toy” examples
in 1-Dimension (x)  three
orthogonal dimensions
(rx,y,z)
ˆ
ˆ  ˆjy  kz
r  ix
• Then transform the systems
– Particle in 1D rigid box  3D
rigid box
– 1D Harmonic Oscillator  3D
Harmonic Oscillator
z
• Keep an eye on the number
of different integers needed
to specify system 1 3
(corresponding to 3 available
degrees of freedom x,y,z)
y
x
Quantum Mechanics In 3D: Particle in 3D Box
z
Extension of a Particle In a Box with rigid walls
1D  3D
 Box with Rigid Walls (U=) in
X,Y,Z dimensions
z=L
U(r)=0 for (0<x,y,z,<L)
Ask same questions:
• Location of particle in 3d Box
• Momentum
• Kinetic Energy, Total Energy
• Expectation values in 3D
y
y=0
y=L
x
To find the Wavefunction and various
expectation values, we must first set up
the appropriate TDSE & TISE
The Schrodinger Equation in 3 Dimensions: Cartesian Coordinates
Time Dependent Schrodinger Eqn:

2
2m
 2  ( x, y , z , t )  U ( x, y , z )  ( x, t )  i
 ( x, y, z , t )
.....In 3D
t
2
2
2
  2 2 2
x y z
2
z
2
2
2

2  
2  
2 
So 
  
 

 [K ]
2  
2 
2 
2m
 2m x   2m y   2m z 
=
[K x ]
+
[K y ] + [K z ]
2
2
y
x
so [ H ] ( x, t )  [ E ] ( x, t ) is still the Energy Conservation Eq
Stationary states are those for which all probabilities are constant in time
and are given by the solution of the TDSE in seperable form:
 ( x, y, z , t )   (r , t ) = (r)e -i t
This statement is simply an extension of what we derived in case of 1D
time-independent potential
Particle in 3D Rigid Box : Separation of Orthogonal Spatial (x,y,z) Variables
2
TISE in 3D: -
 2 ( x, y, z )  U ( x, y, z ) ( x, y, z )  E ( x, y, z )
2m
x,y,z independent of each other , write  ( x, y, z )   1 ( x) 2 ( y) 3 ( z )
and substitute in the master TISE, after dividing thruout by = 1 ( x) 2 ( y ) 3 ( z )
and noting that U(r)=0 for (0<x,y,z,<L) 
2
2
2

1  2 1 ( x)  
1  2 2 ( y )  
1  2 3 ( z ) 
  E  Const



2
2
2
 2m  1 ( x) x   2m  2 ( y ) y
  2m  3 ( z ) z

This can only be true if each term is constant for all x,y,z 
2
2
 2 3 ( z )
 2 1 ( x)
 2 2 ( y )

 E1 1 ( x) ; 
 E2 2 ( y ) ; 
 E3 3 ( z )
2
2
2
2m x
2m y
2m z
2
With E1  E 2  E 3  E=Constant
(Total Energy of 3D system)
Each term looks like particle in 1D box (just a different dimension)
So wavefunctions must be like  1 ( x)  sin k1x ,  2 ( y )  sin k2 y ,  3 ( z )  sin k3 z
Particle in 3D Rigid Box : Separation of Orthogonal Variables
Wavefunctions are like  1 ( x)  sin k1x ,  2 ( y )  sin k2 y ,  3 ( z )  sin k3 z
Continuity Conditions for  i and its first spatial derivatives  ni  ki L
Leads to usual Quantization of Linear Momentum p= k .....in 3D

px  
 L

 
 
 n1 ; p y  
 n2 ; pz  
 n3 (n1 , n 2 , n 3  1, 2,3,..)

 L 
 L 
Note: by usual Uncertainty Principle argument neither of n1 , n 2 , n 3  0! ( why ?)
1
2 2 2 2 2
2
2
2
Particle Energy E = K+U = K +0 =
( px  p y  pz ) 
(n1  n2  n3 )
2
2m
2mL
Energy is again quantized and brought to you by integers n1 , n 2 , n 3 (independent)
and  (r)=A sin k1x sin k2 y sin k3 z (A = Overall Normalization Constant)
 (r,t)= (r) e
E
-i t
 A [sin k1x sin k2 y sin k3 z ] e
E
-i t
Particle in 3D Box :Wave function Normalization Condition
 (r,t)= (r) e
E
-i t
 * (r,t)= * (r) e
 A [sin k1x sin k2 y sin k3 z ] e
E
i t
E
-i t
 A [sin k1x sin k2 y sin k3 z ] e
E
i t
 * (r,t) (r,t)=A2 [sin 2 k1x sin 2 k2 y sin 2 k3 z ]
Normalization Condition : 1 =
 P(r)dx dydz

x,y,z
 L  L  L 
1  A  sin k1x dx  sin k2 y dy  sin k3z dz = A 





x=0
y=0
z=0
 2  2  2 
L
L
2
2
3
2
2
 A    and  ( r,t)=
L
L
2
2
3
2
2
E
i
t
2
 
 L  [sin k1x sin k2 y sin k3 z ] e
Particle in 3D Box : Energy Spectrum & Degeneracy
E n1 ,n 2 ,n 3 
2
2
2
2mL
( n12  n22  n32 ); n i  1, 2, 3..., ni  0
Ground State Energy E111
3 2 2

2mL2
6 2 2
Next level  3 Excited states E 211 = E121  E112 
2mL2
Different configurations of  (r)= (x,y,z) have same energy  degeneracy
z
z=L
y=L y
x=L
x
Degenerate States
E 211 = E121  E112
Ground State
6 2 2

2mL2
E111


z
z
y
y
x
x
E211
E121
E112
Probability Density Functions for Particle in 3D Box
Same Energy  Degenerate States
Cant tell by measuring energy if particle is in
211, 121, 112 quantum State
• Degeneracy came from the
threefold symmetry of a
CUBICAL Box (Lx= Ly= Lz=L)
• To Lift (remove) degeneracy 
change each dimension such that
CUBICAL box  Rectangular
Box
• (Lx Ly  Lz)
• Then
 n12 2 2   n22 2 2   n32 2 2 
E 


2  
2 
2 


2
mL
2
mL
2
mL
x  
y 

z 

Energy
Source of Degeneracy: How to “Lift” Degeneracy
The Hydrogen Atom In Its Full Quantum Mechanical Glory
U (r ) 
r
1

r
1
x y z
2
2
2
 More complicated form of U than box
By example of particle in 3D box, need to use seperation of
variables(x,y,z) to derive 3 independent differential. eqns.
This approach will get very ugly since we have a "conjoined triplet"
To simplify the situation, use appropriate variables
Independent Cartesian (x,y,z)  Inde. Spherical Polar (r, , )
2
2
2
Instead of writing Laplacian   2  2  2 , write
x y z
2
1   2  
1
 
 
1
2
 = 2 r
 2
 sin 
 2 2
r r  r  r sin   
  r sin   2
2
TISE for  (x,y,z)= (r, , ) becomes
kZe2
U (r ) 
r
1   2  (r, , ) 
1
 
 (r, , ) 
r

sin


 2


2
r r 
r

 r sin   

1
 2 (r, , ) 2m
+ 2 (E-U(r)) (r, , ) =0
r 2 sin 2 
 2
!!!! fun!!!
Spherical Polar Coordinate System
Volume Element dV
dV  (r sin  d )(rd )(dr )
= r 2 sin  drd d
Don’t Panic: Its simpler than you think !
1   2  
1
 
 
1
 2 2m
+ 2 (E-U(r)) (r, , ) =0
r

 sin 

r 2 r 
r  r 2 sin   
  r 2 sin 2   2
Try to free up last term from all except 
This requires multiplying thruout by r 2 sin 2  
  2  
 
   2 2mr 2 sin 2 
ke 2
sin 
+
(E+
) =0
r
  sin 
 sin 

2
r 
r 
 
   2
r
For Seperation of Variables, Write  (r, , )=R(r).( ). ( )
2
Plug it into the TISE above & divide thruout by  (r, , )=R(r).( ). ( )
Note that :
 ( r ,  ,  )
R(r)
 ( ). ( )
r
r
 ( r ,  ,  )
( )
 R ( r ) ( )
 when substituted in TISE


 ( r ,  ,  )
 ( )
 R ( r )( )


sin 2    2 R  sin   
  1  2  2mr 2 sin 2 
ke 2
+
(E+
) =0
r

 sin 

2
R r 
r 
  
    2
r
Rearrange by taking the  term on RHS
sin 2    2 R  sin   
  2mr 2 sin 2 
ke 2
1  2
(E+
) =r

 sin 
+
2
R r 
r 
  
 
r
  2
LHS is fn. of r, & RHS is fn of  only , for equality to be true for all r, , 
 LHS= constant = RHS = ml2
Now go break up LHS to seperate the r &  terms.....
sin 2    2 R  sin   
  2mr 2 sin 2 
ke 2
LHS:
(E+
) =ml2
r

 sin 
+
2
R r  r 
  
 
r
Divide Thruout by sin 2 and arrange all terms with r away from  
ml2
1   2 R  2mr 2
ke 2
1
 
 
)= 2 
r
  2 (E+
 sin 

R r  r 
r
sin   sin   
 
Same argument : LHS is fn of r, RHS is fn of  , for them to be equal for all r,
 LHS = const = RHS = l (l  1)
What do we have after shuffling!
d 2
2

m
  0...................(1)
l
2
d
ml2 
1 d 
d  
 sin 
  l (l  1)  2  ( )  0.....(2)
sin  d 
d  
sin  
1 d  2 R   2mr 2
ke 2 l (l  1) 
)R(r )  0....(3)
r
   2 (E+

2
2
r dr  r  
r
r 
These 3 "simple" diff. eqn describe the physics of the Hydrogen atom.
All we need to do now is guess the solutions of the diff. equations
Each of them, clearly, has a different functional form