Download Changing a matrix to echelon form

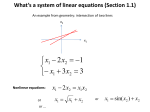
Definitions and algorithms for solving linear systems
A system of equations is in echelon form provided
1) Each equation’s leading coefficient is 1.
2 ) Each equation’s leading term is strictly to the right of the leading term in
the equation above.
X + 2y + 3z + w = 19
Z +7w = 9
W = 123
W = 123
Z = 9 -7w=9-7(123) = -852
Y = r (arbitrary)
X = 19 – 2y – 3z – w = whatever.
To solve a linear system in echelon form:
1) Circle the leading variable in each equation.
2) List and solve for the unknowns in reverse order.
a) If an unknown is uncircled, it is arbitrary
b) If an unknown is circled, solve for it in the equation that contains it as
a leading variable.
It’s easier to work with the augmented matrix of a system, obtained by
erasing the variables and the equals signs.
1X + 2y + 3z + w = 19
1Z +7w = 9
1W = 123
1 2 3 1 19
0 0 1 7
9
0 0 0 1 123
3 equations, 4 unknowns
Aug matrix 3 rows, 5 column
A matrix is in echelon form provided:
The leftmost nonzero entry in each row is 1. This entry is called a leading 1.
The leading 1 in any row is strictly to the right of the leading 1 in any row
above.
A matrix is in reduced echelon form provided
It is in echelon form AND
Each leading 1 is the only nonzero entry in its column.
Elementary Row Ops:
Type I: Exchange Ri and Rj.
Type II: Multiply any row Ri by a nonzero constant.
Type III: Replace Ri by Ri + cRj.
Algorithm: To change a matrix to echelon form:
Step 1. Exchange rows, if necessary to bring the leftmost nonzero entry to
the top row.
Step 2. Divide Row 1 by its leftmost nonzero entry to get a leading 1.
Step 3. Use Type 3 ops to change all entries beneath that leading 1 to 0.
Repeat the above 3 steps to the matrix consisting of rows below the top row.
Variant: To change the matrix to reduced echelon form,
Step 4: Use Type 3 ops to change all entries above the leading 1 to 0.
To solve a linear system by Gauss (Gauss-Jordan) Elimination:
Step 1. Reduce the system’s augmented matrix to (reduced) echelon form.
Step 2: Rewrite the echelon form matrix as a system of equations.
Step 3: Solve the equations as follows:
6a)
X + Y + 2Z = 8
-X -2Y + 3Z = 1
3X – 7Y + 4Z = 10
1
-1
3
1
-2
-7
2
3
4
R2  R2 + R1
1
0
0
1
-1
-10
2
5
-2
R2  -R2
1
1
2
0
1
-5
8
1
10
R3 R3 -3R1
8
9
-14
8
-9
0
-10
-2
R3R3+10R2
1
1
2
0
1
-5
0
0
-52
-14
8
-9
-104
R3R3/-52
1
0
0
1
1
0
2
-5
1
8
-9
2
THIS IS IN ECHELON FORM
SOLUTION BY GAUSSIAN ELIMINATION
X + Y +2Z = 8
Y – 5Z= -9
Z =2
SOLUTION
Z =2
Y = -9 + 5Z = 1
X = 8 – Y -2Z = 8 -1 -2(2) = 3
CONTINUE TO REDUCED ECHELON FORM
1
1
2
8
0
1
-5
-9
0
0
1
2
THIS IS IN ECHELON FORM
R1R1-R2
1
0
7
17
0
1
-5
-9
0
0
1
2
R2R2+5R3 R1R1 - 7R3
1
0
0
3
0
1
0
1
0
0
1
2
REDUCED ECHELON FORM
X
=3
Y
=1
Z =2
-----------------------------------------------------------
Example: suppose reduced echelon form of the augmented matrix is
1
0
2
0
0
1
0
2
X + 2Y
Z + 2W
5
3
Solve the system
= 5
=3
W=r
Z = 3 – 2W = 3 – 2r
Y= s
X = 5 – 2Y = 5 – 2s
Definition: A linear system is homogeneous provided all constants to the right of the
equals signs are 0
X + 2Y
Z + 2W
= 0
=0
A homogeneous system has one or many solutions.
Trivial solution: set all unknowns to zero.
A homogeneous system with 2 equations and 4 unknowns has many solutions with at
least 2 arbitrary variables.
The original system has n = 4 unknowns and m = 2 equations.
Reduce it to echelon form system, with r equations with r =2 or 1
If r = 2, the number of arbitrary variables is n –r = 4 -2 = 2
If r = 1, the number of arbitrary variables is n – r = 4 – 1 = 3
X + 2y +0z
+w=0
Has solution
W=r
Z=s
Y=t
X = -2y-w = -2t – r