Download Recitation Notes Spring 16, 21-241: Matrices and Linear Transformations January 19, 2016

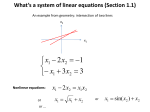
Recitation Notes
Spring 16, 21-241: Matrices and Linear Transformations
January 19, 2016
Abstract
[TOPICS COVERED] Row echelon form, Row reduced echelon form, Gauss-Jordan elimination, Logic and qualifiers, Negating statements.
1
Administrative Matters
• Course textbook: David Poole Linear Algebra: a modern introduction 4th edition.
CAUTION: Some exercises differ from the 3rd to the 4th edition. Be very careful
to check that you are doing the right problems if you want to use other editions.
• The homework assignment has problems from the textbook as well as from "Introduction to
mathematical arguments" by Michael Hutchings. Do not miss out anything.
• The problems from the pdf are Exercises 1 and 3 on page 12, NOT just Exercises 1(a) and
1(c).
• Use the pdf definitions for even and odd. Do NOT just use your intuitive understanding of
the terms.
• Introduction to mathematical arguments, right at the bottom of Exercise 1 it says:
What is the negation of each of these statements?
You need to do this too. Do NOT miss this out. Do NOT write an essay, use the symbols
Z, ∀, ∃, ∧, ∨, =⇒ , ⇐⇒.
2
Definitions
1. Row operations
2. Row echelon form
3. Reduced row echelon form (also known as Reduced echelon form. Keyword: Reduced)
4. Gauss-Jordan Elimination
5. Statement
6. Logic operators: ∧, ∨,
=⇒ , ⇔, ¬
7. Qualifiers: ∀, ∃
8. Even, odd
1
3
Problems
1. David Poole
following are

1 0
(a)  0 0
0 1

7 0
(b)  0 1
0 0
0 1
(c)
0 0

0 0

0 0
(d)
0 0

1 0

0 0
(e)
0 1

0 0

0 1
(f)
1 0

1 2
 1 0
(g) 
 0 1
0 0

2 1
 0 0
(h) 
 0 0
0 0
Linear Algebra: a modern introduction (4th Ed.) Ex 2.2.1-8. Which of the
in row echelon form?

1
3 
0

1 0
−1 4 
0 0
3 0
0 1

0
0 
0

3 −4 0
0 0 0 
5 0 1

1
0 
0

3
0 

1 
1

3 5
1 −1 

0 3 
0 0
Solution.
(a) No
(b) Yes, No
(c) Yes, Yes
(d) Yes, Yes
(e) No
(f) No
(g) No
(h) Yes, No
Page 2
2. David Poole Linear Algebra: a modern introduction (4th Ed.) Ex 2.1.28,30. Express the
following systems of linear equations in augmented matrix form
(a)
x1 + x2 + x3 = 1
x1 + x3 = 0
−x1 + 2x2 − 2x3 = 0
(b)
a − 2b + d = 2
−a + b − c − 3d = 1
Solution.
(a) We have:
1x1 +1x2 +1x3 = 1
1x1 +0x2 +1x3 = 0
−1x1 +2x2 −2x3 = 0
This gives the augmented matrix:


1 1 1 1
 1 0 1 0 
−1 2 −2 0
(b) We have:
1a −2b +0c +1d = 2
−1a +1b −1c −3d = 1
This gives the augmented matrix:
1 −2 0
1 2
−1 1 −1 −3 1
3. David Poole Linear Algebra: a modern introduction (4th Ed.) Ex 2.1.36. Solve the system in
2(b).
Page 3
Solution.
1 −2 0
1 2
−1 1 −1 −3 1
1 2
−−−−−−−−→ 1 −2 0
r2 7→ r2 + r1
0 −1 −1 −2 3
−−−−−−→ 1 −2 0 1 2
r2 7→ −r2
0 1 1 2 −3
−−−−−−−−−→ 1 0 2 5 −4
r1 7→ r1 + 2r2
0 1 1 2 −3
Therefore we have (a, b, c, d) = (−4 − 2s − 5t, −3 − s − 2t, s, t), s, t ∈ R.
4. Solve 2(a) from the augmented matrix above using Gauss-Jordan Elimination.
Solution.

1 1 1 1
 1 0 1 0 
−1 2 −2 0


1
1
1
1
−−−−−−−−→ 
0 −1 0 −1 
r2 7→ r2 − r1
−1 2 −2 0


1
1 1
1
−−−−−−−−→ 
r3 7→ r3 + r1 0 −1 0 −1 
0 3 −1 1


1 1 1 1
−−−−−−→ 
r2 7→ −r2 0 1 0 1 
0 3 −1 1


1 1 1
1
−−−−−−−−−→ 
1 
r3 7→ r3 − 3r2 0 1 0
0 0 −1 −2


1 1 1 1
−−−−−−→ 
r3 7→ −r3 0 1 0 1 
0 0 1 2


1 1 0 −1
−−−−−−−−→ 
r1 7→ r1 − r3 0 1 0 1 
0 0 1 2


1 0 0 −2
−−−−−−−−→ 
r1 7→ r1 − r2 0 1 0 1 
0 0 1 2

Note. Gauss-Jordan Elimination may not necessarily be the fastest way to obtain the rref
of a matrix.
Page 4
5. David Poole Linear Algebra: a modern introduction (4th Ed.) Ex 2.2.40. For what values of
k, if any, will the system
kx + 2y = 3
2x − 4y = −6
have
(a) no solution,
(b) a unique solution, and
(c) infinitely many solutions?
Solution.
Step 1: Express in augmented matrix form.
3
k 2
2 −4 −6
Step 2: Express in reduced row echelon form.
k 2
3
2 −4 −6
2 −4 −6
−
−
−
−
−
→
r1 ↔ r2
k 2
3
−−−−−−→ 1
1 −2 −3
r1 7→ r1
k 2
3
2
−−−−−−−−−→ 1
−3
−2
r2 7→ r2 − kr1
0 2 + 2k 3 + 3k
1
−2
−3
−→
0 2(1 + k) 3(1 + k)
Here we need to split into two cases.
Case 1: 1 + k = 0. Then we have
1
−2
1 −2 −3
−3
=
0 2(1 + k) 3(1 + k)
0 0
0
This gives us the solution (x, y) = (2t − 3, t) for t ∈ R.
Case 2: 1 + k 6= 0.
1
−2
−3
0 2(1 + k) 3(1 + k)
−−−−−−−−−→ 1
1 −2 −3
r2 7→
r2
0 2
3
1+k
−−−−−−−−→ 1 0 0
r1 7→ r1 + r2
0 2 3
−−−−−−→ 1
1 0 0
r2 7→ r2
0 1 32
2
Page 5
Thus there is unique solution (x, y) = (0, 23 ).
Step 3: Conclude.
(a) k ∈ ∅
(b) k 6= −1
(c) k = −1
6. Negate the following:
∃x P (x). ∀y Q(y). ∀z R(x, y, z)
Solution.
!
¬ ∃x P (x). ∀y Q(y). ∀z R(x, y, z)
−→ ∀x P (x). ¬ ∀y Q(y). ∀z R(x, y, z)
−→ ∀x P (x). ∃y Q(y). ¬ ∀z R(x, y, z)
−→ ∀x P (x). ∃y Q(y). ∃z ¬ R(x, y, z)
−→ ∀x P (x). ∃y Q(y). ∃z ¬R(x, y, z)
7. Prove the following statement:
For every integer x, if x is odd, then x2 is odd.
What is the negation of the statement?
Solution.
x is odd =⇒ ∃k ∈ Z. x = 2k + 1
=⇒ x2 = (2k + 1)2
=⇒ x2 = 4k 2 + 4k + 1
=⇒ x2 = 2(2k 2 + 2k) + 1
Since k ∈ Z, ` := 2k 2 + 2k ∈ Z. Thus ∃` ∈ Z. x2 = 2` + 1. Therefore x2 is odd.
Note: Notice how we conclude ’odd’ by definition. Notice also how we justified why ` is
an integer.
Page 6
4
Additional Notes
1. In definitions, we often just write "if", but what we mean is actually "if and only if". Do not
confuse this with implication statements.
2. Gauss-Jordan Elimination
Step 1: Swap zero-rows to the bottom
Step 2: Swap any row with left-most non-zero column to the top (if necessary)
Step 3: Perform scalar multiplication to make leading entry 1
Step 4: Subtract multiple of top row to other rows such that entries under the left-most non-zero
column are 0
Step 5: Repeat for remaining rows
Gauss-Jordan Elimination may not be the fastest way to obtain a solution when doing manual
computation. However, it is an algorithm, and is useful for programming a linear equations
solver.
3. Logic operators
¬
F
T
A
T
F
A
T
T
F
F
B
T
F
T
F
∧
T
F
F
F
∨
T
T
T
F
=⇒
T
F
T
T
⇐⇒
T
F
F
T
4. ¬(A =⇒ B) is equivalent to A ∧ ¬B
5. Familiarize with De Morgan’s Law, and distributivity and associativity of ∧ and ∨.
6. You cannot always commute qualifiers.
For example,
∃x ∈ R+ . ∀y ∈ R+ . y > x
is saying that "there exists a positive real number x such that all positive real numbers are
greater than x". This is clearly untrue (x is not greater than x).
∀y ∈ R+ . ∃x ∈ R+ . y > x
is saying that "for all positive real numbers, there is a positive real number that is less than
it". This is true, since for any y ∈ R+, y2 is also a positive real number and it is less than y.
Page 7