* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 2 - Ohio University
Voltage optimisation wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Electrical substation wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Buck converter wikipedia , lookup
Stray voltage wikipedia , lookup
Current source wikipedia , lookup
Alternating current wikipedia , lookup
Mains electricity wikipedia , lookup
Opto-isolator wikipedia , lookup
Two-port network wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
EE 616
Computer Aided Analysis of Electronic Networks
Lecture 2
Instructor: Dr. J. A. Starzyk, Professor
School of EECS
Ohio University
Athens, OH, 45701
1
EE 616
Review and Outline
2
Review of the previous lecture
-- Class organization
-- CAD overview
Outline of this lecture
* Review of network scaling
* Review of Thevenin/Norton Analysis
* Formulation of Circuit Equations
-- KCL, KVL, branch equations
-- Sparse Tableau Analysis (STA)
-- Nodal analysis
-- Modified nodal analysis
EE 616
Network scaling
3
EE 616
Network scaling (cont’d)
4
EE 616
Network scaling (cont’d)
5
EE 616
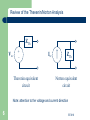
Review of the Thevenin/Norton Analysis
ZTh
Voc
+
–
Thevenin equivalent
circuit
Isc
ZTh
Norton equivalent
circuit
Note: attention to the voltage and current direction
6
EE 616
Review of the Thevenin/Norton Analysis
1. Pick a good breaking point in the circuit (cannot split a dependent
source and its control variable).
2.Replace the load by either an open circuit and calculate the voltage E
across the terminals A-A’, or a short circuit A-A’ and calculate the
current J flowing into the short circuit. E will be the value of the
source of the Thevenin equivalent and J that of the Norton
equivalent.
3. To obtain the equivalent source resistance, short-circuit all
independent voltage sources and open-circuit all independent current
sources. Transducers in the network are left unchanged. Apply a unit
voltage source (or a unit current source) at the terminals A-A’ and
calculate the current I supplied by the voltage source (voltage V
across the current source). The Rs = 1/I (Rs = V).
7
EE 616
Modeling
8
EE 616
Formulation of circuit equations (cont’d)
9
EE 616
Ideal two-terminal elements
10
EE 616
Ideal two-terminal elements
Topological equations
11
EE 616
KVL and KCL
Determined by the topology of the circuit
Kirchhoff’s Current Law (KCL): The algebraic
sum of all the currents leaving any circuit node is zero.
Kirchhoff’s Voltage Law (KVL): Every circuit
node has a unique voltage with respect to the reference node.
The voltage across a branch eb is equal to the difference
between the positive and negative referenced voltages of the
nodes on which it is incident
12
EE 616
Formulation of circuit equations (cont’d)
Unknowns
–
–
–
(i)
(e)
(v)
Equations
–
–
–
13
B branch currents
N node voltages
B branch voltages
KCL: N equations
KVL: B equations
Branch equations: B equations
EE 616
Branch equations
Determined by the mathematical model of the
electrical behavior of a component
–
14
Example: V=R·I
In most of circuit simulators this mathematical
model is expressed in terms of ideal elements
EE 616
Matrix form of KVL and KCL
B equations
N equations
15
EE 616
Branch equation
1
R
1
0
0
0
0
16
0
0
0
0 G2
1
0
R3
0
0
0
0
0
0
Kvv + i = is
1
R4
0
0
v
i
0
1 1
0 v
i2 0
2
0 v3 i3 0
v4 i4 0
0 v i i
5 5 s5
0
B equations
EE 616
Node branch incidence matrix
branches
1 2 3
n
o 1
d 2
e
s i
j
B
(+1, -1, 0)
N
{
Aij =
17
+1 if node i is terminal + of branch j
-1 if node i is terminal - of branch j
0 if node i is not connected to branch j
PROPERTIES
•A is unimodular
•2 nonzero entries in
each column
EE 616
Equation Assembly for Linear Circuits
–
Sparse Table Analysis (STA)
–
Modified Nodal Analysis (MNA)
18
Brayton, Gustavson, Hachtel
McCalla, Nagel, Roher, Ruehli, Ho
EE 616
Sparse Tableau Analysis (STA)
19
EE 616
Advantages and problems of STA
20
EE 616
Nodal analysis
1.
2.
3.
Write KCL
A·i=0
(N equations, B unknowns)
Use branch equations to relate branch currents to
branch voltages
i=Yv
(B equations, B unknowns)
Use KVL to relate branch voltages to node
voltages
v=ATe
(B equations, N unknowns)
Yne=ins
21
Nodal Matrix
N equations
N unknowns
N = # nodes
EE 616
Nodal analysis
22
EE 616
Nodal analysis – Resistor “Stamp”
Spice input format: Rk
N+
N+
Rk
N-
i
1
N+
R
k
1
Rk
N-
Rkvalue
N1
Rk
1
Rk
1
iothers R eN eN is
k
KCL at node N+
1
eN eN is
Rk
KCL at node N-
iothers
23
N+ N-
EE 616
Nodal analysis – VCCS “Stamp”
Spice input format: Gk
NC+
NC-
-
i
i
others
others
24
N+
+
vc
N+ N- NC+ NC-
Gkvalue
NC+
N+ G
k
G
k
N-
Gkvc
NC-
Gk
Gk
N-
Gk eNC eNC is
Gk eNC eNC is
KCL at node N+
KCL at node NEE 616
Nodal analysis- independent current sources “stamp”
25
EE 616
Nodal analysis- by inspection
Rules (page 36):
1.
The diagonal entries of Y are positive and
y jj admittances connected to node j
2. The off-diagonal entries of Y are negative and are given by
y jk admittances connected between nodes j and k
3. The jth entry of the right-hand-side vector J is
J j currents from independent sources entering node j
26
EE 616
Example of nodal analysis by inspection
Exercise
Formulate nodal equations by inspection
27
EE 616
Example of nodal analysis by inspection
28
EE 616
Example of nodal analysis by inspection
Exercise
Formulate nodal equations by inspection
29
EE 616
Example of nodal analysis by inspection
Exercise
30
EE 616
Nodal analysis (cont’d)
31
EE 616
Modified Nodal Analysis (MNA)
32
EE 616
Modified Nodal Analysis (2)
33
1
1
G2
R3
R1
1
R3
0
0
0
E7
1
G2
R3
1
1
R3 R4
0
0
0
0
1
1
R8
1
R8
1
E7
0
0
0
1
R8
1
R8
0
1
0
e 0
1
1 0 e i
2 s5
e 0
3
1 0
e4 0
0 1 i6 ES 6
i7 0
0 0
0 0
0
EE 616
Modified Nodal Analysis (3)
34
EE 616
General rules for MNA
35
EE 616
Example 4.4.1(p.143)
36
EE 616
Advantages and problems of MNA
37
EE 616
Analysis of networks with VVT’s & Op Amps
38
EE 616
Example 4.5.2 (p.145)
39
EE 616
Example 4.5.5 (p. 148)
40
EE 616
Example 4.5.5 (cont’d)
41
EE 616