* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Review of aggregate production function
Survey
Document related concepts
Fear of floating wikipedia , lookup
Business cycle wikipedia , lookup
Steady-state economy wikipedia , lookup
Ragnar Nurkse's balanced growth theory wikipedia , lookup
Fei–Ranis model of economic growth wikipedia , lookup
Okishio's theorem wikipedia , lookup
Transcript
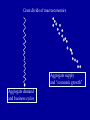
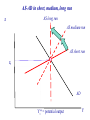
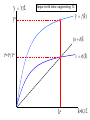
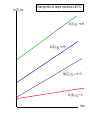
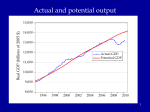
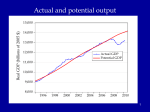
The first known anthro-capital Olduvai stone chopping tool, 1.8 – 2 million years BP 1 Report from the Fed • Hello to Econ 122 from Vice-chair Yellen • Report from former Yale TA William Nelson to the Chairs of the Regional Federal Reserves … on forward guidance • Valediction for Chairman Bernanke “character, integrity, competence” 2 Agenda • • • • • • Introductory background Essential aspects of economic growth Aggregate production functions Neoclassical growth model Simulation of increased saving experiment Then in the last week: deficits, debt, and economic growth 3 Great divide of macroeconomics Aggregate supply and “economic growth” Aggregate demand and business cycles Actual and potential output Economic growth: Studies growth of potential output Congressional Budget Office, March 2013, cbo.gov. 5 Potential and actual real output in the long run 20,000 16,000 14,000 12,000 Potential output Actual output 10,000 8,000 6,000 4,000 2,000 1950 1960 1970 1980 1990 2000 2010 6 How do they fit together? Examples of why Keynesian Classical In long run, prices and wages are flexible. In long run, expectations are accurate (rational?). In long run, entry and exit make economy more competitive. All these make long-run look more classical than short run. 7 AS-AD in short, medium, long run AS long run π AS medium run AS short run πt AD Yt* = potential output Y Growth trend, US, 1948-2008 (pre-recession) 2.0 ln(K) ln(Y) ln(hours) 1.6 1.2 0.8 0.4 0.0 50 55 60 65 70 75 80 85 90 95 00 05 9 Historical Trends in Economic Growth in the US since 1800 1. Strong growth in Y 2. Strong growth in productivity (both Y/L and TFP, total factor productivity) 3. Steady “capital deepening” (increase in K/L) 4. Strong growth in real wages since early 19th C; g(w/p) ~ g(X/L) 5. Real interest rate and profit rate basically trendless 10 Capital deepening in agriculture Food for Commons Morocco, 2002 11 Mining in rich and poor countries D.R. Congo Canada 12 Review of aggregate production function Yt = At F(Kt, Lt) Kt = capital services (like rentals as apartment-years) Lt = labor services (hours worked) At = level of technology gx = growth rate of x = (1/xt) dxt/dt = Δ xt/xt-1 = d[ln(xt))]/dt gA = growth of technology = rate of technological change = Δ At/At-1 Constant returns to scale: λYt = At F(λKt, λLt), or all inputs increased by λ means output increased by λ Perfect competition in factor and product markets (for p = 1): MPK = ∂Y/∂K = R = rental price of capital; ∂Y/∂L = w = wage rate Exhaustion of product with CRTS: MPK x K + MPL x L = RK + wL = Y Alternative measures of productivity: Labor productivity = Yt/Lt Total factor productivity (TFP) = At = Yt /F(Kt, Lt) 13 Review: Cobb-Douglas aggregate production function Remember Cobb-Douglas production function: or Yt = At Kt α Lt 1-α ln(Yt)= ln(At) + α ln(Kt) +(1-α) ln(Lt) Here α = ∂ln(Yt)/∂ln(Kt) = elasticity of output w.r.t. capital; (1-α ) = elasticity of output w.r.t. labor MPK = Rt = α At Kt α-1 Lt 1-α = α Yt/Kt Share of capital in national income = Rt Kt /Yt = α = constant. Ditto for share of labor. 14 The MIT School of Economics Robert Solow (1924 - ) Paul Samuelson (1915-2009) 15 Basic neoclassical growth model Major assumptions: 1. Basic setup: - full employment - flexible wages and prices - perfect competition - closed economy 2. Capital accumulation: ΔK = sY – δK; s = investment rate = constant 3. Labor supply: Δ L/L = n = exogenous 4. Production function - constant returns to scale - two factors (K, L) - single output used for both C and I: Y = C + I - no technological change to begin with - in next model, labor-augmenting technological change 5. Change of variable to transform to one-equation model: k = K/L = capital-labor ratio Y = F(K, L) = LF(K/L,1) y = Y/L = F(K/L,1) = f(k), where f(k) is per capita production fn. 16 Major variables: Y = output (GDP) L = labor inputs K = capital stock or services I = gross investment w = real wage rate r = real rate of return on capital (rate of profit) E = efficiency units = level of labor-augmenting technology (growth of E is technological change = ΔE/E) ~ ~ L = efficiency labor inputs = EL = similarly for other variables with “ ”notation) Further notational conventions Δ x = dx/dt gx = growth rate of x = (1/x) dx/dt = Δxt/xt-1=dln(xt)/dt s = I/Y = savings and investment rate k = capital-labor ratio = K/L c = consumption per capita = C/L i = investment per worker = I/L δ = depreciation rate on capital y = output per worker = Y/L n = rate of growth of population (or labor force) = gL = Δ L/L v = capital-output ratio = K/Y h = rate of labor-augmenting technological change 17 We want to derive “laws of motion” of the economy. To do this, start with (math on next slide): 5. Δ k/k = Δ K/K - Δ L/L With some algebra,* this becomes: 5’. Δ k/k = Δ K/K - n Y, or Δ k = sf(k) - (n + δ) k which in steady state is: 6. sf(k*) = (n + δ) k* In steady state, y, k, w, and r are constant. No growth in real wages, real incomes, per capita output, etc. *The algebra of the derivation: ΔK/K = (sY – δK)/K = s(Y/L)(L/K) – δ Δk/k = ΔK/K – n = s(Y/L)(L/K) – δ – n Δk = k [ s(Y/L)(L/K) – δ – n] = sy – (δ + n)k = sf(k) – (δ + n)k 18 Mathematical note We will use the following math fact: Define z = y/x Then (1) (Growth rate of z) = (growth rate of y) – (growth rate of x) Or gz = gy - gx Proof: Using logs: ln(zt) = ln(yt )– ln(xt) Taking time derivative: [dzt/dt]/zt = [dyt/dt]/yt - [dxt/dt]/xt which is the desired result. Note that we sometimes use the discrete version of (1), as we did in the last slide. This has a small error that is in the order of the size of the time step or the growth rates. For example, if gy = 5 % and gx = 3 %, then by the formula gz = 2 %, while the exact calculation is that gz = 1.9417 %. This is close enough for expository purposes. 19 y = Y/L y* y = f(k) (n+δ)k i = sf(k) i* = (I/Y)* k* k 20 Results of neoclassical model without TC y = Y/L Predictions of basic model: – “Steady state” – constant y, w, k, and r – gY = n Uniqueness and stability of equilibrium. – Equilibrium is unique – Equilibrium is stable (meaning k → k* as t → ∞ for all initial k0). y* y = f(k) (n+δ)k i = sf(k) i* = (I/Y)* k* k 26 21 But does it match the growth trends from the historical record? No. What is missing from the NCM up to now? Technological change! 22 Economic growth (II): Technological change 23 World fastest supercomputer, 2012 (Tianhe-2 in NUDT, Guangzhou, China ) at 33.8 petaflops (34x1015 floating point operations per second , up from 16.2 last year) Economic Growth (II): Technological Change Yale Abacus master (.03 flops) IBM 1620, circa 1960 (104 flops) High-end PC, 2013 (1011 flops) Tianhe-2, top supercomputer, 2013 (34x1015 flops) [flop = floating point operations per second, e.g., 1011011011001001+0010110100010101] Review from last time Neoclassical growth model is classical model + time Major dynamic equation: Δ kt = sf(kt) - (n + δ) kt Without technological change (TC): - Long-run growth is gY = gK = n; gw = gk = gy = 0 - Change in n, s affect level, not growth in the long run NCM without TC cannot explain basic trends. So now introduce TC. 25 Introducing technological change First model omits technological change (TC). What is TC? • New processes that increase TFP (assembly line, fiber optics) • Improvements in quality of goods (plasma TV) • New goods and services (automobile, telephone, Twitter) Analytically, TC is - Shift in production function. y = Y/L new f(k) old f(k) k* k 26 The Wealth of Nations Why do countries, regions, people have such divergent incomes? • People in US: top 1% to bottom 1 %: 717,000/$1000? • US states: top county to bottom county: $132,700/$5213 (Wyoming/South Dakota) • Top to bottom country: $88,900/$375 (Qatar/Congo) Most of the differences among regions are technological, so need to understand the economics of technological change. 27 Technological change in medicine Scan for lung cancer African medicine man 28 Disappearance of polio: A benefit of growth that is not captured in the GDP statistics! Introducing technological change We take specific form which is “labor-augmenting technological change” at rate h. For this, we need new variable called “efficiency labor units” denoted as E ~ where E = efficiency units of labor and indicates efficiency units. L=EL New production function is then y = Y/L new f(k) Y F K , EL F(K , L ) old f(k) F K , L L F K/L , 1 L f ( k ), where k K / L y k* k Y / L f (k) Note: Redefining labor units in efficiency terms is a specific way of representing TC that makes everything work out easily. Other forms of TC will give slightly different results. 30 The math with technological change is this: y Y / L f (k ) k = K /L k = s f (k ) (n h ) k Test the long-run equilibrium of k 0 : s f ( k ) = (n h ) k In Cobb-Douglas case: Set A0 E 0 1 for simplicity without loss of generality. Y t K t ( e ht Lt )1 y t Y t / L t K t ( e ht Lt )1 / L t Kt L t1 / L t y t Kt L t = k t 31 Results of neoclassical model with labor-augmenting TC For C-D case, sk * ( n h )k * k * s /( n h ) 1/(1 ) y * s /( n h ) /(1 ) Unique and stable equilibrium under standard assumptions: Predictions of basic model: – Steady state: constant y, w, k, and r ; these all grow at h. – Labor’s share of output is constant. – Hence, captures the basic trends! 32 y Y/L Impact with labor-augmenting TC y f ( k) y* (n )k i*=I*/Y* i sf ( k ) k* 33 k=K/L ln (Y), etc. Time profiles of major variables with TC ln (Y); gY = n+h ln (K); gK = n+h ln( L); gL n h ln (L) ); gL = n time 34 What are the contributors to growth? Growth Accounting Growth accounting is a widely used technique used to separate out the sources of growth in a country; it relies on the neoclassical growth model Assume Cobb-Douglas, and calculate growth rates: Take logarithms and time derivative: g(Yt) = g(At )+ α g(Kt) + (1 - α) g(Lt ) Or if we assume competitive α = sh(K) and (1- α) = sh(L) g(Y) = g(A) + sh(K) g(K) + sh(L) g(L ) Subtract growth of labor to get per capita growth: g(Y)- g(L ) = g(y ) = g(A) + sh(K) g(k) 35 Per capita output g(y) = g(A) + sh(K) (g(k)) g(A) = g(y) - sh(K) (g(k)) Historical data: g(y) = 1.7% p.y.; sh(K) = ¼; g(k) = 2.4% p.y. g(A) = 1.7 % – 0.25 2.4% = 1.1% So contribution to p.c. y growth is Of A: 1.1%, or 65% of total Of k: ¼ x 2.4, or 35% of total This is the very surprising results that technology contributes most of the rise in per capita output over the period. Similar in other countries/periods. Source: BLS, multifactor productivity page. 36 Understanding Technological Change TC is conceptually much more difficult than investment: - TC depends upon invention and innovation - Market failure: big gap between social MP and private MP of inventive activity - No formula for discovery analogous to increased saving. Major instruments: - Intellectual property rights (create monopoly to reduce MP gap): patents, copyrights - Government subsidy of research (direct to Yale; indirect through R&D tax credit) - Rivalry but not perfect competition in markets (between Windows and Farmer Jones) - Openness to foreign technologies and management practices 37 Several “comparative dynamics” experiments • Change growth in labor force (immigration or retirement policy) • Change in rate of TC • Change in national savings and investment rate (tax changes, savings changes, demographic changes) Here we will investigate only a change in the national savings rate. 38 Jobs today … or … consumption tomorrow? Two faces of saving 39 National savings and fiscal policy The major long-run policy to affect national savings is fiscal policy. Remember: S = Sp + Sg = Sp + T – G We show the analysis today, and return to the controversies of fiscal policy at the end of the course. 40 y** Impact of Higher National Saving y = f(k) y* i = s2f(k) i = s1f(k) (I/Y)* (n+δ)k k k* k** 41 Numerical Example of Deficit Reduction Assumptions: 1. Production is by Cobb-Douglas with CRTS 2. Labor plus labor-augmenting TC: 1. n = 1.5 % p.a.; h = 1.5 % p.a. 3. Full employment; constant labor force participation rate. 4. Savings assumption: a. Private savings rate = 22% of GDP b. Initial govt. savings rate = minus 6 % of GDP c. In 2012, govt. changes fiscal policy to a deficit of minus 2 % of GDP. d. All of higher govt. S goes into national S (i.e., constant private savings rate) and closed economy 5. “Calibrate” to U.S. economy 42 Impact of Lower Govt Deficit on Major Variables 2010 2015 2020 2025 2030 35% Consumption per capita Percent change from baseline 30% GDP per capita Capital per capita 25% 20% NNP per capita - Note that takes 10 years to increase C -Political implications - Must C increase? - No if k>kgoldenrule 15% 10% 5% 0% -5% -10% 43 Summary • Neoclassical model is workhorse of long-run growth theory. • NCM + TC does good job of explaining major trends. • Make sure you understand the impacts of changing n, s, and h. • Changes in fiscal policy affect mainly national savings. • Innovation policy is a critical and poorly understood aspect of economic policy. 44