Download Review of aggregate production function

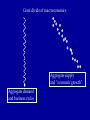
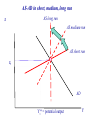
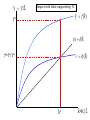
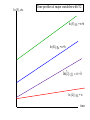
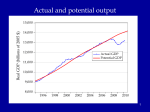
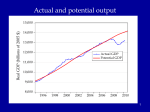
The first known anthro-capital
Olduvai stone chopping tool, 1.8 – 2 million years BP
1
Report from the Fed
• Hello to Econ 122 from Vice-chair Yellen
• Report from former Yale TA William Nelson to the
Chairs of the Regional Federal Reserves
… on forward guidance
• Valediction for Chairman Bernanke
“character, integrity, competence”
2
Agenda
•
•
•
•
•
•
Introductory background
Essential aspects of economic growth
Aggregate production functions
Neoclassical growth model
Simulation of increased saving experiment
Then in the last week: deficits, debt, and economic
growth
3
Great divide of macroeconomics
Aggregate supply
and “economic growth”
Aggregate demand
and business cycles
Actual and potential output
Economic growth:
Studies growth of
potential output
Congressional Budget Office, March 2013, cbo.gov.
5
Potential and actual real output in the long run
20,000
16,000
14,000
12,000
Potential output
Actual output
10,000
8,000
6,000
4,000
2,000
1950
1960
1970
1980
1990
2000
2010
6
How do they fit together?
Examples of why Keynesian  Classical
In long run, prices and wages are flexible.
In long run, expectations are accurate (rational?).
In long run, entry and exit make economy more competitive.
All these make long-run look more classical than short run.
7
AS-AD in short, medium, long run
AS long run
π
AS medium run
AS short run
πt
AD
Yt* = potential output
Y
Growth trend, US, 1948-2008 (pre-recession)
2.0
ln(K)
ln(Y)
ln(hours)
1.6
1.2
0.8
0.4
0.0
50
55
60
65
70
75
80
85
90
95
00
05
9
Historical Trends in Economic Growth
in the US since 1800
1. Strong growth in Y
2. Strong growth in productivity (both Y/L and TFP, total factor
productivity)
3. Steady “capital deepening” (increase in K/L)
4. Strong growth in real wages since early 19th C; g(w/p) ~ g(X/L)
5. Real interest rate and profit rate basically trendless
10
Capital deepening in agriculture
Food for Commons
Morocco, 2002
11
Mining in rich and poor countries
D.R. Congo
Canada
12
Review of aggregate production function
Yt = At F(Kt, Lt)
Kt = capital services (like rentals as apartment-years)
Lt = labor services (hours worked)
At = level of technology
gx = growth rate of x = (1/xt) dxt/dt = Δ xt/xt-1 = d[ln(xt))]/dt
gA = growth of technology = rate of technological change = Δ At/At-1
Constant returns to scale: λYt = At F(λKt, λLt), or all inputs increased by λ
means output increased by λ
Perfect competition in factor and product markets (for p = 1):
MPK = ∂Y/∂K = R = rental price of capital; ∂Y/∂L = w = wage rate
Exhaustion of product with CRTS:
MPK x K + MPL x L = RK + wL = Y
Alternative measures of productivity:
Labor productivity = Yt/Lt
Total factor productivity (TFP) = At = Yt /F(Kt, Lt)
13
Review: Cobb-Douglas aggregate production function
Remember Cobb-Douglas production function:
or
Yt = At Kt α Lt 1-α
ln(Yt)= ln(At) + α ln(Kt) +(1-α) ln(Lt)
Here α = ∂ln(Yt)/∂ln(Kt) = elasticity of output w.r.t. capital;
(1-α ) = elasticity of output w.r.t. labor
MPK = Rt = α At Kt α-1 Lt 1-α = α Yt/Kt
Share of capital in national income = Rt Kt /Yt = α = constant. Ditto
for share of labor.
14
The MIT School of Economics
Robert Solow (1924 - )
Paul Samuelson (1915-2009)
15
Basic neoclassical growth model
Major assumptions:
1. Basic setup:
- full employment
- flexible wages and prices
- perfect competition
- closed economy
2. Capital accumulation: ΔK = sY – δK; s = investment rate = constant
3. Labor supply: Δ L/L = n = exogenous
4. Production function
- constant returns to scale
- two factors (K, L)
- single output used for both C and I: Y = C + I
- no technological change to begin with
- in next model, labor-augmenting technological change
5. Change of variable to transform to one-equation model:
k = K/L = capital-labor ratio
Y = F(K, L) = LF(K/L,1)
y = Y/L = F(K/L,1) = f(k), where f(k) is per capita production fn.
16
Major variables:
Y = output (GDP)
L = labor inputs
K = capital stock or services
I = gross investment
w = real wage rate
r = real rate of return on capital (rate of profit)
E = efficiency units = level of labor-augmenting technology (growth of E is technological
change = ΔE/E)
~
~
L = efficiency labor inputs = EL = similarly for other variables with “ ”notation)
Further notational conventions
Δ x = dx/dt
gx = growth rate of x = (1/x) dx/dt = Δxt/xt-1=dln(xt)/dt
s = I/Y = savings and investment rate
k = capital-labor ratio = K/L
c = consumption per capita = C/L
i = investment per worker = I/L
δ = depreciation rate on capital
y = output per worker = Y/L
n = rate of growth of population (or labor force)
= gL = Δ L/L
v = capital-output ratio = K/Y
h = rate of labor-augmenting technological change
17
We want to derive “laws of motion” of the economy. To do this, start
with (math on next slide):
5. Δ k/k = Δ K/K - Δ L/L
With some algebra,* this becomes:
5’. Δ k/k = Δ K/K - n Y, or
Δ k = sf(k) - (n + δ) k
which in steady state is:
6. sf(k*) = (n + δ) k*
In steady state, y, k, w, and r are constant. No growth in real wages,
real incomes, per capita output, etc.
*The algebra of the derivation:
ΔK/K = (sY – δK)/K = s(Y/L)(L/K) – δ
Δk/k = ΔK/K – n = s(Y/L)(L/K) – δ – n
Δk = k [ s(Y/L)(L/K) – δ – n]
= sy – (δ + n)k = sf(k) – (δ + n)k
18
Mathematical note
We will use the following math fact:
Define z = y/x
Then
(1) (Growth rate of z) = (growth rate of y) – (growth rate of x)
Or gz = gy - gx
Proof:
Using logs:
ln(zt) = ln(yt )– ln(xt)
Taking time derivative:
[dzt/dt]/zt = [dyt/dt]/yt - [dxt/dt]/xt
which is the desired result.
Note that we sometimes use the discrete version of (1), as we did in the
last slide. This has a small error that is in the order of the size of the
time step or the growth rates. For example, if gy = 5 % and gx = 3 %,
then by the formula gz = 2 %, while the exact calculation is that gz =
1.9417 %. This is close enough for expository purposes.
19
y = Y/L
y*
y = f(k)
(n+δ)k
i = sf(k)
i* =
(I/Y)*
k*
k
20
Results of neoclassical model without TC
y = Y/L
Predictions of basic model:
– “Steady state”
– constant y, w, k, and r
– gY = n
Uniqueness and stability of
equilibrium.
– Equilibrium is unique
– Equilibrium is stable
(meaning k → k*
as t → ∞ for all initial k0).
y*
y = f(k)
(n+δ)k
i = sf(k)
i* =
(I/Y)*
k*
k
26
21
But does it match the growth trends from the historical
record?
No.
What is missing from the NCM up to now?
Technological change!
22
Economic growth (II): Technological change
23
World fastest supercomputer, 2012 (Tianhe-2 in NUDT, Guangzhou, China ) at 33.8
petaflops (34x1015 floating point operations per second , up from 16.2 last year)
Economic Growth (II): Technological Change
Yale
Abacus master
(.03 flops)
IBM 1620, circa 1960
(104 flops)
High-end PC, 2013
(1011 flops)
Tianhe-2, top supercomputer, 2013
(34x1015 flops)
[flop = floating point operations per second, e.g., 1011011011001001+0010110100010101]
Review from last time
Neoclassical growth model is classical model + time
Major dynamic equation:
Δ kt = sf(kt) - (n + δ) kt
Without technological change (TC):
- Long-run growth is gY = gK = n; gw = gk = gy = 0
- Change in n, s affect level, not growth in the long run
NCM without TC cannot explain basic trends.
So now introduce TC.
25
Introducing technological change
First model omits technological change (TC).
What is TC?
• New processes that increase TFP (assembly line, fiber
optics)
• Improvements in quality of goods (plasma TV)
• New goods and services (automobile, telephone, Twitter)
Analytically, TC is
- Shift in production function.
y = Y/L
new f(k)
old f(k)
k*
k
26
The Wealth of Nations
Why do countries, regions, people have such divergent
incomes?
• People in US: top 1% to bottom 1 %: 717,000/$1000?
• US states: top county to bottom county: $132,700/$5213
(Wyoming/South Dakota)
• Top to bottom country: $88,900/$375 (Qatar/Congo)
Most of the differences among regions are technological, so
need to understand the economics of technological change.
27
Technological change in medicine
Scan for lung
cancer
African medicine man
28
Disappearance of polio:
A benefit of growth that is not captured
in the GDP statistics!
Introducing technological change
We take specific form which is “labor-augmenting technological
change” at rate h.
For this, we need new variable called “efficiency labor units”
denoted as E
~
where E = efficiency units of labor and indicates efficiency units.
L=EL
New production function is then
y = Y/L
new f(k)
Y  F  K , EL   F(K , L )
old f(k)
 F  K , L   L F  K/L , 1 
 L f ( k ), where k  K / L
y
k*
k
 Y / L  f (k)
Note: Redefining labor units in efficiency terms is a specific way of
representing TC that makes everything work out easily. Other
forms of TC will give slightly different results.
30
The math with technological change is this:
y
 Y / L  f (k )
k = K /L
 k = s f (k )  (n  h   ) k
Test the long-run equilibrium of  k  0 :
s f ( k ) = (n  h   ) k
In Cobb-Douglas case: Set A0  E 0  1 for simplicity
without loss of generality.
Y t  K t ( e ht Lt )1
y t  Y t / L t  K t ( e ht Lt )1 / L t  Kt L t1 / L t
y t  Kt L t = k t
31
Results of neoclassical model with labor-augmenting TC
For C-D case,
sk *  ( n  h   )k *
k *   s /( n  h   ) 1/(1 )
y *   s /( n  h   )  /(1 )
Unique and stable equilibrium under standard assumptions:
Predictions of basic model:
– Steady state: constant y, w, k, and r ; these all grow at h.
– Labor’s share of output is constant.
– Hence, captures the basic trends!
32
y  Y/L
Impact with labor-augmenting TC
y  f ( k)
y*
(n   )k
i*=I*/Y*
i  sf ( k )
k*
33
k=K/L
ln (Y), etc.
Time profiles of major variables with TC
ln (Y); gY = n+h
ln (K); gK = n+h
ln( L); gL  n  h
ln (L) ); gL = n
time
34
What are the contributors to growth? Growth Accounting
Growth accounting is a widely used technique used to separate
out the sources of growth in a country; it relies on the
neoclassical growth model
Assume Cobb-Douglas, and calculate growth rates:
Take logarithms and time derivative:
g(Yt) = g(At )+ α g(Kt) + (1 - α) g(Lt )
Or if we assume competitive α = sh(K) and (1- α) = sh(L)
g(Y) = g(A) + sh(K) g(K) + sh(L) g(L )
Subtract growth of labor to get per capita growth:
g(Y)- g(L ) = g(y ) = g(A) + sh(K) g(k)
35
Per capita output
g(y) = g(A) + sh(K) (g(k))
g(A) = g(y) - sh(K) (g(k))
Historical data:
g(y) = 1.7% p.y.; sh(K) = ¼; g(k) = 2.4% p.y.
g(A) = 1.7 % – 0.25 2.4% = 1.1%
So contribution to p.c. y growth is
Of A:
1.1%, or 65% of total
Of k:
¼ x 2.4, or 35% of total
This is the very surprising results that technology contributes most of the
rise in per capita output over the period. Similar in other
countries/periods.
Source: BLS, multifactor productivity page.
36
Understanding Technological Change
TC is conceptually much more difficult than investment:
- TC depends upon invention and innovation
- Market failure: big gap between social MP and private MP of
inventive activity
- No formula for discovery analogous to increased saving.
Major instruments:
- Intellectual property rights (create monopoly to reduce MP gap):
patents, copyrights
- Government subsidy of research (direct to Yale; indirect through
R&D tax credit)
- Rivalry but not perfect competition in markets (between Windows
and Farmer Jones)
- Openness to foreign technologies and management practices
37
Several “comparative dynamics” experiments
• Change growth in labor force (immigration or retirement
policy)
• Change in rate of TC
• Change in national savings and investment rate (tax changes,
savings changes, demographic changes)
Here we will investigate only a change in the national savings
rate.
38
Jobs today … or …
consumption tomorrow?
Two faces of saving
39
National savings and fiscal policy
The major long-run policy to affect national savings is fiscal
policy. Remember:
S = Sp + Sg = Sp + T – G
We show the analysis today, and return to the
controversies of fiscal policy at the end of the course.
40
y**
Impact of Higher National Saving
y = f(k)
y*
i = s2f(k)
i = s1f(k)
(I/Y)*
(n+δ)k
k
k*
k**
41
Numerical Example of Deficit Reduction
Assumptions:
1. Production is by Cobb-Douglas with CRTS
2. Labor plus labor-augmenting TC:
1.
n = 1.5 % p.a.; h = 1.5 % p.a.
3. Full employment; constant labor force participation rate.
4. Savings assumption:
a. Private savings rate = 22% of GDP
b. Initial govt. savings rate = minus 6 % of GDP
c. In 2012, govt. changes fiscal policy to a deficit of minus 2 %
of GDP.
d. All of higher govt. S goes into national S (i.e., constant
private savings rate) and closed economy
5.
“Calibrate” to U.S. economy
42
Impact of Lower Govt Deficit on Major Variables
2010
2015
2020
2025
2030
35%
Consumption per capita
Percent change from baseline
30%
GDP per capita
Capital per capita
25%
20%
NNP per capita
- Note that takes 10
years to increase C
-Political
implications
- Must C increase?
- No if k>kgoldenrule
15%
10%
5%
0%
-5%
-10%
43
Summary
• Neoclassical model is workhorse of long-run
growth theory.
• NCM + TC does good job of explaining major
trends.
• Make sure you understand the impacts of
changing n, s, and h.
• Changes in fiscal policy affect mainly national
savings.
• Innovation policy is a critical and poorly
understood aspect of economic policy.
44