* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Introduction to Planning
Survey
Document related concepts
Transcript
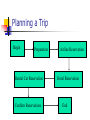
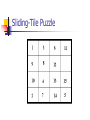
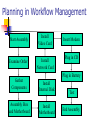
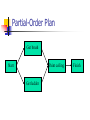
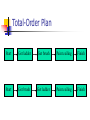
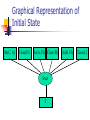
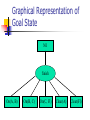
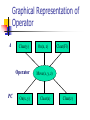
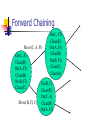
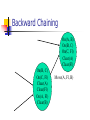
Introduction to Planning Han Yu University of Central Florida Outline What is planning? Formal definitions of planning problems Basic planning algorithms Recent development What is Planning? Planning is a search problem that requires to find an efficient sequence of actions that transform a system from a given starting state to the goal state What’s Given? Initial state of the problem Goal state of the problem A finite set of actions: pre-conditions: a finite set of conditions for the action to be performed post-conditions: a finite set of conditions that will be changed after the action is performed cost What’s Output? A sequence of actions that meet the following criteria every action matches the current system state can transform system from initial state to goal state the total cost of the actions is below a specified value Planning as a Real-World Problem Planning problem has a wide range of applications in the real world planning in daily life game world workflow management Planning a Trip Begin Preparation Rental Car Reservation Confirm Reservations Airline Reservation Hotel Reservation End Towers of Hanoi Problem Analysis Optimal solution contains 2n-1 actions, where n is the number of disks Up to 6 possible actions in each system state The upper bound on search space to n-1) (2 find an optimal solution will be 6 Sliding-Tile Puzzle Planning in Workflow Management Start Assembly Examine Order Gather Components Assembly Box and Motherboard Install Video Card Install Network Card Insert Modem Plug in CD Plug in Battery Install Internal Disk Install Motherboard Test End Assembly Partial-Order Plan versus Total-Order Plan Partial-order plan consists partially ordered set of actions sequence constraints exist on these actions plan generation algorithm can be applied to transform partial-order plan to total-order plan Total-order plan consists totally ordered set of actions Partial-Order Plan Get brush Paint ceiling Start Get ladder Finish Total-Order Plan Start Get ladder Get brush Paint ceiling Finish Start Get brush Get ladder Paint ceiling Finish Features of Planning Problems Large search space Action is associated with system states Restrictions on the action sequence Valid solution may not exist Optimization requirement STRIPS Planning System A tuple T = (P, O, I, G), where P is a finite set of ground literals, the conditions O is a finite set of operators I is the initial state, a subset of P G is the goal state, a subset of P STRIPS Operators Each operator O has the following attributes PC, a set of ground literals, defines the precondition of the operator D, a set of ground literals, defines the conditions that will be removed after the operation is executed A, a set of ground literals, defines the conditions that will be added after the operation is executed C, the cost of the operation A Simple Example - Blocks World A C A B B Initial State On(C, A) Clear(Fl) On(A, Fl) Clear(B) On(B, Fl) Clear(C) C Goal State On(A, B) On(B, C) On(C, Fl) Clear(A) Clear(Fl) Graphical Representation of Initial State On(C, A) Clear(Fl) On(A, Fl) Clear(B) Start T On(B, Fl) Clear(C) Graphical Representation of Goal State Nil finish On(A, B) On(B, C) On(C, Fl) Clear(A) Clear(Fl) Block World - Operator Move(x, y, z) Move block x that is above y to above z PC: On(x,y), Clear(x), Clear(z) D: Clear(z), On(x, y) A: On(x,z), Clear(y), Clear(Fl) Graphical Representation of Operator A Clear(y) Operator PC On(x, y) On(x, z) Clear(Fl) Move(x, y, z) Clear(x) Clear(z) Forward Chaining Search from the initial state Expand the search tree by finding the set of all applicable operators from the current state applicable means the precondition of the operator is a subset of current state Update current state For every state that is reached, record the shortest path (or path with lowest cost) from the initial state to this state If the goal state is reached, stop the algorithm Forward Chaining On(C, Fl) Clear(Fl) On(A, Fl) Clear(B) On(B, Fl) Clear(C) Clear(A) Move(C, A, Fl) On(C, A) Clear(Fl) On(A, Fl) Clear(B) On(B, Fl) On(B, C) Clear(C) Clear(Fl) Move(B, Fl, C) On(C, A) Clear(B) On(A, Fl) Backward Chaining Search backward from the goal state Expand the search tree by finding the set of all applicable operators that can reach the current state applicable means set A of the operator is a subset of current state Update the state If the initial state is reached, stop the algorithm The solution is a partial-ordered plan Constraints in action ordering may be violated Backward Chaining On(A, B) On(B, C) On(C, Fl) Clear(A) Clear(Fl) On(B, C) On(C, Fl) Clear(A) Clear(Fl) On(A, Fl) Clear(B) Move(A, Fl, B) Recent Developments Plan Reuse Graphplan Problem-specific planning Evolutionary computation approach Plan Reuse Reuse old plans for new planning problems Consists of two steps plan matching plan modification Research findings generally, plan reuse is even harder than plan from scratch do better only when two problems are close enough plan matching could be the bottleneck Graphplan Partial-order general planner Constructing a planning graph before search plan graph contains all possible actions that can be taken in each time step actions that interfere with one another can coexist in the graph More efficient than other general planners in some problems Problem-specific Planning Heuristics combined during search heuristics is problem dependent cannot apply to other problems Usually outperforms general planners in specific problems Example in sliding-tile puzzle, accurate estimation of the distance between current state and goal state can speed up the search for a plan Genetic Algorithms Parallel search and optimization algorithm Inspired by the basic rule of natural selection, survival-of-the-fittest Non-deterministic algorithm randomness is incorporated during implementation Solution Formation Candidate solution is encoded as a list of genes, called chromosome 1 0 1 1 0 1 Start with a population of randomly generated chromosomes Population is evolved in every generation evaluate each chromosome select chromosomes to the next generation apply genetic operations Genetic Operation crossover Before crossover After crossover Crossover point 1 0 1 1 0 1 0 0 0 1 1 1 1 0 1 1 1 1 0 0 0 1 0 1 Genetic Operation Mutation Before mutation 1 0 1 1 0 1 After mutation 1 0 0 1 0 1 GA Procedure Initialize the population Evaluate each chromosome in the population While the stopping condition is not met select chromosomes to the next generation crossover, mutation evaluate newly generated chromosomes End while Evolutionary Computation Approach Non-deterministic algorithm Starts from a set of randomized plan Plans are evolved during generations In each generation evaluate the performance of the plan select the plans to next generation, based on performance crossover, mutation to create new plans Evolutionary Computation Approach Solution encoding a list of floating-point number, each number maps to an action in the problem number of actions can vary during search 0.8 0.5 0.3 0.2 0.5 A4 A3 A2 A1 A2 Evolutionary Computation Approach State-aware crossover crossover points are selected based on the matching of states s1 Parent 1 s2 Parent 2 Child 1 Child 2 Match(s1, s2) = true Evolutionary Computation Approach Mutation randomly select an action and replace it with a random floating-point number Before mutation 0.8 0.5 0.3 0.2 0.5 After mutation 0.8 0.5 0.6 0.2 0.5 Evolutionary Computation Approach Fitness evaluation consists of two parts: goal fitness fg and cost fitness fc goal fitness: how the solutions reach the goal state cost fitness: the total cost of the solution overall fitness = a * fg + b * fc Experimental Results Towers of Hanoi Sliding-tile puzzle can solve the 5 and 6-disk case with high probability state-aware crossover does not perform well can solve 3*3 problem case with high probability state-aware crossover perform much better since a looser definition of matching state is used Performance scalability is not good Heuristics may be helpful to improve the References Artificial Intelligence: A Modern Approach. Stuart Russell and Peter Norvig. Prentice Hall. Artificial Intelligence: A New Symthesis. Nils Nilsson. Kaufmann. Intelligent Planning: A Decomposition and Abstraction Based Approach. Qiang Yang. Springer. Internet-Based Workflow Management: Towards a Semantic Web. Dan C. Marinescu. Wiley, 2002. References Plan reuse versus plan generation: a theoretical and empirical analysis. B. Nebel, J. Koehler. Journal of Artificial Intelligence 76 (1995), 427-454. Fast planning through planning graph analysis. A. L. Blum, M. L. Furst Journal of Artificial Intelligence 90 (1997), 281300. Planning as heuristic search. B. Bonet, H. Geffner. Journal of Artificial Intelligence 129 (2001), 5-33. What it is, What it could be, An introduction to the Special Issue on Planning and Scheduling. D. McDermott, J. Handler. Journal of Artificial Intelligence 76 (1995), 1-16. Concluding Words Failing to plan is planning to fail --Effie Jones