Download 5.3 Law of Sines and Triangulation

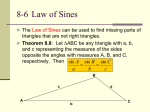
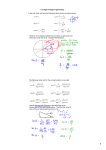
Triangulation and the Law of Sines
A triangle has three sides and three angles; their values provide six pieces
of information about the triangle.
In ordinary geometry, most of the time three pieces of information are
sufficient to give us the other three pieces of information.
Elementary Functions
Part 5, Trigonometry
Lecture 5.3a, The Laws of Sines and Triangulation
In order to more easily discuss the angles and sides of a triangle, we will
label the angles by capital letters (such as A, B, C) and label the sides by
small letters (such as a, b, c.)
Dr. Ken W. Smith
We will assume that a side labeled with a small letter is the side opposite
the angle with the same, but capitalized, letter.
For example, the side a is opposite the angle A.
Sam Houston State University
2013
We will also use these letters for the values or magnitudes of these sides
and angles, writing a = 3 feet or A = 14◦ .
Smith (SHSU)
Elementary Functions
2013
1 / 26
Three Bits of a Triangle
Smith (SHSU)
Elementary Functions
2013
2 / 26
AA and AAA
Suppose we have three bits of information about a triangle. Can we
recover all the information?
AAA
If the 3 bits of information are the magnitudes of the 3 angles, and if we
have no information about lengths of sides, then the answer is No.
Given a triangle with angles A, B, C (in ordinary Euclidean geometry) we
can always expand (or contract) the triangle to a similar triangle which
has the same angles but whose sides have all been stretched (or shrunk)
by some constant factor.
If we know the values of two angles then since the angles sum to π
(= 180◦ ), we really know all 3 angles.
So AAA is really no better than AA!
We need to know at least one of the sides.
This “Angle-Angle-Angle” information (AAA) is not enough information
to describe the entire triangle.
However, we will discover that in almost every other situation, we can
recover the entire triangle.
Smith (SHSU)
Elementary Functions
2013
3 / 26
Smith (SHSU)
Elementary Functions
2013
4 / 26
ASA and AAS
The Law of Sines and ASA
Suppose we know two angles and one side. If the known side is between
the two angles we abbreviate this ASA.
If we know two angles and one side, but the known side is not between the
two angles, then we are in the Angle-Angle-Side (AAS) situation and we
can also recover the remaining bits of the triangle.
The law of sines says that give a triangle 4ABC, with lengths of sides
a, b and c then
sin B
sin C
sin A
=
=
(1)
b
c
a
Why is this true?
We do this using the Law of Sines.
Smith (SHSU)
Elementary Functions
2013
5 / 26
The Law of Sines
Smith (SHSU)
Elementary Functions
2013
6 / 26
2013
8 / 26
The Law of Sines
Start with a triangle with vertices A, B, C
Draw a perpendicular from the vertex C onto the side AB and let D
represent the right angle formed there.
If h is the height of the triangle then
sin A =
h
b
and sin B = ha .
Solve for h:
h = b sin A and h = a sin B.
Since both b sin A and a sin B are equal to h then
b sin A = a sin B.
h
h
sin A = and sin B = .
b
a
Dividing both sides by ab we have
sin A
a
=
sin B
b .
=
sin C
c
A similar argument tells us that
sin A
a
Smith (SHSU)
Elementary Functions
2013
7 / 26
Smith (SHSU)
Elementary Functions
The Law of Sines
Two Angles and the Law of Sines
sin A
sin B
sin C
=
=
a
b
c
Smith (SHSU)
Elementary Functions
(2)
2013
9 / 26
If we know two angles of a triangle, then since the three angles add to
180◦ = π then we can figure out the third angle. As long as we know one
more bit of information, the length of a side, then the law of sines gives us
the length of all sides.
In our abbreviated notation for the known information, this includes the
cases ASA and AAS, that is, the cases in which we know two angles and
an included side or two angles and a side not between them. These cases
are equivalent since, essentially, we know all three angles once we know
two.
Smith (SHSU)
Elementary Functions
2013
10 / 26
Some Worked Problems.
Some Worked Problems.
Use the Law of Sines to solve the following triangles.
A = 62◦ , B = 74◦ , c = 14 feet
Solve the triangle A = 60◦ , B = 70◦ , c = 10 feet
Solution. If A = 62◦ , B = 74◦ , c = 14 feet then C = 54◦ . Then, by the
law of sines,
Solution. If A = 60◦ , B = 70◦ , c = 10 feet then C = 50◦ since the sum of
the angles of a triangle is 180◦ .
By the law of sines,
sin 54◦
sin 62◦
sin 75◦
=
=
14
a
b
sin 60◦
sin 70◦
sin 50◦
.
=
=
a
b
10
so
a=
14 sin 62◦
14 sin 75◦
≈
15.28
feet
and
b
=
≈ 16.72 feet.
sin 54◦
sin 54◦
Smith (SHSU)
Elementary Functions
2013
So a =
11 / 26
10 sin 60◦
10 sin 70◦
=
11.31
feet
and
b
=
= 12.27 feet
sin 50◦
sin 50◦
Smith (SHSU)
Elementary Functions
2013
12 / 26
Law of Sines
Elementary Functions
Part 5, Trigonometry
Lecture 5.3b, The Laws of Sines and Triangulation
In the next presentation, we will continue to look at the Law of Sines,
investigating the SSA case.
Dr. Ken W. Smith
(End)
Sam Houston State University
2013
Smith (SHSU)
Elementary Functions
2013
13 / 26
The law of sines and SSA
Smith (SHSU)
Elementary Functions
2013
14 / 26
Some Worked Problems
If we know only one angle of a triangle but two sides, sometimes the Law
of Sines is sufficient.
Solve the following triangle. (Find all sides and all angles.)
A = 30◦ , a = 6 feet, b = 8 feet
Solution. To solve A = 30◦ , a = 6 feet, b = 8 feet apply the law of sines:
sin 30◦
6
To use the laws of sines, we need one of the sides to be opposite the
known angle.
=
sin B
8
=
sin C
c
This forces
In this case, our information is often abbreviated SSA – we know two
sides and then an angle not between them.
sin B =
We do have to be a bit careful here. Just because we know the sine of an
angle does not mean we know the value of the angle!
There could be two angles with the same sine!
8 sin 30◦
6
=
2
3
so B is either sin−1 ( 23 ) ≈ 41.81◦ or B = 180 − 41.81◦ = 138.19◦ .
If B = 41.81◦ then C = 108.19◦ . If B = 138.19◦ then C = 11.81◦ .
6 sin C
By the law of sines c = sin
30◦ = 12 sin C.
If C = 108.19◦ then c = 12 sin 108.19◦ = 11.40
But if C = 11.81◦ then c = 12 sin 11.81◦ = 2.46
Smith (SHSU)
Elementary Functions
2013
15 / 26
Smith (SHSU)
Elementary Functions
2013
16 / 26
Some Worked Problems
Some Worked Problems
Solve the triangle A = 60◦ , a = 10 feet, c = 12 feet
Solutions. If A = 60◦ , a = 10 feet, c = 12 feet then by the law of sines
We solved the triangle A = 30◦ , a = 6 feet, b = 8 feet:
sin 60◦
sin C ◦
=
10
12
There are two solutions, two triangles:
So
√
12 sin 60◦
3 3
sin C =
=
≈ 1.039 > 1.
10
5
A
B
C
a b
c
◦
◦
◦
30
41.81
108.19 6 8 11.41
◦
◦
30 138.19
11.81◦ 6 8 2.46
There is no angle with sine greater than 1 so there is no solution;
This triangle cannot exist.
Smith (SHSU)
Elementary Functions
2013
17 / 26
Some Worked Problems
Smith (SHSU)
Elementary Functions
2013
18 / 26
Some Worked Problems
Solve the triangle a = 10, b = 6, B = 20◦ .
Solution. Use the Law of Sines to see that A could be either A = 34.75◦
or A = 145.25◦ ,
Solve the triangle b = 12, c = 10, C = 60◦ .
Then C = 125.25◦ or C = 14.75◦ .
Solution. By the Law of Sines, sin B =
Finally use the Law of Sines to finish off the problem.
12
3√
(sin 60◦ ) =
3 ≈ 1.039.
10
5
Since the sine of B cannot be greater than one,
no such triangle is possible.
There are two answers. Both must be listed.
a = 10, b = 6, c = 14.33, A = 34.75◦ , B = 20◦ , C = 125.25◦
(The length of b is not large enough to “reach” the side a.)
and
a = 10, b = 6, c = 4.47, A = 145.25◦ , B = 20◦ , C = 14.75◦ .
Smith (SHSU)
Elementary Functions
2013
19 / 26
Smith (SHSU)
Elementary Functions
2013
20 / 26
Some Worked Problems
Triangulation
Solve the triangle b = 12, c = 10, C = 45◦ .
Solution. By the Law of Sines either B ≈ 58.06◦ or B ≈ 121.95◦ ,
Finally use the Law of Sines to finish off the problem.
One can often measure distance to an object by working out a baseline
and then measuring the angles formed by lines from the distant object to
the ends of the baseline.
There are two answers. Both must be listed.
This technique is called ”triangulation”.
Then A ≈ 76.95◦ or A ≈ 13.05◦ .
a = 13.78, b = 12, c = 10, A = 76.95◦ , B = 58.45◦ , C = 45◦ ,
This is a classic case of ASA and is perfect for the law of sines.
and
a = 3.19, b = 12, c = 10, A = 13.05◦ , B = 121.95◦ , C = 45◦
Smith (SHSU)
Elementary Functions
2013
21 / 26
Smith (SHSU)
Elementary Functions
2013
22 / 26
Triangulation
Triangulation
Suppose that a ship is out in the harbor. Standing at the east end of the
dock, a compass reveals that the ship is at a bearing of 30◦ east of north.
But if one walks 200 yards west of the dock, the ship is now at a bearing
of 40◦ east of north.
Draw an east-west baseline representing the 200 yards and then draw lines
from the ends of the baseline to the ship. We have a triangle in which the
vertex on the west side of the baseline has an (interior) angle of
90◦ − 40◦ = 50◦ . The vertex on the east side of the baseline has an angle
of 90◦ + 30◦ = 120◦ . Call the length of the baseline c = 200, and so we
have angles A = 50◦ and B = 120◦ .
How far is the ship from the dock?
Smith (SHSU)
Elementary Functions
2013
23 / 26
Smith (SHSU)
Elementary Functions
2013
24 / 26
Triangulation
The Law of Sines and Triangulation
Let us use C to represent the angle 10◦ at the vertex of this triangle where
the ship sits. Then the side c is the 200 yard baseline and the angles A
and B are 50◦ and B = 120◦ .
We can solve this problem by the Law of Sines and see that
a = 882, b = 997.45 So the ship is 882 yards from the east end of the dock.
In the next presentation we look at the Law of Cosines
(End)
Smith (SHSU)
Elementary Functions
2013
25 / 26
Smith (SHSU)
Elementary Functions
2013
26 / 26