Download The Effects of Drain-Bias on the Threshold Voltage Instability in

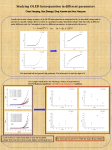
IEEE ELECTRON DEVICE LETTERS, VOL. 29, NO. 2, FEBRUARY 2008
155
The Effects of Drain-Bias on the Threshold Voltage
Instability in Organic TFTs
Hsiao-Wen Zan, Member, IEEE, and Shin-Chin Kao
Abstract—In this letter, the influence of drain bias on the threshold voltage instability in pentacene-based organic thin-film transistors (OTFTs) was studied. By applying different drain biases
to adjust the channel carrier concentration in linear mode, the
threshold voltage shift was found to be proportional to the carrier
concentration. The experimental data can be well quantitatively
explained by the drain bias-stress theory developed for a-Si TFTs.
The outcome gives the insight of the degradation mechanism of
OTFTs and is important for the design of OTFT pixel circuit,
OTFT analog amplifiers, or OTFT active loads.
Index Terms—Bias-stress effect, organic thin-film transistor
(OTFT), pentacene, reliability.
I. INTRODUCTION
ECENTLY, the development of organic thin-film transistors (OTFTs) has drawn lots of attentions. Field-effect
mobility comparable to that of a-Si TFTs can be obtained under a low operation voltage [1], [2]. However, the reliability
of OTFTs remains a significant issue. Even when devices are
encapsulated or operated in the inert environment, the threshold
voltage (VT ) tends to shift under continuous bias. This biasstress effect (BSE) was observed in OTFTs with different organic active materials, different gate insulators, and different
structures [3]. It was also found that the BSE was reversible
after the removal of bias, and the reverse process was enhanced
by applying opposite polarity bias or light irradiation.
Several mechanisms have been proposed to explain the BSE,
including charge trapping, ion migration, charged-state creation, and the formation of bound hole pairs (bipolaron) [4].
For OTFTs with organic dielectric, charge trapping and ion
migration were found to be dominant [5]. For OTFTs with thermally grown SiO2 as the gate dielectric, charged-state creation
or bipolaron formation within the organic semiconductor film,
near the dielectric interface, is usually believed to be responsible for VT shifts [3]. More specifically, Northrup and Chabinyc
had proposed that the state creation was due to the formation of
oxygen- or hydrogen-related defects, such as C−H2 , OH , and
C−HOH in organic semiconductors [6]. The bipolarons, proposed by Salleo et al., are the less mobile bound hole pairs that
deplete the accumulation channel of mobile holes and cause an
increase in the VT .
R
Manuscript received September 3, 2007. This work was supported in part by
the AU Optronics Corporation, in part by the National Science Council (NSC96-2221-E-009-127-MY2), and in part by the Ministry of Economic Affairs
(MOEA-96-EC-17-A-07-S1-046). The review of this letter was arranged by
Editor Y. Taur.
The authors are with the Department of Photonics and Display Institute, National Chiao Tung University, 300 Hsinchu, Taiwan, R.O.C. (e-mail: hsiaowen@
mail.nctu.edu.tw; [email protected]).
Digital Object Identifier 10.1109/LED.2007.914081
Both the state creation and the bipolaron formation suggest
that the reaction rate should be proportional to the carrier concentration. Thus, the gate-BSE can be explained. However, to
the best of our limited knowledge, there is no other observation
directly validating the proportionate relationship between the
reaction rate and the carrier concentration. In linear mode, drain
bias can be useful to adjust the carrier concentration. Thus, its
influence on the BSE of OTFTs is worth investigating. Although
the drain bias effect in OTFTs with organic dielectric had been
studied to discuss its influence on ion migration [5], the effect
on OTFTs with stable dielectric had not been carefully investigated before. This letter clearly demonstrates that a modified
BSE model (including drain-bias effects) in a-Si TFTs can be
applied on OTFTs with SiO2 dielectric. The result is useful for
the development of OTFTs in organic electronics.
II. EXPERIMENTAL
In this letter, conventional top-contact pentacene-based
OTFTs were used. To serve as the gate dielectric, 100-nm-thick
thermal oxide was grown on heavily doped Si wafers. Then,
pentacene obtained from Aldrich without any purification was
evaporated through shadow mask onto the thermal oxide to form
the active layer. The deposition rate was controlled at 0.5 Å/s,
while the substrate temperature was kept as 70 ◦ C. After the
formation of 100-nm-thick pentacene, 100-nm-thick gold was
deposited through the shadow mask to form the source/drain
contacts. The device channel width and length were defined as
1000 and 600 µm, respectively. Two series of bias-stress measurements were performed: one with zero drain bias and various
gate biases, and the other with a fixed gate bias and different
drain biases.
III. RESULTS AND DISCUSSION
First, we analyze the BSE with zero drain bias. With
source and drain connected to ground, various gate biases
were used as the stress conditions (VDS = 0 V, VG − VTini =
−5, −10, and − 15 V, where VTini is the initial threshold voltage). The linear-region transfer characteristics of the devices
before stress and after 2000 s stress are depicted in Fig. 1(a). All
the devices exhibit similar original characteristics, so only one
curve is shown to represent the characteristics before stress. Obviously, the gate-bias stress causes a shift of the transfer characteristics, while the subthreshold swing keeps almost unchanged.
The shift of threshold voltage VT and the shift of field-effect mobility µFE are shown as a function of stress time in Fig. 1(b)
and (c), respectively. µFE is not affected by the stress, while VT
is drastically changed. Such a phenomenon is often believed to
0741-3106/$25.00 © 2008 IEEE
156
IEEE ELECTRON DEVICE LETTERS, VOL. 29, NO. 2, FEBRUARY 2008
Fig. 1. (a) Transfer characteristics of OTFTs before and after 2000 s gate bias stress. The stress conditions are: V G − V Tin i = −5, −10, and −15 V, V D S = 0 V.
(b) Shift of threshold voltage and (c) the shift of mobility as a function of stress time.
Fig. 2. (a) Shift of mobility. (b) Shift of threshold voltage as a function of stress time when different drain biases (V D S = 0, 5, 10, and 15 V) were added to the
bias-stress measurement while the gate bias was fixed as V G − V Tin i = −15 V.
be caused by the generation of deep states with long discharge
time that degrade VT . The shallow traps that would affect µFE
may not be changed by the gate bias stress [7]. The power-law
dependence between the threshold voltage shift and the stress
time is also found in Fig. 1(b). This can be explained by the
approximation of the OTFT BSE model, in which the stretched
exponential function reduces to the simple power-law function
when the stress time is much less than the effective trapping
time τ [8].
Then, different drain biases (VDS = 0, 5, 10, and 15 V)
were added to the bias-stress measurement while the gate bias
was fixed as VG − VTini = −15 V. The shift of µFE is plotted
as a function of stress time in Fig. 2(a). Unchanged µFE is
observed, and consequently, the influence of drain-bias stress on
ZAN AND KAO: EFFECTS OF DRAIN-BIAS ON THE THRESHOLD VOLTAGE INSTABILITY IN ORGANIC TFTs
Fig. 3. Threshold voltage shift ratio (∆V T D /∆V T 0 ) and the normalized channel charge (Q G /Q G 0 ) as a function of stressed drain bias, while the stressed
gate bias was fixed as V G − V Tin i = −15 V.
157
tion of drain bias in Fig. 3. The calculated normalized channel charge defined as QG /QG 0 is also shown in Fig. 3, where
QG is the channel charge when VDS is varied and QG 0 is the
channel charge when VDS = 0. The equations used to calculate
QG and QG 0 are expressed in Ref [9]. Good agreement can
be observed between ∆VTD /∆VT 0 and the calculated QG /QG 0
curve. The result verifies the proportionate relationship between
the defect creation rate and the carrier concentration. Also, the
result suggests that convergent data can be obtained by plotting
the restored threshold voltage shift ∆VTD (QG 0 /QG ) as a function of stress time, as shown in Fig. 4. The restored threshold
voltage shift excludes the drain bias effect and can be used to
extract the parameters associated with the defect creation kinetics. For example, when the stretched exponential function
is used, the dispersion parameter β can be obtained by plotting
log{− ln[1 − ∆VTD (QG 0 /QG )/(VGS − VTini )]} as a function of
log(t) in the inset of Fig. 4. Detailed description of the stretched
exponential function can be found in Ref. [8].1 The parameters
extracted from our devices are given as follows.
IV. CONCLUSION
This letter presents the drain bias influence on VT of OTFTs
in bias stress measurement. It verifies that, for OTFTs with SiO2
dielectric, the shift of VT is proportional to the channel charge
amount as in a-Si TFTs. The results can be used to predict the
reliability of OTFTs when OTFTs are applied on analog circuits
such as the OLED pixel circuit.
REFERENCES
Fig. 4. Restored threshold voltage shift as a function of stress time.
The theoretical curve given by ∆V T D × (Q G 0 /Q G ) = (V G − V Tin i ){1 −
exp[−(t/τ )β]]} is also plotted with the parameters given in footnote 1. The
dispersion parameter β can be obtained by plotting log{− ln[1 − ∆V T D
(Q G 0 /Q G )/(V G S − V Tin i )]} as a function of log(t) as shown in the inset.
the shallow traps can be excluded. The influence of drain-bias
stress on the VT , however, is significant. As shown in Fig. 2(b),
the shift of VT is suppressed when the drain bias becomes more
negative. All the relationships depicted in Fig. 2(b) follow the
power-law dependence with identical slope. According to the
BSE model, the slope represents the dispersion parameter β
that influences the relaxation and the dispersive transport of
disorder system. Identical β value implies that the microscopic
processes of the state creation such as the impurity diffusion or
the defect creation kinetics should be independent of the drain
bias. The influence of drain bias on the carrier concentration is
believed, as in a-Si TFTs, to be the dominant reason that causes
the shift of threshold voltage to be dependent on VDS .
To quantitatively discuss this relationship, for a given VGS ,
we define the threshold voltage shift ratio (∆VTD /∆VT 0 ) as
the ratio between the threshold voltage shift with various VDS
stress (∆VTD ) and the threshold voltage shift with zero drainbias stress (∆VT 0 ). Then, we plot ∆VTD /∆VT 0 as a func-
[1] H. Klauk, M. Halik, U. Zschieschang, G. Schmid, and W. Radlik, “Highmobility polymer gate dielectric pentacene think film transistors,” J. Appl.
Phys, vol. 92, no. 9, pp. 5259–5263, Nov. 2002.
[2] H.-W. Zan, K.-H. Yen, P.-K. Liu, K.-H. Ku, C.-H. Chen, and J. Hwang,
“Low-voltage organic thin film transistors with hydrophobic aluminum
nitride film as gate insulator,” Org. Electron., vol. 8, pp. 450–454, 2007.
[3] A. Salleo and R. A. Street, “Light-induced bias stress reversal in polyfluorene thin-film transistors,” J. Appl. Phys., vol. 94, no. 1, pp. 471–479,
Jul. 2003.
[4] R. A. Street, A. Salleo, and M. L. Chabinyc, “Bipolaron mechanism
for bias-stress effects in polymer transistors,” Phys. Rev. B, vol. 68,
pp. 085316-1–085316-7, 2003.
[5] S. J. Zilker, C. Detcheverry, E. Cantatore, and D. M. de Leeuw, “Bias
stress in organic thin-film transistors logic gates,” Appl. Phys. Lett.,
vol. 79, pp. 1124–1126, 2001.
[6] J. E. Northrup and M. L. Chabinyc, “Gap states in organic semiconductors:
Hydrogen- and oxygen-induced states in pentacene,” Phys. Rev. B, vol. 68,
pp. 041202-1–041202-4, 2003.
[7] J. B. Changa and V. Subramanian, “Effect of active layer thickness on bias
stress effect in pentacene thin-film transistors,” Appl. Phys. Lett., vol. 88,
pp. 233513-1–233513-3, 2006.
[8] G. Gu, M. G. Kane, and S.-C. Mau, “Reversible memory effects and
acceptor states in pentacene-based organic thin-film transistors,” J. Appl.
Phys., vol. 101, no. 1, pp. 014504-1–014504-9, 2007.
[9] K. S. Karim, A. Nathan, M. Hack, and W. I. Milne, “Drain-bias dependence
of threshold voltage stability of amorphous silicon TFTs,” IEEE Electron
Device Lett, vol. 25, no. 4, pp. 188–190, Apr. 2004.
1 The dispersion parameter β can be obtained by plotting log{− ln[1 −
∆V T D (Q G 0 /Q G )/(V G S − V Tin i )]} as a function of log(t) in the inset of
Fig. 4. After extracting β = 0.283 and defining the attempt to escape frequency,
v = 105 Hz, the effective trapping time τ and the mean activation energy for
the defect generation E A can be determined by fitting ∆V T D (Q G 0 /Q G ) with
the stretched exponential function. The resulting E A is 0.57 eV and τ is 36127
s at room temperature.