* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Week_10
Euler angles wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Compass-and-straightedge construction wikipedia , lookup
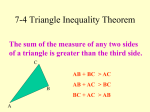
WEEK 10 (assignments 34-37) 11/01 homework (#34)* (note this homework was assigned on 11/01-week 10) Construct a total of five (5) triangles using the methods taught in class for SSS and SAS. Label all points on the image triangle and three parts that are congruent to the parts in the original side. (1) ΔABC with AC=2AB,BC=1½AB (2) ΔABC with mB = 90 degrees by “pulling a right angle from a point ON the line”, AC=2AB (3) ΔDEF with mE = 45 degrees by bisecting a 90, EF= ½ED (4) ΔGHI with mH = 60 degrees by using the “equilateral triangle” method, GI=2GH (5) ΔJKL with mK = 30 degrees by bisecting a 60, KL= ¼KJ Note Label all the points and congruent parts on the image construction 11/2 homework (SSS triangle construction)#35 Construct six (6) triangles given certain parts. The original sides will have regular letters as labels (ex: ABC) the image will have the primes for these letters (ex: A’B’C’) For each set of originals, use a side AB that is three lines (of lined paper) long. Then make the originals using the rules below. For each there are two parts: (A) (B) Do the triangle inequality test (on a ray add the two shorter segments together and subtract the longest segment). If there is any length left “DIFF” then proceed to (B), otherwise state “DOES NOT PASS” Construct the triangle on an image ray using the following steps: (1) Copy the longest segment onto your ray (ex AB copies to A’B’) (2) Make an arc with a radius equal to one of the lengths of one of the two remaining original sides (ex: BC) – note that this arc MUST be centered at the B’ point on your image. (3) Make an arc with the radius equal to the length of the last remaining original side (ex: CA) – note that this arc MUST be centered at the A’ point on your image. (4) Where the two arcs from steps (c) and (d) intersect is your third point C’. Label it C’ and connect it to A’ and B’ Note: as you make the construction, label your new points (with the primes) and put tic marks on the originals and image lengths that are congruent. Here are the rules for your three original sides: (1) DE=AB, EF=2AB, FD=4AB (2) HI=AB, IJ=3AB, JH=AB (3) KL=AB, LM=1½AB, MK=2AB (4) NO=2AB, OP=1½AB, JH=AB (5) QR=2AB, RS=3AB, SQ=2½AB (6) TU=½AB, UV=2AB, VT=AB (EC) WX=1¼AB, XY=1½AB, YW=¾AB 11/4 homework (Review for Friday’s Test)#36 (1) Construct five triangles (a) (b) (c) (d) (e) Acute with angles of 60,75, and 45 degrees (construct the angles, then copy onto an image ray (Note: you actually only need to make two of the three) Right (one angle is 90 degrees) Obtuse (one angle is 105 degrees) Isosceles with both base angles = 75 degrees each (construct the angle then copy it to both ends of an image line segment. Isosceles with a vertex angle of 45 degrees (construct the angle, then make both sides congruent (2) Construct an altitude from vertex A of triangle ABC (3) Construct a median from vertex M of triangle MNO Note: instructions for medians and altitudes in in Homework from Week 8 11/5 homework (SAS and ASA triangle construction)#37 Construct six (6) triangles given certain parts. The original sides will have regular letters as labels (ex: ABC) the image will have the primes for these letters (ex: A’B’C’). Follow the steps given in class which are repeated on the next page. (SAS triangle construction) Given the following original parts: two sides and one angle construct the image triangle (1) B acute, AB≠CB construct ΔA′B′C′ (2) D obtuse, DE≠EF construct ΔE′F′G′ (3) I Right, HI≠IG construct ΔG′H′I′ (ASA triangle construction) Given the following original parts: two angles and one side construct the image triangle Two parts (A) Triangle Sum Test (B) If TS Test Passes, then construct image triangle (1) Both A and B acute, AB construct ΔA′B′C′ (2) R right, S acute, RS construct ΔR′S′T′ (3) O obtuse P acute, OP construct ΔO′P′Q′ (ec) M right, N acute, LM construct ΔL′M′N′ 11/5 homework (HL triangle construction)#38 Construct six (6) triangles given certain parts. The original sides will have regular letters as labels (ex: ABC) the image will have the primes for these letters (ex: A’B’C’). Follow the steps given in class which are repeated on the next page. For each set of originals, use a side AB that is three lines (of lined paper) long. Then make the originals using the rules below. For each there are two parts: (HL triangle construction) Given the following original parts construct a right triangle on the image side (1) Hypotenuse DE=2AB and leg FE=½AB construct ΔD′E′F′ (2) Hypotenuse FG=1½AB and leg FE=AB construct ΔE′F′G′ (3) Hypotenuse GH=2½AB and leg GI=2AB construct ΔG′H′I′ (Other triangle construction) Given the following original parts construct the Stated image triangle (4) Right Triangle with leg JK=2AB and mJ=30 degrees construct ΔJ′K′L′ (5) Isosceles Triangle with leg MN=MO=2AB and mM=30 degrees construct ΔM′N′O′ Note: M is the vertex angle (6) Isosceles Triangle with leg QR=QS=AB and mR=45 degrees construct ΔQ′R′S′ Note: R is one of the base angles (ec) Isosceles Triangle with base TU=2AB and mV=75 degrees construct ΔT′U′V′ Note: V is the vertex angle (so you need to bisect its supplement to get one of the base angles) How to construct triangles using three sides (SSS) The original sides will have regular letters as labels (ex: ABC) the image will have the primes for these letters (ex: A’B’C’) (SSS triangle construction) Given three sides (ex AB, BC, and CA) (a) Make the three sides as your originals, and make a ray on your image side. Before going to the actual construction you must do the Triangle Inequality Test. To do this test you must prove that the sum of any two sides is greater than the length of the third side. To do the triangle inequality test on a ray add the two shorter segments together and subtract the longest segment. If there is any length left label it “DIFF” then proceed to the next step, otherwise state “DOES NOT PASS TI TEST” (b) (c) (d) (e) Copy the longest segment onto the image ray labeling both endpoints (ex AB copies to A’B’) Make an arc with a radius equal to one of the lengths of one of the two remaining original sides to one endpoint on the image ray. Check that the one of the end points of the original agrees with the letter of the image. (ex: for BC the arc MUST be centered at the B’ point on your image) Make an arc with the radius equal to the length of the last remaining original side to the other endpoint of the image(ex: for CA the arc MUST be centered at the A’ point on your image) Where the two arcs from steps (c) and (d) intersect is your third point C’. Label it C’ and connect it to A’ and B’, and put tic marks on the sides to show congruence Note: as you make the construction, label your new points (with the primes) and put tic marks on the originals and image lengths that are congruent. Videos: (warning - this video doesn’t seem to laod very good … 11/01/10) (1) Triangle inequality: http://teachertube.com/viewVideo.php?video_id=11442&title=Types_of_Triangles How to construct triangles using two sides and one angle (SAS) or two angles and one side (ASA) as your originals parts The original parts will have regular letters as labels (ex: ABC) the image will have the primes for these letters (ex: A’B’C’) (SAS triangle construction) Given two sides (ex AB, BC) and one angle (ex: B) (a) Make the two sides and the angle as your originals, and make a ray on your image side. (b) Copy the angle onto the ray. Hint: Use the length of one of your original segments as your measuring arc, picking one with an end point that agrees with the letter of your angle. (c) After copying your angle. Label the new points for the angle, and the one side you used for the measuring arc (you can pick either side of your angle). Put tic marks for the angles and the side to show congruence to the originals (d) Span your second side, and place the bulls-eye over the prime letter that agrees with one of the original side’s two endpoints. (e) The intersection of the arc in step (d) and the extended ray or the other side of the angle is your third point. Label it, and connect it to the remaining point to complete the triangle (ASA triangle construction) Given two angles (ex C, and B) and one angle (ex:CB) (a) Make the two angles and one side as your originals, and make a ray on your image side. Before going to the actual construction you must do the Triangle Sum Test. To do this test you must add the two original angles together to show that they sum to less than 180 degrees. If the test passes (your two angles make less than a straight line) then proceed to the next step, otherwise state “DOES NOT PASS ΔSUM TEST” (b) (c) (d) (e) Copy the original side onto the image ray labeling both endpoints Copy the both angles onto the two endpoints that agree with the letter for the original angle. Hint: You can use the same measuring ray for both angles. Therefore you make a total four arcs with the same radius (two on your originals, and two on the endpoints for your image side.) After copying your angles, put tic marks for the angles to show congruence to the originals. Extend the sides to meet at your third vertex. The intersection of the new sides in step (d) is your third point. Label it to complete the triangle. How to construct triangles using Hypotenuse Leg (HL) as your originals parts The original parts will have regular letters as labels (ex: ABC) the image will have the primes for these letters (ex: A’B’C’) (HL triangle construction) Given two sides one identified as a Hypotenuse and the other as a Leg and (ex Hyp: AB, Leg: BC) (a) First you need to figure out which letter corresponds to your right angle. It is always the one letter NOT on the hypotenuse. In the example the angle Hypotenuses is AB, so the missing letter is the other letter in the leg – C (b) On your image ray you need to pull a right angle from the point you found in step (a). When doing this construction, use the leg length as your semicircle, then label your right angle with a “box” and letter, and then the leg with the other endpoint and make the tic marks on the leg to agree with that on your original. For the example: right angle is C’, and the leg has B’ at the other endpoint. (c) Span the hypotenuse, and place the bulls-eye over the endpoint of the leg in step (b). Make an arc to pass thru the other side of your right angle. Note: you may need to extend that other side long enough so it passes thru the arc. Where the arc passes the side label the last point and make the tic marks on the hypotenuse to agree with the original (Isosceles triangle construction) There are numerous ways to construct isosceles triangles based on the original parts. Here are a few examples (1) Given the vertex angle (ex C) and one leg (ex:CB) Copy the vertex angle using the leg length as the measuring arc. The base side is at the same point that the spanning arc meets the measuring arc. (like SAS) (2) Given a base angle (ex C) and the base(ex:CB) Copy the base CB, then copy the base angle on both endpoints (like ASA) (3) Given a base angle (ex C) and the one leg (ex:CB) First find the vertex angle by finding the supplement to the twice the base angle. Measure of vertex angle = 180 - 2mC. Then just follow the steps for (1) (4) Given a vertex angle (ex C) and the base(ex:AB) First find a base angle by bisecting the supplement to the vertex angle. Measure of base angle = ½(180-mC). Then just follow the steps for (2)