* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Triangles
Technical drawing wikipedia , lookup
Multilateration wikipedia , lookup
Perceived visual angle wikipedia , lookup
Golden ratio wikipedia , lookup
Apollonian network wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
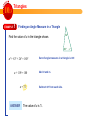
10. 3 Triangles Activity 1 2 You can find the sum of the angle measures in a triangle. Cut a triangle from the corner of a piece of paper. Label the corners A, B, and C. A C B Tear the corners off the triangle. A 3 B C Rearrange A, B, and C so that they are adjacent. Then make a conclusion about the angles of the triangle. A B C C B A C B A In the activity, you found that the sum of the angle measurements in is 180º. The sum of the angle measurements in any triangle is 180º. ABC 10. 3 EXAMPLE Triangles 1 Finding an Angle Measure in a Triangle Find the value of x in the triangle shown. 26º 83º xº + 83º + 26º = 180º x + 109 = 180 x = 71 ANSWER xº Sum of angle measures in a triangle is 180º. Add 83 and 26. Subtract 109 from each side. The value of x is 71. 10. 3 Triangles Interior and Exterior Angles The three angles of any triangle are called interior angles. The sides of a triangle can be extended to form angles outside of the triangle that are adjacent and supplementary to the interior angles. These angles are called exterior angles. exterior angle interior angles You can use the measures of interior angles to find the measures of exterior angles. 10. 3 EXAMPLE Triangles 2 Finding the Measure of an Exterior Angle Find the value of y in the figure. 55º To find the value of y, use the fact that adjacent interior and exterior angles of a triangle are supplementary. y º + 35º = 180º y = 145 ANSWER Definition of supplementary angles Subtract 35 from each side. The value of y is 145. 35º yº 10. 3 Triangles You can classify any triangle by the measures of its interior angles. Classifying Triangles by Angle Measures Acute Triangle Right Triangle An acute triangle A right triangle has three acute has one right angles. angle. 60º 70º Obtuse Triangle An obtuse triangle has one obtuse angle. 120º 50º 50º 40º 35º 25º 10. 3 Triangles Congruent Sides Just as congruent angles have the same measure, congruent sides of a triangle have the same length. You can use special marks to indicate that two sides or two angles of a triangle are congruent. X Y Z In the triangle above, the marks show that XY XZ and that Y Z. You can classify any triangle by the lengths of its sides. 10. 3 Triangles Classifying Triangles by Side Lengths Equilateral Triangle Isosceles Triangle An equilateral triangle has 3 congruent sides. An isosceles triangle has at least 2 congruent sides. 8m 9 in. 9 in. A scalene triangle has no congruent sides. 5 ft 5m 9 in. Scalene Triangle 8m 14 ft 11 ft 10. 3 EXAMPLE Triangles 3 Classifying a Triangle by Angle Measures Classify the triangle formed by the plant hanger by its angle measures. The triangle has one right angle, so it is a right triangle. 10. 3 EXAMPLE Triangles 3 Classifying a Triangle by Angle Measures Classify the triangle formed by the plant hanger by its angle measures. The triangle has one right angle, so it is a right triangle. EXAMPLE 4 Classifying a Triangle by Side Lengths 36 in. Classify the triangle by the lengths of its sides. 36 in. All three sides of the triangle are congruent, so the triangle is both isosceles and equilateral. 36 in.