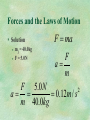* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Physics 4
Brownian motion wikipedia , lookup
Inertial frame of reference wikipedia , lookup
N-body problem wikipedia , lookup
Fictitious force wikipedia , lookup
Classical mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Centrifugal force wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Work (physics) wikipedia , lookup
Centripetal force wikipedia , lookup
Equations of motion wikipedia , lookup
Seismometer wikipedia , lookup
Classical central-force problem wikipedia , lookup
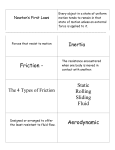
Physics Chapter 4 Forces and the Laws of Motion Forces and the Laws of Motion A force is defined as a push or pull exerted on an object. Forces can cause objects to speed up, slow down, or change direction as they move. Based on the definitions of velocity and acceleration, a force exerted on an object causes that object’s velocity to change; that is, a force causes an acceleration. Forces and the Laws of Motion How can you cause an object to move? You can push on it or you can pull on it. The push or pull is a force that you exert on the object. If you push harder on an object, you have a greater effect on its motion. The direction in which force is exerted also matters. If you push the book to the right, the book moves towards right. Forces and the Laws of Motion When considering how a force affects motion, it is important to identify the object of interest. This object is called the system. Everything around the object that exerts forces on it is called the external world. Forces and the Laws of Motion Think about the different ways in which you could move a textbook. You could touch it directly and push or pull it, or you could tie a string around it and pull on the string. These are examples of contact forces. A contact force exists when an object from the external world touches a system and thereby exerts a force on it. Forces and the Laws of Motion Contact Forces Acts on an Object by Direct Contact Field Forces Acts on an Object Without Direct Contact Examples • Magnetic Attraction and Repulsion • Gravitational Forces Forces and the Laws of Motion Agent Origin of Force Identifiable May be animate or inanimate Examples? Contact / Field Forces Forces and the Laws of Motion Free Body Diagrams Illustrate All Forces Acting on an Object • Examples? Newton’s Laws of Motion Forces and the Laws of Motion Newton’s First Law of Motion “Every Body Continues In Its State of Rest, Or of Uniform Motion In A Straight Line, Unless It is Compelled to Change That State by Forces Impressed Upon It.” Forces and the Laws of Motion Newton’s First Law of Motion “Every Body Continues In Its State of Rest, Or of Uniform Motion In A Straight Line, Unless It is Compelled to Change That State by Forces Impressed Upon It.” aka “The Law of Inertia” Forces and the Laws of Motion Inertia The Tendency of an Object to Resist a Change in Movement Mass is a Measurement of Inertia Equilibrium Net Force = 0 Forces and the Laws of Motion Force (F) Energy exerted on an object Possesses magnitude and direction May be in contact with an object May be distant from an object. Newton’s Laws of Motion Forces and the Laws of Motion Newton’s Second Law of Motion “The Acceleration of a Body is Directly Proportional to the Net Force Acting on the Body and Inversely Proportional to the Mass of the Body.” Forces and the Laws of Motion Newton’s Second Law of Motion The Greater the Force on the Object, the Greater the Acceleration of the Object The Greater the Mass of the Object, the Weaker the Acceleration of the Object Forces and the Laws of Motion Newton’s Second Law of Motion Force is Related to… • The Mass of the Object (m) • The Acceleration of the Object (a) F ma Forces and the Laws of Motion Measurement of Force SI Units • Mass - Kilogram (kg) • Distance - Meter (m) • Time - Second (s) Forces and the Laws of Motion Measurement of Force The Newton (N) • One Newton can accelerate 1 kg to 1 m/s2 • N = 1 kg*m/s2 • (F=ma) Newton’s Laws of Motion Forces and the Laws of Motion Interaction Forces Newton’s Third Law of Motion • “When an Object Exerts a Force On a Second Object, That Second Object Exerts an Equal and Opposite Force On the First Object.” Forces and the Laws of Motion Interaction Forces Interaction Pair • “Force Pair” – Non-Force-Pairs? • Two Forces in Opposite Directions with Equal Magnitude • FA ON B = -FB ON A Forces and the Laws of Motion Interaction Forces Fundamental Forces • Gravity • Electromagnetism • Strong Nuclear Force • Weak Nuclear Force Forces and the Laws of Motion Combining Forces Forces are Vectors They May Strengthen Each Other They May Cancel All or Part of Each Other They Are Cumulative Forces and the Laws of Motion Example Problem Two horizontal forces of 225N and 165N are exerted in the same direction on a crate. What is the net force on the crate? Forces and the Laws of Motion Solution 225N 165N Forces and the Laws of Motion Solution 390N Forces and the Laws of Motion Example Problem If the same two horizontal forces of 225N and 165N are exerted in opposite directions on the crate. What is the net force on the crate? Forces and the Laws of Motion Solution 225N 165N Forces and the Laws of Motion Solution 60N Forces and the Laws of Motion Example Problem If you hold a 1.0 lb object using 6.5N of upward force, what is the net force on the object? (1 lb = 0.454kg) Forces and the Laws of Motion Solution If you hold a 1.0 lb object using 6.5N of upward force, what is the net force on the object? (1 lb = 0.454kg) Fdown mg (0.454kg)(9.8m / s) 4.5N Fup Fdown 6.5 N (4.5 N ) 2.0 N Forces and the Laws of Motion Problem On Earth, a scale shows that Ben weighs 712N. What is Ben’s mass? Forces and the Laws of Motion Solution F = 712N g = 9.8m/s2 F 712 N m 72.7kg(160lb ) 2 g 9.8m / s Forces and the Laws of Motion Problem The acceleration of gravity on the moon is 1.60m/s2. What would the scale indicate that Ben weighs if he were on the moon and his mass is the same as the previous question? (72.7kg) Forces and the Laws of Motion Solution m = 72.7kg a = 1.60m/s2 F ma (72.7kg)(1.60m / s ) 116.3N 2 Forces and the Laws of Motion Problem A 2.0kg mass (ma) and a 3.0kg mass (mb) are attached to a cord that passes over a pulley. What is the acceleration of the smaller mass? Forces and the Laws of Motion Solution ma = 2.0kg mb = 3.0kg g = 9.8m/s2 ma a mb g mb a ma g (ma mb )a (mb ma ) g mb ma 3.0kg 2.0kg g 9.8m / s 2 2.0m / s 2 a 2.0kg 3.0kg ma mb Forces and the Laws of Motion Problem The maximum force a grocery sack can stand and not rip is 250N. If Elizabeth loads 20.0kg of groceries into the sack and lifts the sack from the floor to the table with an acceleration of 6.0m/s2, will the sack hold? Forces and the Laws of Motion Solution a = 6.0m/s2 m = 20.0kg Fmax = 250N ma Fnet Fapplied Fg Fapplied ma mg m(a g ) Fapplied (20.0kg)[(6.0m / s ) (9.8m / s )] 300N 2 2 Forces and the Laws of Motion Problem The instruments attached to a weather balloon have a mass of 5.0kg. The balloon is released and exerts an upward force of 98N on the instruments. What is the acceleration of the balloon and the instruments? Forces and the Laws of Motion Solution m = 5.0kg Fu = 98N g = 9.8m/s2 a=? ma Fnet Fapplied Fg ma 98 N (49 N ) 49 N up 49 N 2 a 9.8m / s up 5.0kg Forces and the Laws of Motion Problem The instruments attached to a weather balloon have a mass of 5.0kg. The balloon is released and exerts an upward force of 98N on the instruments. After the balloon has accelerated for 10.0s, the instruments are released. What is the velocity of the instruments at the moment of their release? Forces and the Laws of Motion Solution m = 5.0kg Fu = 98N g = 9.8m/s2 down a = 9.8m/s2 up v at (9.8m / s )(10.0s) 98m / s up 2 Forces and the Laws of Motion Problem The instruments attached to a weather balloon have a mass of 5.0kg. The balloon is released and exerts an upward force of 98N on the instruments. After the balloon has accelerated for 10.0s, the instruments are released. What net force acts on the instruments after their release? Forces and the Laws of Motion Solution m = 5.0kg Fu = 98N g = 9.8m/s2 down a = 9.8m/s2 up v0 = +98m/s Fg mg W 49 N Forces and the Laws of Motion Problem The instruments attached to a weather balloon have a mass of 5.0kg. The balloon is released and exerts an upward force of 98N on the instruments. After the balloon has accelerated for 10.0s, the instruments are released. When does the instrument’s velocity first become downward? Forces and the Laws of Motion Solution m = 5.0kg Fu = 98N g = 9.8m/s2 down a = 9.8m/s2 up v0 = +98m/s v v0 gt v0 v0 (98m / s) t 10.0s after release 2 g (9.8m / s ) Forces and the Laws of Motion Problem Donnie and Candice are skating. Donnie pushes Candice, whose mass is 40.0-kg, with a force of 5.0 N. What is Candice’s resulting acceleration? Forces and the Laws of Motion Solution mj = 40.0kg F = 5.0N F ma F a m F 5.0 N 2 a 0.12m / s m 40.0kg Forces and the Laws of Motion Problem Your new motorcycle weighs 2450 N. What is its mass in kilograms? Forces and the Laws of Motion Solution F = 2450N Fg mg F m g F 2450 N m 250 kg 2 g 9.8m / s Forces and the Laws of Motion Problem A 873-kg (1930-lb) dragster, starting from rest, attains a speed of 26.3m/s (58.9 mph) in 0.59 s. What is the magnitude of the average net force on the dragster during this time? Forces and the Laws of Motion Solution m = 873kg v f vi 26.3m / s 0m / s vf = 26.3m/s a 44.58m / s 2 Dt 0.59s vi = 0m/s Dt = 0.59s F ma (873kg)(44.58m / s ) 3.9 x10 N 2 4 Forces and the Laws of Motion Problem A 873-kg (1930-lb) dragster, starting from rest, attains a speed of 26.3m/s (58.9 mph) in 0.59 s. Assume that the driver has a mass of 68kg. What horizontal force does the seat exert on the driver? Forces and the Laws of Motion Solution mc = 873kg md = 68kg vf = 26.3m/s vi = 0m/s Dt = 0.59s a v f vi Dt 26.3m / s 0m / s 44.58m / s 2 0.59s F ma (68kg)(44.58m / s ) 3.1x10 N 2 3 Forces and the Laws of Motion Problem A raindrop, with mass 2.45 mg, falls to the ground. As it is falling, what magnitude of force does it exert on Earth? Forces and the Laws of Motion Solution m = 2.45x10-6 kg 6 5 Fg mg (2.45x10 kg)(9.8m / s ) 2.4 x10 N 2 Forces and the Laws of Motion Problem Male lions and human sprinters can both accelerate at about 10.0 m/s2. If a typical lion has a mass of 170 kg and a typical sprinter’s mass is 75 kg, what is the difference in the force exerted on the ground during a race between these two species? Forces and the Laws of Motion Solution ml = 170 kg mh = 75kg a = 10.0m/s2 Flion Fhuman mliona mhumana (170kg)(10.0m / s 2 ) (75kg)(10.0m / s 2 ) 950 N Forces and the Laws of Motion Homework Problems • Pages 151 – 152 – 10 (1210N 62o above the 1520N Force) – 12 (4N, 3N) – 23 (a, 6.00s b, 72.0m c, 63.6m/s) – 25 (a, 2.3m b, 1.8m) Forces and the Laws of Motion Types of Forces Weight (Fg) • Long Range Force Exerted by Gravity on the Object • Toward the Center of the Earth Normal (FN) • Exerted by Surface on the Object • Perpendicular to Surface Forces and the Laws of Motion The Normal Force The normal force is the perpendicular contact force exerted by a surface on another object. The normal force is important when calculating resistance. Forces and the Laws of Motion Types of Forces Friction (Ff) • Opposes Horizontal Motion • Parallel to Surface Tension (FT) • Pull or Push Exerted by Secondary Object • Parallel to Secondary Object Forces and the Laws of Motion Friction Drag (Fdrag) • Friction of Medium on an Object Terminal Velocity • Fdrag = Fg Forces and the Laws of Motion Forces of Ropes and Strings The force exerted by a string or rope is called tension. At any point in a rope, the tension forces are pulling equally in both directions. Forces and the Laws of Motion Mass & Weight On Earth • Fg = mg – g is the acceleration of Gravity (9.8 m/s2) • Mass = Weight? Forces and the Laws of Motion Apparent Weight Fg +/- Any Other Forces Weightlessness Apparent Weight = 0 Elevator Example... Forces and the Laws of Motion Static and Kinetic Friction Kinetic friction Exerted on one surface by another when the two surfaces rub against each other because one or both of them are moving. Static friction Exerted on one surface by another when there is no motion between the two surfaces. Forces and the Laws of Motion Static and Kinetic Friction You might push harder and harder, as shown in the figure below, but if the couch still does not move, the force of friction must be getting larger. This is because the static friction force acts in response to other forces. Forces and the Laws of Motion Static and Kinetic Friction Push hard enough and the couch will begin to move. There is a limit to how large the static friction force can be. Once your force is greater than this maximum static friction, the couch begins moving and kinetic friction begins to act on it instead of static friction. Forces and the Laws of Motion Static and Kinetic Friction Frictional force depends on the materials that the surfaces are made of. The normal force between the two objects also matters. The harder one object is pushed against the other, the greater the force of friction that results. Forces and the Laws of Motion Static and Kinetic Friction Forces and the Laws of Motion Static and Kinetic Friction The slope of this line, μk, is called the coefficient of kinetic friction between the two surfaces and relates the frictional force to the normal force, as shown below. Kinetic Friction Force f k k FN Forces and the Laws of Motion Static and Kinetic Friction The static friction force is less than or equal to the product of the coefficient of the static friction and the normal force. Static Friction Force f s s FN Forces and the Laws of Motion Static and Kinetic Friction The forces themselves, fs and FN, are at right angles to each other. Although all the listed coefficients are less than 1.0, this does not mean that they must always be less than 1.0. Forces and the Laws of Motion Force… • Is Not Transferred to the Object • Is Not Needed to Keep an Object Moving • Is Not Related to Inertia Forces and the Laws of Motion Problem If you use a horizontal force of 30.0N to slide a 12.0kg wooden crate across a floor at a constant velocity, what is the coefficient of kinetic friction between the crate and the floor? Forces and the Laws of Motion Solution fk = 30.0N m = 12.0kg f k k FN fk k FN fk fk 30.0 N k 0.26 2 FN mg (12.0kg)(9.8m / s ) Forces and the Laws of Motion Problem A force of 40.0N accelerates a 5.0kg block at 6.0 m/s2 along a horizontal surface. How large is the frictional force? Forces and the Laws of Motion Solution Fapplied = 40.0N m = 5.0kg a = 6.0m/s2 Facc Fapplied f k f k Fapplied Facc f k 40.0 N (5.0kg)(6.0m / s ) 10.0 N 2 Forces and the Laws of Motion Problem A force of 40.0N accelerates a 5.0kg block at 6.0 m/s2 along a horizontal surface. What is the coefficient of friction? Forces and the Laws of Motion f k k FN Solution Fapplied = 40.0N m = 5.0kg a = 6.0m/s2 fk fk k FN mg 10.0 N k 0 . 20 2 (5.0kg)(9.8m / s ) Forces and the Laws of Motion Problem You are driving a 2500.0kg car at a constant speed of 14.0m/s along a wet, but straight, level road. As you approach an intersection, the traffic light turns red. You slam on the brakes. The car’s wheels lock, the tires begin skidding, and the car slides to a halt in a distance of 25.0m. What is the coefficient of kinetic friction between your tires and the wet road? Forces and the Laws of Motion Solution d = 25.0m m = 2500.0kg vi = 14.0m/s vf = 0m/s 2 f k k FN ma m(v f vi ) 2 k mg 2 2d 2 vi (14.0m / s) k 0 . 40 2 2dg 2(25.0m)(9.8m / s ) Forces and the Laws of Motion Problem A street lamp weighs 150N. It is supported by two wires that form an angle of 120.0° with each other. The tensions in the wires are equal. What is the tension in each wire supporting the street lamp? Forces and the Laws of Motion Solution W = 150.0N q = 120o ? Fg 2T sin q T Fg 2 sin q 150 N T 150 N o 2(sin 30.0 ) Forces and the Laws of Motion Homework Problems • Pages 153 – 154 – 38 (0.436) – 41 (1.4m/s2 down the aisle) – 42 (1.0m/s2) – 43 (15.9N)