Download Checking for normality for a random sample. • Suppose that (X 1

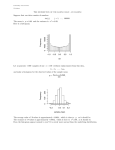
Checking for normality for a random sample.
• Suppose that (X1 , . . . , Xn ) is a random sample. We may check whether
the sample is from a normal distribution using a histogram.
• R codes for checking normality using a histogram (data = x)
## Draw a normalized histogram of x using Scott’s rule
c <- (24*sqrt(pi))^(1/3);s <- sd(x)
# s: sample standard deviation
n <-length(x)
k <- ceiling((max(x)-min(x))/(c*s*n^(-1/3)))
# k: number of classes
w <- (max(x)-min(x))/k
# w: class width
brks <- seq(min(x), by=w, length.out=(k+1))
# brks: class limits
hist(x, breaks=brks, include.lowest=TRUE, right=T, freq=F) # freq=F: do normalization
x1 <- seq(min(x), max(x), 0.01)
lines(x1, dnorm(x1, mean=mean(x), sd=sd(x)), col=2) # dnorm: normal density
• Example 1. Download the data file
http://www3.nccu.edu.tw/~tmhuang/teaching/statistics/data/test.txt
and then check the normality for the second column using a normalized
histogram.
Save the data file ”test.txt” in C:\temp. Use
y <- read.table("C:\\temp\\test.txt", sep=",")
x <- y[,2]
to read the data into R and store the second column in the vector x. The
histogram and the normal density can be drawn using the above codes.
• Example 2. Generate a random sample of size 3000 from N (0, 4) and
then check its normality using a normalized histogram.
To generate x: a random sample of size 3000 from N (0, 4), use
x <- rnorm(3000, mean=0, sd=sqrt(4))
1
The histogram and the normal density can be drawn using the above
codes.
• Suppose that (X1 , . . . , Xn ) is a random sample. We may check whether
the sample is from a normal distribution using the Kolmogorov-Smirnov
test. The null hypothesis for the Kolmogorov-Smirnov test is that the
distribution of each Xi is equal to a specific distribution with CDF F .
The test is based on the statistic
max F̂ (x) − F (x) ,
x
where
n
F̂ (x) =
1X
I(−∞,x] (Xi )
n i=1
and
I(−∞,x] (Xi ) =
1
0
if Xi ≤ x;
if Xi > x.
• R command for Kolmogorov-Smirnov test: ks.test(x, F) gives the result of testing whether x is a random sample from a population with CDF
F.
– To test whether x is a random sample from N (m, v ), use the command
ks.test(x, pnorm, mean=m, sd=sqrt(v)).
• Example 3. Download the data file
http://www3.nccu.edu.tw/~tmhuang/teaching/statistics/data/test.txt
and then check the normality for the second column using KolmogorovSmirnov test.
Save the data file ”test.txt” in C:\temp.
y <- read.table("C:\\temp\\test.txt", sep=",")
x <- y[,2]
ks.test(x, pnorm, mean=mean(x), sd=sd(x))
The p-value is 0.9817, so we do not reject the hypothesis that the population distribution is normal.
2