Download Chapter 4 Probability and Sampling Distributions

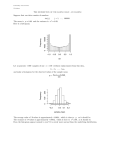
Reminders:




Parameter – number that describes the
population
Statistic – number that is computed
from the sample data
Mean of population = µ
Mean of sample = x
4.3 Sample Distributions
Statistical inference uses sample
data to draw conclusions about
the entire population
Statistical estimation and the law
of large numbers



As the number of observations drawn
increases, the mean x of the observed
values gets closer and closer to the
mean  of the population
Similar to flipping a coin “many times”
Foundation of gambling casinos and
insurance companies
Law of Large Numbers
Sampling distributions

the sampling
distribution of a
statistic is the
distribution
(histogram) of
values taken by the
statistic in all
possible samples of
the same size from
the same population
Hospital beds data






Make a histogram of the data & calculate the
population mean
Take 2 samples of ten and find the sample means
Make a histogram of all the sample means
Compare the population mean to the approximate
mean on the histogram
Take two more samples of ten and find the sample
means.
Make histogram of all sample means and compare to
population mean
Central limit theorem



As the sample size increases, the distribution
of x changes shape: it looks less like that of
the population and more like a normal
distribution (no matter what the population
curve looks like)
When the sample is large enough, the
distribution of x is very close to normal
Picture pg 245
Hospital beds data




Take 2 samples of 20 and find the sample
means
Make a histogram of all the sample means
Compare the population mean to the
approximate mean on the histogram
Compare the histogram made with 2 samples
of twenty to the histogram made with 2
samples of ten
When we choose many SRS’ s from a
population, the sampling distribution of
the sample means. . .



is centered at the mean of
the original population
is less spread out than the
distribution of individual
observations
The mean of the sampling
distribution of x is μ and
its standard deviation is 
n

Unbiased estimator – “correct on the
average in many samples”


because the mean of x is equal to μ, we
say that the statistic x is an unbiased
estimator of the parameter μ
The standard deviation of the
distribution of x gets smaller as we take
larger samples

Engineers are redesigning fighter jet ejection seats to
better accommodate women. In human engineering
and product design, it is often important to consider
people’s weights so that airplanes or elevators aren’t
overloaded, chairs don’t break, etc. Given that the
population of women has normally distributed
weights with a mean of 143 lb and a standard
deviation of 29 lb, find the probability that


If 1 woman is randomly selected, her weight is greater than
150 lb
If 36 different women are randomly selected, their mean
weight is greater than 150 lb
Interpretation


There is a 0.405 probability that a woman will
weigh more than 150 lb, but there is only a
0.0738 probability that 36 women will have a
mean weight of more than 150 lb.
It is much easier for an individual to deviate
from the mean than it is for a group of 36. A
single extreme weight among the 36 weights
will have reduced impact when it is averaged
in with the other weights.

IQ scores are normally distributed with
a mean of 100 and a standard deviation
of 15. If 25 people are randomly
selected for an IQ test, find the
probability that their mean IQ score is
between 95 and 105.