Download 235_lecture5_080212

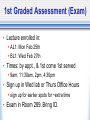
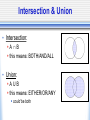
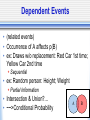
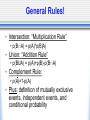
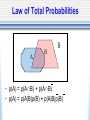
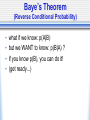
Psyc 235:
Introduction to Statistics
http://www.psych.uiuc.edu/~jrfinley/p235/
DON’T FORGET TO SIGN IN FOR CREDIT!
1st Graded Assessment (Exam)
• Lecture enrolled in:
 AL1: Mon Feb 25th
 BL1: Wed Feb 27th
• Times: by appt., & 1st come 1st served
 9am, 11:30am, 2pm, 4:30pm
• Sign up in Wed lab or Thurs Office Hours
 sign up for earlier spots for ~extra time
• Exam in Room 289. Bring ID.
1st Graded Assessment (Exam)
• ALEKS will be unavailable:
 AL1: 8am Mon - 11:59pm Wed
 BL1: 8am Wed - 11:59pm Fri
• Conflict/Makeup exams:
 must be within that window
 let us know ASAP (as in TODAY)
Probability: Multiple Events
• Mutually Exclusive Events
• Independent Events
• Dependent Events
 (Conditional Probability!)
Venn Diagrams
• Sample Space: set of all possible
outcomes of a random phenomenon
 big rectangle
 (defined by Researcher [e.g., YOU!])
• Event: subset of the possible outcomes
 circles (or whatever)
 (also defined by Researcher!)
• Populations...
Venn Diagrams
• Probability:
# outcomes in some event/subset
# outcomes in Sample Space
area of some event/subset
area of Sample Space
Intersection & Union
• Intersection:
AB
 this means: BOTH/AND/ALL
• Union:
AUB
 this means: EITHER/OR/ANY
 could be both
Mutually Exclusive Events
(a.k.a. “Disjoint”)
ex: 1 Coin toss: Heads;Tails
ex: 1 Student: Freshman;Senior
Intersection:
 p(AB)= 0
• Union:
 p(AUB)= p(A)+p(B)
A
•
•
•
•
B
Independent Events
• (unrelated events)
• ex: Multiple coin tosses: Heads 1st time;
Heads 2nd time
• ex: Draws w/ replacement: Red Car 1st
time; Yellow Car 2nd time
• Intersection:
 p(AB)= p(A)*p(B)
• Union:
 p(AUB)= p(A)+p(B) -p(AB)
A
B
Dependent Events
• (related events)
• Occurrence of A affects p(B)
• ex: Draws w/o replacement: Red Car 1st time;
Yellow Car 2nd time
 Sequential
• ex: Random person: Height; Weight
 Partial Information
• Intersection & Union?...
• ~~>Conditional Probability
A
B
Conditional Probability
• p(B|A)
• means: “The probability of B, GIVEN the
occurrence of A”
• No formula needed for the following:
• Mutually Exclusive Events:
 p(B|A)= 0
• Independent Events:
 p(B|A)= p(B)
Conditional Probability
• Formula:
p(B|A) =
p(BA)
p(A)
Conditional Probability
p(BA)
p(B|A)=
p(A)
• Dependent Events: Example
 100 people at party
 Could like: Beer, Wine, Both, or Neither
 p(Beer) =
 p(Wine) =
 p(BeerWine) =
 You see someone drinking Beer...
 p(Wine|Beer) =
Conditional Probability
p(BA)
p(B|A)=
p(A)
• Notes:
 The “GIVEN” becomes the denominator.
 ~like ‘zooming in’ on a subset
Back to Dependent Events:
Intersection & Union?
• Intersection:
 from
p(BA)
p(B|A)=
p(A)
 we get:
p(BA) = p(A)*p(B|A)
• Union:
 stays the same as for ind. events:
p(BUA) = p(A)+p(B)-p(BA)
General Rules!
• Intersection: “Multiplication Rule”
 p(BA) = p(A)*p(B|A)
• Union: “Addition Rule”
 p(BUA) = p(A)+p(B)-p(BA)
• Complement Rule:
 p(A)=1-p(A)
• Plus: definition of mutually exclusive
events, independent events, and
conditional probability
Tree Diagrams
• Independent Events
 all branches at a given level have same
probability
• Dependent Events
 probability of branch at a given level is
conditional on which branch of prior level
Law of Total Probabilities
A
B
_
B
• p(A) = p(AB) + p(AB)
• p(A) = p(A|B)p(B) + p(A|B)p(B)
Baye’s Theorem
(Reverse Conditional Probability)
•
•
•
•
what if we know: p(A|B)
but we WANT to know: p(B|A) ?
if you know p(B), you can do it!
(get ready...)
Baye’s Theorem
(Reverse Conditional Probability)
p(B|A) =
•
•
•
•
•
•
p(A|B)p(B)
p(A|B)p(B) + p(A|B)p(B)
Ex: HIV testing
A=test positive
B=person truly has HIV
Test’s Hit Rate: p(A|B)=.95
Test’s Correct Rejection Rate: p(A|B)=.95
But: say someone gets a positive test result...
false positive rate?
• say base rate of HIV: p(B)=.005
• calculate false positive rate: p(B|A)=...
Remember
• 1st Exam Feb 25/27
 Sign up for exam timeslots in lab Wed or
Office Hours Thurs
 (or also first-come-first-served on exam day)
• Sign in for lecture credit