Download Book 5

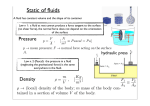
PHYSICS 125
Lecture Notes Book 5
Prepared by Kai Wong
Table of Contents
22. Fluid Pressure …………………………………………………………………. 2
23. Buoyancy ……………………………………………………………………….. 9
24. Temperature and Heat ………………………………………………………. 14
25. Kinetic Theory of Gases ……………………………………………………… 21
26. First Law of Thermodynamics ……………………………………………….. 25
27. Second Law of Thermodynamics ……………………………………………… 34
1
22. Fluid Pressure
Density The density of a substance is defined by

m
mass

V volume
It has the SI unit of kg/m3.
Sample values of densities:
 water  10 3 kg / m 3  1 g / cm 3
 steel  7.8  10 3 kg / m 3
 air  1.29 kg / m 3
Example: What is the radius of a sphere made of steel that has a mass of 100g?
m
0.1
Solution:
V 
 1.28 105 m3
 7800
From V 
4 3
r
3
r  3
3V
 1.45  10 2 m  1.45cm
4
Pressure When a force F acts perpendicularly on an area A , the pressure it exerts on
the surface is defined as
F
A
P
F
force

A area
The SI-unit of pressure is N/m2, which is written as Pa (pascal). Two other units are
1 ATM atmosphere  1.013  10 5 Pa  10 5 Pa
4.445 N
1 psi  1 lb / in 2 
 6890 Pa
2
1


m

 12  3.281 
1ATM  14.7 psi
2
Example: A woman weighing 700N stands on the heel of one high-heel shoe. The area of
the heel is 1cm2. How large is the pressure the heel exerts on the floor?


2
Solution: A  1cm 2  10 2 m  10 4 m 2
P
F 700
7  10 6
 4  7  10 6 Pa 
ATM  70 ATM
A 10
10 5
Fluid Pressure A fluid (gas or liquid) in a container exerts forces on the wall of the
container. It also exerts forces on the surface of a submerged object. In fact, even if the
submerged object is replaced by the fluid itself, the surface of the latter fluid still
experiences the same forces.
To define the pressure of a fluid at any point inside the fluid, we construct mentally a
small planar surface (say in the shape of a coin) of area A around that point. The fluid on
one side of the surface will push on the fluid on the other side with a force F, in a
direction perpendicular to the surface. The pressure is then calculated from P  F A . It
turns out as a fundamental property of a fluid that P is independent of the orientation of
the surface chosen.
F
A
Pascal Principle For an enclosed fluid not under the influence of gravity, the pressure is
the same everywhere in the fluid if it remains at rest, because a pressure difference would
set up motion. Therefore, if a change of pressure P occurs at one location, the same
change occurs everywhere. This is called Pascal principle.
Consider a fluid enclosed in a vessel with two pistons as shown. A piston is capable of
moving without leaking the fluid. If the forces on the pistons due to the fluid are denoted
3
by F1 and F2 , while the areas of the pistons are A1 and A2 , and if P is the pressure of the
fluid everywhere, we have
P
F1
A1
P
F2
A2

F1 F2

A1 A2
A2
A1
F1
F2
To push the left piston in, we need to apply a force equal to (actually slightly more than )
F1 . If the fluid is incompressible, its volume cannot change. The right piston is therefore
forced out with a force F2 . If A1 is less than A2 , then F2 is larger than F1 . In this way, a
small force is transmitted through the fluid and amplified to a lager force. This
phenomenon is exploited in a hydraulic lift:
F
A2
A1
W
F2
F1
A
F W

W  2 F  F if A2  A1
A1 A2
A1
Variation of pressure with height
Consider a fluid under the influence of gravity. First we show that the pressures at the
same level are equal. Label the points at the same level by 1 and 2, and construct
identical vertically oriented small areas around the points.
4
A
A
F1
F2
1
2
Consider the fluid inside a horizontal cylinder formed between the surfaces. Since this
fluid is in equilibrium, the sum of forces on it is zero. Balancing the push forces on either
sides of the two surfaces lead to
F1  F2
Or P1 A  P2 A
 P1  P2
Next consider two points so that point 1 is above point 2 by a height h. Construct
identical small horizontal surfaces at these points, and consider the condition of
equilibrium for the fluid inside a vertical cylinder between these surfaces. The upward
push on the bottom surface is now balancing the downward push on the top surface plus
the weight of the fluid column.
F1=P1A
h
W
F2=P2A
F2  F1  W
P2 A  P1 A  mg
Since the volume of the column is V  hA , we can write
5
m  V  hA
where  is the density of the fluid. Therefore
P2 A  P1 A  hAg
which simplifies to
P2  P1  gh
The pressure at 2 is higher than at the point 1 in order to support the weight of the fluid
above.
Combining the last result with the earlier one regarding pressures at the same elevation,
we see that the formula
P2  P1  gh
applies even if the point 2 is not directly below the point 1.
Example: What is the change in pressure in going down 10m of water in the ocean?
Solution: Choose the point 1 at the surface and point 2 at 10m below.
h  10m   10 3 kg / m 3 g  10m / s 2
P2  P1  gh  10 5 Pa  1 ATM
Example: What is the pressure 20m deep in the ocean?
Solution: P2  P1  gh  10 3  10  20  2  10 5 Pa  2 ATM
P2  P1  2  3 ATM
Toricelli’s experiment Fill a long glass tube with mercury and invert it in a trough of
mercury. The mercury in the tube will fall until its height is h . The value of h can be
calculated from the density of mercury and the pressure of the atmosphere.
1
h
2
6
Choose the point 1 to be at the top of the mercury column. The pressure
P1  0
because the space above it is vacuum.
Choose the point 2 to be at the bottom of the column. The pressure
where PA is atmospheric pressure, because pressure is the same at the
P2  PA
same level and the mercury in the trough is exposed to atmosphere.
Applying the formula for pressure variation of height, we find
PA  gh
where   13.6  10 3 kg / m 3 is the density of mercury.
The height of the column is therefore
PA
1.013  10 5
h

 0.76m  76cm
g 13.6  10 3  9.8
If water is used instead of mercury, h 
PA 1.013  10 5

 10m
g
10 3  9.8
Equalization of water level In a connected body of water exposed to the atmosphere,
the water surface is always at the same height. For example, in the odd-shaped vessel
shown, the points A,B and C in the fluid are chosen at the same height, and therefore
have the same pressure:
PA  PB  PC
The points A’, B’, and C’ at the water surface also have the same pressure, namely, the
atmospheric pressure:
PA  PB  PC   Patmosphere
Therefore the height h of the surface is the same, being given by
h
PA  PA PB  PB PC  PC 


g
g
g
7
B’
C’
A’
h
A
C
B
Pressure gauge A U-tube filled with mercury with one end exposed to the atmosphere
can be used to measure the pressure of a gas in a container connected to the other end of
the U-tube as shown.
PA
P
h
If P is the pressure of the gas, PA the atmospheric pressure, and h is the height of one
surface of the mercury column above the other, applying the formula for pressure
variation of height gives
P  PA  gh
The height h can therefore be used to measure the pressure difference P  PA , the amount
of pressure above atmospheric, which is known as the gauge pressure. We thus have
another unit of pressure
1 mm mercury  gh  13.6  10 3  9.8  10 3  133 Pa
1 ATM  760mm mercury
When the tire pressure is quoted as 32 psi, we should add the atmospheric pressure of
14.5psi to yield 45.5psi.for the absolute pressure.
8
23. Buoyancy
Buoyancy Force An object fully or partially submerged in a fluid under gravity
experiences an upward force due to the fluid. This force arises from the fact that the
pressure of the fluid is higher at the bottom of the object than at the top.
F1
A
1
f
h
2
F2
Consider a solid in the form of a rod of length h and cross-sectional area A, completely
submerged in a fluid of density  f . All faces of the solid are subject to compressive
pressure forces. The net upward component of theses forces is
B  F2  F1  P2 A  P1 A  P2  P1 A   f ghA   f gV  m f g  W f
Therefore,
Buoyancy force = weight of fluid displaced by the submerged volume of solid
This is known as Archimedes’ principle. It applies to objects of arbitrary shapes, as well
as to objects only partially submerged.
Apparent weight Consider an object completely submerged in a liquid and resting on
the bottom of the container. The forces on the object consist of its weight downward and
two upward forces: buoyancy and normal force.
9
B
FN
W
At equilibrium, B  FN  W  0
 FN  W  B
The normal force is the apparent weight, and is reduced from its true weight by an
amount equal to the buoyancy force.
B
T
W
Similarly, if the object is suspended by a string, the tension T in the string is less than the
weight, and is also a measure of apparent weight:
T W  B
The consideration from normal force applies also to partial submersion, as the following
example shows:
Example: A 20-kg piece of concrete is 80% submerged in water. What is the apparent
weight? (density of concrete = 2200 kg/m3)
10
Solution: First find buoyancy force B from Archimedes principle. For this we need the
volume submerged.
Volume of concrete block V 
3
m
 concrete

20
 9.1  10 3 m 3
2200
Vsubmerged  0.8V  7.3 10 m
From Archimedes principle,
B   water gVsubmerged  1000  9.8  7.3 10 3  72N
W  mg  20  9.8  196 N
FN  W  B  196  72  124 N (apparent weight)
3
Determination of density from apparent weight The weight of a solid with volume
V and density  solid is given by
W   solidVg
The buoyancy force on the same solid when it is completely submerged in water is given
accordingly to Archimedes principle by
B   waterVg
By definition,
the specific gravity S.G. of a substance = density of the substance /density of water
It follows from the above two relations that
S .G. of solid 
 solid  solidVg W


 water  waterVg B
Thus we can determine the specific gravity of the solid if we can measure the buoyancy
force. The latter can be determined from the apparent weight W a of the solid when it is
completely immersed in water using the equation
B  W  Wa
A balance scale can be used to measure the apparent weight of the solid while under
water in an arrangement as shown:
11
B
W
Wa
:
Example: The emperor’s crown weighed 2 lb in air and 1.8 lb under water. Is it made of
gold?
Solution: Weight of crown W  2 lb
Apparent weight in water Wa  1.8 lb
 Buoyancy force B  W  Wa  2.0  1.8  0.2 lb
W 2.0
S .G. of crown material 

 10
B 0.2
Density of crown material  solid  S .G.   water  10  10 3 kg / m 3  10 4 kg / m 3
Since the density of pure gold is  golkd  19,300kg / m3 , the emperor had been
cheated.
Floatation The criterion whether a solid will float or sink in a liquid is given by
Sink :  solid   liquid
Float :  solid   liquid
This can be derived as follows. Consider the solid to be completely immersed in the
liquid and not in contact with the bottom of the container.
B
V
W
Net upward force  B  W   liquidVsolid g   solidVsolid g   liquid   solid Vsolid g
12
The object will start to rise (float) if the net force is upward, which happens if
 liquid   solid . Otherwise, it moves downward, or sink. In the former case, the object will
rise until part of its volume protrudes into air, so that it is only partially submerged. The
buoyancy force is therefore reduced, and can balance the weight, as the following
example shows:
Example: What fraction of the volume of an iceberg is beneath water?
( (  ice  917kg / m 3 )
Solution:
B
W
At equilibrium, B  W

Vsubmerged

Or,  waterVsubmerged g   ICE Vice g
 ice
917

 0.917
 water 1000
Vice
 Tip of iceberg  8.3% of total volume.
Example: A raft floating on water has a bpttom that measures 2m 1m .w much does it
sink in level when a 30kg child steps on it?
Solution:
Without child, B  Wraft
With child, B   Wraft  Wchild
 Additional buoyancy force B  B  B  Wchild
From Archimedes principle, B   water Vsubmerged g
 Vsubmerged 
Wchild
m
30
 child 
 0.03m 3
 water g  water 1000
Since Vsubmerged  Ah
 h 
Vsubmerged
A

A  area ofbottom, b  change in water level
0.03
 0.015m  1.5cm
2 1
13
24. Temperature and Heat
Temperature Scales Most substances expand when heated, and contract when cooled.
The amount of expansion or contraction can be used to measure temperature.
In a mercury thermometer, mercury is trapped in a glass container consisting of a bulb
connected to a thin tube. When the bulb is immersed in a mixture of ice and water, the
level of mercury in the tube is marked off and labeled 0°C. When it is immersed in a
mixture of steam and water, the corresponding mark is labeled 100°C. The reason for
choosing such mixtures to define 0°C and 100°C is because the temperatures of these
mixtures are fairly constant, not being influenced much by the heat absorbed from or
released to the environment. The length between these marks is then divided into 100
equal parts. When the bulb is in contact with the object whose temperature is being
measured, the temperature is indicated by the level of mercury. In this way, the
centigrade scale, or Celsius scale, is defined. It is a property of mercury (as well as many
other liquids) that the same reading is obtained for thermometers thus constructed.
100 ºC
212 ºF
steam+water
TC ºC
TFºF
0 ºC
32 ºF ice+water
In the Fahrenheit scale, the marks for ice-water and steam-water mixtures are labeled
32°F and 212°F respectively, and the length between the marks is divided into 180 equal
parts. The notations for differences of temperatures in the two scales are C° and F°. We
have
1C 
1`80  9 
F  F
100
5
If TC and TF denote the temperatures in the Celsius and the Fahrenheit scales, we have,
from the construction of the scales,
TC  0 TF  32

100
180
14
9
This can be solved to yield either TF  32  TC
5
5
Or TC  TF  32 
9
The constant volume gas thermometer relies on the increase of gas pressure with
temperature for temperature measurement. It consists of a gas trapped inside a glass bulb
connected to a U-tube filled with mercury. The U-tube is open to the atmosphere on the
other end, and is partly made from rubber tubing so that it can be raised or lower to
ensure that the volume of the trapped gas remains constant as the bulb is introduced into
various temperature environments. The height of the mercury column is a measure of the
gauge pressure of the gas.
PA
P
P=PA+ρgh
h
Experiments show that
(1) A plot of P versus TC (temperature in Celsius) is a straight line.
(2) Extrapolating the straight line to P=0 results in the same temperature of -273 ºC
independently of
(a) the amount of the trapped gas
(b) the nature of the trapped gas
P
-273ºC
TC
TC+273
TC (ºC)
If we define temperature in Kelvin scale TK (K ) by
TK  TC  273
15
(Note that we do not use the degree notation with K) , then the plots of P versus TK are
straight lines passing through the origin:
P
0K
TK(K)
As a result, P is proportional to TK : P  TK , with the proportionality constant
depending on the nature and the amount of the trapped gas. The Kelvin scale not only
simplifies formulas for the properties of gases, it turns out also to have an absolute
meaning from thermodynamics. For this reason, it is also called the absolute
temperature, No object can have negative temperature in the Kelvin scale,
Heat Capacity To raise the temperature of an object, we can bring it in contact with
another with higher temperature. For example, water in a pot is heated through contact
with the hot gas from a gas stove. The influx of heat causes the temperature to go up,
while an outflux of heat causes it to go down. In the past, people thought that heat is a
substance, flowing from high temperature to low temperature like water flowing from
high to low elevations. The increase of temperature of an object is proportional to the
quantity of heat absorbed by the object, while the decrease of temperature is proportional
to the quantity of heat released. This relation is expressed by the equation
Q  CT
T  T f  Ti
where Q is positive if heat is absorbed and negative if heat is released. The constant of
proportionality C is called the heat capacity of the object. Objects with higher heat
capacity require more heat to have their temperature raised by the same amount.
Conversely, for the same amount of heat absorbed, such objects will experience less
increase in temperature.
16
ΔT
Q
For objects made of pure substances, the heat capacity is expected to be proportional to
the mass. If the mass of the object is m , the relation between heat absorbed and
temperature rise is written as
Q  mcT
where the quantity c (lower case) is called the specific heat capacity, or just specific
heat, of the pure substance.
In the caloric theory, heat is measured in a unit called the calorie. This is defined to be
the quantity of heat required to raise the temperature of one gram of water by 1 C  .
Substituting into the relation between Q and T :
1cal  1g  c  1C 
Therefore, the specific heat of water is
c water  1 cal / g  C 
Calorimetry The caloric theory also postulates that heat is indestructible so that, for
instance, the heat released by an object must be equal to the heat absorbed by all others
with which it comes into contact. This can be expressed by the equation
Q  0
where the summation is over all objects in thermal contact with each other, and Q is the
heat absorbed by each, with a negative Q meaning heat released. In terms of specific
heat and temperature change for each object, assumed to be made of pure substance,
 mcT  0
This can form the basis of determining specific heat as the following example shows:
17
Example: A 50g sample of aluminum is heated to 100°C in a pot of boiling water. It is
then introduced into 20g of water initially at 25°C in a well insulated container. The final
temperature is 51°C. Determine the specific heat of aluminum.
Solution: The equation  mcT  0 becomes
50c Al 51  100  20cwater 51  25  0
Using c water  1cal / g  C  , this becomes
 2450c Al  520  0
so that c Al 
520
 0.21cal / g  C 
2450
Such experimental procedures that account for heat flows using apparatus that minimize
heat leak to the environment form the basis of calorimetry.
The Mechanical Equivalent of Heat The temperature of an object can also be raised by
rubbing. The force doing the rubbing does work against friction, and its effect on the
object is equivalent to the absorption of heat. It is found that a given amount of work is
always converted to the same amount of heat. Joule’s experiment demonstrates this and
establishes how many Joules of work is equivalent to 1 calorie.
The apparatus used by Joule is as shown, consisting of paddles that can be set to rotate by
a falling weight, thus churning the water in the thermally insulated container. The
equivalent heat in calorie absorbed by the water can be calculated from a reading of the
rise in temperature and the mass of the water. The corresponding amount of work
measured in Joule is obtained from the height through which the hanging weight falls.
In this way, it was found that
1 calorie is equivalent to 4.186 J
18
which is called the mechanical equivalent of heat. Since work and energy have the same
unit, we can regard heat as just a flow of energy, or energy in transit. Objects heat up
when they absorb energy.
Converting from calorie to J and gram to kilogram, the specific heat of water can be
expressed as
c water  1cal / g  C   4.186 J / 10 3 kg  C   4186 J / kg  C 
Example: What is the final temperature when a 75g silver ring at 100°C is dropped into a
cup containing 10cc water at 20°C? (The specific heat of silver is 235J / kg  C  )
Solution: The mass of 1cc of water is 1g. Let T f be the final temperature of the water and
ring, the equation
 mcT  0
becomes 0.075  235  T f  100  0.010  4186  T f  20  0
17.6T f  1783  41.86T f  837  0
Tf 
1783  837
 43.7  C
17.6  41.9
Latent Heat All substances can exist in the three phases of solid, liquid, and vapor,
depending on the temperature (and also the external pressure). The transformation from
solid to liquid is known as melting, and the reverse freezing. The transformation from
liquid to vapor is known as vaporization, and the reverse condensation. For a given
pressure, there is a unique temperature at which the solid and the liquid phase can coexist. This temperature is known as the melting point. Similarly, the temperature at which
liquid and gas can coexist is known as the boiling point. During phase transition, the
temperature remains at either the melting or the boiling point, although heat is absorbed
or released. Heat is absorbed by a substance undergoing melting and vaporization, and is
released to the environment during freezing and condensation. The amount of heat
absorbed or released is proportional to the mass of the substance. Latent heat of
vaporization is the amount of heat absorbed by unit mass (1 kg in SI unit) of a substance
being transformed from the liquid to the vapor phase. The same amount of heat is
released when the substance condenses. Latent heat of fusion is the heat absorbed by
unit mass of the substance being transformed from solid to liquid phase, and is released
during freezing. These are known as latent heats because there is no change of
temperature involved. The following values apply to water:
Latent heat of fusion LF  80 cal / g  3.35  10 5 J / kg
Latent heat of vaporization Lv  538 cal / g  C   2.26  10 6 J / kg  C 
19
The rather large value of the latter is responsible for the phenomenon of scorching. The
skin in contact with steam absorbs a huge amount of energy from the condensation of
steam into water.
If m is the mass of a substance that has undergone phase change, and L is the
corresponding latent heat, the amount of heat absorbed or released is given by
Q  mL
The following plot of temperature against heat absorbed pertains to 1 g of the water
substance starting as 10°C subfreeze ice.
T(°C)
100°C
water+steam
steam
water
0°C
80cal
536cal
Q(cal)
Ice+water
-10°C
ice
Example: How much ice is melted when 20 kg of ice 0°C absorbs 106 J of heat?
Solution: Amount of heat to melt all 20 kg of ice is
Q  mL fusion  20  3.35 105  6.7 106 J
which is more than 106 J. Therefore, the ice is not completely melted.
10 6
 3 kg
The amount melted =
3.35  10 5
Example: If in the previous example, the amount of heat absorbed is 107 J, what is the
final temperature?
Solution: Since 107J is more than 6.7  10 6 J , the ice has completely melted. The heat
anbsorbed goes to both melting the ice and heating up the resulting water. Fron
Q  mL  mcT
Q  mL 10 7  6.7  10 6
T 

 39C 
mc
20  4186
Therefore the final temperature is 39°C.
20
25. Kinetic Theory of Gases
Derivation of Ideal Gas Law
The ideal gas law can be written in another form if we replace the mole number n by the
relation
n  N NA
where N is the number of molecules and N A is Avogadro’s number. The result is
PV  NkT
where
k
R
 1.38  10 23 J / K
NA
can be regarded as the ideal gas constant per molecule, and is known as the Boltzmann
constant.
The theory of gases has been developed as a phenomenological theory in which
concepts and relationships are extracted from experiments. For example, temperature is
such a concept. A more fundamental theory known as the kinetic theory is able to explain
the ideal gas law in terms of purely mechanical concepts such as forces and Newton’s
laws of motion. In this theory, the gas is made up of a collection of molecules which are
constantly moving inside the container. The number of molecules is very large. When a
molecule strikes the wall of the container, it bounces back just like a tennis ball bouncing
back from the ground it hits. In so doing, the molecule delivers a force on the wall, and
this the origin of pressure of the gas.
To obtain a quantitative relation for the pressure, we consider for simplicity a cubical
volume of side L containing N molecules of the same mass m . The volume is V  L3 .
We assume the molecules are equally divided among six populations, traveling
respectively with the same speed v in the  x directions,  y directions, and
 z directions. We focus our attention on an area A on one face of the cube, and ask
how many molecules will hit the face in a time interval t . These would be molecules
moving toward that face and within the distance vt from the face. Such molecules are
shown in red in the figure. (Molecules further away from the face shown in black could
not reach the face in the interval t ) They are all in a volume vtA .
21
vt
A
Since the number density of molecules is N V , the number of molecules in this volume
and traveling toward the face is therefore
1N
vtA (=number of molecules striking area A in time t )
6V
Assuming elastic collision with the wall, each molecule bounces back with the same
speed but in the opposite direction, and so
momentum loss in each collision = 2mv
The loss of momentum of the colliding molecules is
p 
1N
1N
vtA2mv 
mv2 At
6V
3V
Force on the colliding molecules is
p 1 N

mv2 A
t 3 V
which, by Newton’s third law, is also equal to the force on the face of the cube. The
pressure on the face is therefore
P
F 1N
2N

mv2 
K
A 3V
3V
where K  mv2 2 is the kinetic energy of the molecule. We thus have
PV 
2
NK
3
If we compare this relation with the ideal gas law, we see that they are the same if we
make the identification
22
K
3
kT
2
Thus, the temperature of an ideal gas is related to the kinetic energy of the individual
molecules, and we have found a mechanical explanation of the ideal gas law.
In a more complete version of kinetic energy, the molecules do not all move with the
same speed, and certainly do not move in only six directions. But the average kinetic
energy K is still given by
K 
1 2 3
mv  kT
2
2
From this we find the root mean squared (rms) velocity
vrms  v 2 
3kT
m
as the typical speed of a molecule. Thus the rms velocity increases with temperature, and
is smaller for heavier molecules.
Example: Find the rms velocity of oxygen molecules at 20ºC.
Solution: The molecular weight of oxygen gas O2  is 2 16  32
 m  32  1.66  1027 kg
vrms 
3kT

m
T  273  20  293K
3  1.38  1023  293
 478m / s
32  1.66  10 27
Under ordinary circumstances, gas molecules traveling at such high speed are
continuously bumping into each other and change course. They follow zigzag paths with
tiny straight sections called the mean free path, which is the path length between
successive collisions. The time between collisions is very short.
Internal Energy
Multiplying the average kinetic energy of a molecule by the total number of molecules,
we obtain the total kinetic energy of the gas:
U  NK 
3
3
NkT  nRT (monatomic gases)
2
2
This is the internal energy of a monatomic gas, such as helium, neon, etc., whose
molecule consists of a single atom. For diatomic gases, such as oxygen O2  , nitrogen
23
N2  , the molecule is like a short bar, and can tumble as it travels. There is additional
kinetic energy associated with the tumbling motion, which is describable as rotation. For
such gases, the internal energy is given by
U 
5
nRT
2
(diatomic gases)
In general, the internal energy of a macroscopic body is the sum total of the kinetic
energy and the potential energy of the interaction between the molecules. For an ideal
gas, the molecules are free from interaction between each other. There is therefore no
contribution from the potential energy of interaction to the internal energy. As the
temperature is lowered, the speed of the molecules can no longer overwhelm the
influence of the force of attraction between the molecules. The gas will no longer behave
as an ideal gas, and its internal energy will have significant contribution from the intermolecular potential energy. Thus, while a mass of steam at high temperature can be
considered as an ideal gas, and has the aforementioned expression for internal energy,
when it condenses to water, that expression can no longer apply. The internal energy of
the water has a large influence from the potential associated with the cohesive force
between its molecules.
Using the ideal gas equation PV  nRT , an alternative expression for the internal energy
is
3
 2 PV
U 
 5 PV
 2
monatomic
diatomic 
Example: Find the internal energy of 1L of oxygen at STP.
Solution:
Method 1: Since at STP, the volume occupied by one mole of an ideal gas is 22.4L, the
number of moles in 1L volume is
n
1
 0.045
22.4
Also, T  273K .
5
5
 U  nRT   0.045  8.31  273  255 J
2
2
Method 2: P  1ATM  1.01 105 Pa V  1L  103 m3
U 
5
PV  253 J
2
24
26. First Law of Thermodynamics
A thermodynamic system is composed of one or more macroscopic objects, and as such
is very general. It can be a gas in a container, a glass of water, the chair you are sitting on,
or even a human being. The only requirement is that a large number of molecules are
present in the system, which is what we mean by macroscopic.
When two systems of different temperatures are brought into contact with each other,
heat will flow from one to the other, and will cease only when the two reach the same
temperature. It will take some time before this happens. In this case, we say that the two
systems are in thermal equilibrium. Thus, the temperature of a system indicates whether
or not the system can be in thermal equilibrium with another system. The zeroth law of
thermodynamics states that two systems are thermal equilibrium when they have the
same temperature.
We also introduce the concept of a system itself in thermodynamic equilibrium. This
means that the various parts of the system are in mechanical as well as thermal
equilibrium. In particular, the temperature of a system in thermodynamic equilibrium is
the same everywhere in the system. In this regard, the human being is not in
thermodynamic equilibrium, because different parts of the body have different
temperature. If a system is isolated so that it does not exchange heat and does not interact
with its environment, it would reach thermodynamics equilibrium after being disturbed.
The time for this to happen is called the relaxation time. The state of a system in
thermodynamic equilibrium is characterized by a number of variables called the state
variables. For a gas, its pressure, volume, and temperature are examples of state
variables.
Experiments showed that a system in thermodynamic equilibrium has a state variable
called its internal energy. The internal energy is composed of the microscopic kinetic
energy of the molecules and the potential energy of interaction among the molecules. For
a system consisting of a fixed number of molecules, the internal energy can be changed in
two ways:
(1) flow of heat into and out of the system
(2) work done on or by the system
Clearly, the internal energy increases if it absorbs heat, and decreases if it releases heat.
When the system does work to the environment, such as happens when the hot gas inside
a cylinder in an internal combustion engine expands and pushes the piston, or when a
person pushes on the paddles while riding an exercise bike, the internal energy decreases.
In this case, we say that work is done by the system. Work can also be done on the
system. If the system is a glass of water, work is done on it if the water is stirred. Work is
also done on the gas inside a container if the container is squeezed so that its volume is
reduced.
Let
25
U = internal energy of the system
Q = heat absorbed by the system
W = work done by the system
with the understanding that a negative value of Q means heat is released, and a negative
value of W means that work is done on the system, the change of internal energy is given
by
U  Q  W
This is known as the first law of thermodynamics, and can be pictorially represented:
ΔU
W
Q
It is interesting to compare the first law of thermodynamics with the work energy
theorem in mechanics. The latter states that the total work done by the all the forces
acting on an object is equal to the change of kinetic energy, and is written as:
K   W
The total work done by the forces can be regarded as the work done on the object. The
work done by the object is therefore the negative of  W . Thus
K   work done by the object
and is similar to the first law of thermodynamics except there is no flow of heat in
mechanics.
Example: A sample of two moles of an ideal monatomic gas undergoes a change during
which it receives 240J of heat and 60J of work is done on it. Find the change in
temperature.
Solution: Heat received by the system Q  240 J
Work done by the system W  60 J
Change of internal energy U  Q  W  240  60  300 J
26
3
nRT for monatomic gases,
2
3
2 U 2
300
U  nRT
 T 
 
 12 K
2
3 nR 3 2  8.31
Using U 
P-V Diagram of An Ideal Gas
The state variables P, V , T and n of a gas in thermodynamic equilibrium are not
independent. For an ideal gas, they are related by the ideal gas law. Let’s write the ideal
gas law in the form
P
nRT
V
and plot P against V at a fixed temperature. We obtain a curve that is a hyperbola::
P
V
If we increase the temperature and make another plot, we obtain another hyperbola lying
above the original one. If we decrease the temperature, we obtain a hyperbola that lies
below. In this way, we construct a family of hyperbolas. On each hyperbola, the
temperature is the same, but pressure and volume can change. Each hyperbola is called an
isotherm.
In the P-V diagram for a fixed mass of gas, each point represents a state in
thermodynamic equilibrium. A thermodynamic process is a course of events involving
change of states. If the process is slow enough so that the system has time to relax to
thermodynamic equilibrium as the change progresses, the process is called quasi-static.
Such process can be represented by a path in the P-V diagram, as illustrated by the red
curve in the following diagram, which also shows a family of isotherms.
27
P
2
1
V
Work done by a gas
Consider a gas inside a cylinder with cross-section area A fitted with a piston.
Δx
P
A
Let P be the pressure of the gas. Then the force acting on the piston due to the gas is
F  PA
Suppose the piston moves through an infinitesimally small distance x . During this
displacement of the piston, the volume change of the gas is small, and its pressure is
essentially unchanged. The work done by the gas is therefore
W  Fx  PAx  PV
where we have used the fact that V  Ax is the change in volume of the gas. It turns
out that the above formula for the work done by a gas during an infinitesimal change of
volume is applicable to any shape of the container. The work by the gas is positive when
the gas expands, and negative when the gas contracts.
When the volume change is not small, the pressure of the gas changes in the course of the
volume change, and the above formula no longer applies. In this case, the work depends
on the particular process during which the volume changes. It can be computed by
dividing the overall volume change into many small parts, for which the incremental
work can be computed by the above formula, and summing the contributions from these
infinitesimal works:
W   PV
In the P-V diagram, the product PV is equal to the area of the rectangle as shown. In
the limit when V is very small, the total work is therefore equal to the area underneath
the P-V curve for the process from the initial volume V1 to the final volume V 2 . It should
28
be noted that if V1 is less than V 2 , the work done by the gas is the negative of the area
underneath the P-V curve.
P
W=A
A
V1
P
V2
W  A
V1
ΔV
V2
V
A
V2
22
V1
Thermodyanamic Processes of ideal gas
(1) Isothermal Process
During an isothermal expansion of an ideal gas, the temperature is kept constant at T,
while the volume expands from V1 to V 2 . The path of the process in the P-V diagram is
part of the isotherm at the temperature T. The work done by the gas, which is equal to the
area underneath the P-V curve, can be obtained by calculus. The result is
W  nRT ln
V2
V1
V1
V2
The same formula applies to isothermal contraction, for which V1 is larger than V 2 , and
the work by the gas turns out to be negative.
Since the internal energy of an ideal gas depends only on n and T , it does not change
during an isothermal process:
U  0
29
Using the first law of thermodynamics, U  Q  W , the heat absorbed by the gas is
Q W
In this case, we can say that the expanding gas draws on the heat it absorbs from its
environment to do work.
Example: How much heat is released when 3 moles of an ideal gas is compressed
isothermally at the temperature 50ºC so that its volume is reduced by a factor of ten?
Solution: n  3 T  273  50  323K V2 V1  1 10  0.1
W  3  8.31 323  n0.1J   3  8.31 323   2.30  1.85 10 4 J
Since U  0 , the heat absorbed is Q  W . Therefoe heat released is 1.85×104 J.
(2) Isobaric Process
In an isobaric expansion, an ideal gas changes its volume from V1 to V 2 while maintaining
the pressure at P. The P-V diagram is a horizontal straight line, so that the work done is
W  PV2  V1   PV
if we define V  V2  V1 .
P
V
V1
V2
The temperature changes because the path on the P-V
diagram brings the state
from one isotherm to another. Writing the ideal gas law in the form
T
PV
nR
the temperatrure change is
P V
T 
nR
If the gas is monatomic, its internal energy will change by the amount
U 
3
nRT
2
and it will absorb an amount of heat according to the first law of thermodynamics by
30
Q  U  PV 
3
5
nRT  nRT  nRT
2
2
Therefore, the molar heat capacity at constant pressure is, by definition,
cp 
Q
5
 R
nT 2
J / mol  K
Replacing 3 2 in the formula for U by 5 2 , the same derivation shows that for
diatomic gases,
cp 
7
R
2
J / mol  K
Example: Find the change in internal energy when 1 kg of water at 100ºC is converted
into steam at the same temperature under a pressure of 1 atmosphere, assuming that the
steam can be considered an ideal gas. (The heat of vaporisation of water is 2.26×106J)
Solution: The process is isobaric. The initial volume is essentially zero considering the
much larger volume of the steam generated. The work done by the system is therefore
W  PV  nRT
where we have used the ideal gas law in the last equality. Since the molecular weight of
water (H2O) is 18, the number of moles is
n
1000
 55.6
18
and the temperature is 373K.
W  55.6  8.31 373  1.7 10 5 J
The change of internal energy is
U  Q  W  2.26 10 6  1.7 10 5  2.110 6 J
almost all the heat absorbed goes to increase the internal energy
(3) Isochoric Process
31
In an isochoric process, the temperature of a ideal gas changes from T1 to T2 with the
volume held constant at V . The process is represented by a vertical line segment in the
P-V diagram.
P
V
V
In this case, the work done by the gas is
W 0
so that from the first law, the heat absorbed is equal to the change of internal energy
Q  U
The latter can be computed from
U 
3
nRT
2
for monatomic gas. Hence the molar heat capacity at constant volume is
cV 
Q
3
 R
nT 2
for a monatomic gas. For a diatomic ideal gas, the result is
cV 
Q
5
 R
nT 2
The molar heat capacity at constant pressure is higher than at constant volume, because in
the former case, the heat absorbed is used up to do work against the environment in
addition to increasing the internal energy.
Example: Find the specific heat capacity of oxygen at constant pressure and constant
volume.
Solution: Since the molecular weight of oxygen (O2) is 32, the number of of moles in 1
kg of oxygen is n  1000 32  31.25 . The two specific heat capacities are
5
cV  31.25   8.31  649 J / kg  C 
2
7
c P  31.25   8.31  909 J / kg  C
2
32
(4) Adiabatic Process
This is a process in which expansion or compression takes place without heat exchamge
with the environment. It can be arranged if the gas is contained in a thermally insulated
vessel whose volume can change. It also occurs in an unsilated environment if the
compression or expansion is fast enough so that there is no time for heat exchange to take
place to a significant degree.
For an idiabatic process,
Q0
so that
U  W
In an adiabatic expansion, the gas does work against the environment, so that W is
positive. It therefore loses internal energy and cools down. Conversely, in an adiabatic
compression, work is done on the gas by the environment, so that W is negative, resulting
in an increase of internal energy and hence temperature. The Santa Ana conidtion results
from rapid rise of pressure and the consequent adiabatic conmpression in the atmosphere.
If the volume expands from V1 to V 2 adiabatically, both pressure and temperature will
change. The final state will lie on an isotherm lower than that of the initial state. The path
of an adiabatic process is steeper than an isotherm as shwon in the figure. It can been
shown that in the pressure and volume are related in this case by
P1V 1  P2V2
P
V
where  is the ratio of specific heat at constant pressure and constant volume:

c P 5 3

cV 7 5
monatomic
diatomic
33
27. The Second Law of Thermodynamics
Irreversible Transformations
Many changes or processes in mechanics are reversible. If two billiard balls collide and
fly apart, it is possible to reverse the paths and velocities of the balls after the collision
and recover their paths and velocities before the collisions. A planet may go around the
sun in one direction in its orbit. But the motion in which it traverses the same orbit but in
the opposite direction is perfectly acceptable. Watching a movie made of such processes,
you cannot tell whether the movie is being run forward or backward.
However, for changes involving macroscopic objects, many are irreversible. A
transformation in a thermodynamic system is called irreversible if the original state
cannot be recovered in such a way that no other changes occur anywhere else. The
following are three examples:
1. The heating of an object by friction. To make this precise, consider Joule’s
experiment in which water is heated up by a falling weight driving paddles to stir
up the water. It is impossible to make the water cool back to the original
temperature and raise the weight back to its original height, with nothing else
happening in the rest of the environment. Since in the Joule experiment, the work
done by gravity on the weight is completely transformed into heat, the reverse
change of transformation of heat completely into work is impossible.
2. The transfer of heat from a hot object to a cold object. In this case, it is not
just impossible for the heat to flow directly back through thermal contact, which
is obvious because by definition heat flows from high to low temperatures. In
fact, no means can be found to take the heat from the cold object and deliver it to
the hot one, with no other change in the environment.
3. The expansion of an ideal gas in a fixed volume container that allows no heat
flow in and out. Imagine the container to be partitioned at the beginning, with the
gas occupying one side and vacuum the other side. On opening the partition, the
gas expands to occupy the full volume of the container. On the other hand, once
filling up the container, the gas never by itself shrinks back to its original volume,
leaving vacuum behind. We note that the temperature of the gas has not changed
when it expands to fill the vacuum, because it does no work in expanding into a
vacuum, and there is no exchange of heat with outside. Consequently there is no
change in its internal energy according to the first law of thermodynamics. This
means no change of temperature because the internal energy of an ideal gas
depends only on temperature but not pressure or volume. It would be possible to
restore the gas to its original state by compressing it isothermally. However, this
entails doing work on the gas, which is achieved, for example, by a weight falling.
There is then a change in the environment, so that the imagined process does not
qualify for the consideration of irreversible transformation.
34
Reversible Transformations
On the other hand, there are transformations of thermodynamic systems that are
reversible. For example, the volume of a gas can be increased in a reversible
isothermal process. To arrange for this, we place an ideal gas in a cylinder that has a
piston on top and a bottom made of material that is perfectly heat conducting. The
bottom sits on a large object with a fixed temperature. The piston is raised slowly to
allow enough time for heat to flow from the large object so that the temperature of the
gas remains fixed at that of the reservoir. The infinitesimal changes in volume add up
to a sizable change. During the transformation, the state of the gas is described by its
pressure, temperature, and volume that obey the ideal gas law. The process itself can
be represented as a curve in the P-V diagram going from state A to B as shown:
P
A
B
V
To go from B to A, we simply slowly lower the piston, allowing enough time for heat
to flow out into the large object to maintain the same temperature.
In general, in a reversible process, changes must occur very slowly so that there is
time for the system to adjust to a state of thermal equilibrium. The process itself
therefore goes through a succession of equilibrium states.
A process for a thermodynamic system that starts from one state and ends with the
same state is called a cyclic process. A cyclic process may or may not be reversible,
because there is in general change in the environment.
The recognition and analysis of irreversible transformations led to postulates with far
reaching consequences.
Postulate of the second law of dynamics (Kelvin Statement)
A transformation whose only final result is to transform into work heat
extracted from a source which is at the same temperature throughout is
impossible.
A source of heat that maintains the same temperature is called a heat reservoir. A
device that can extract heat from a single heat reservoir and convert the heat
35
completely into work with no other change in the environment is called a perpetuum
mobile of the second kind. (The first kind is one that generates work without the
expenditure of energy or the absorption of heat, which is forbidden by the first law of
thermodynamics). It does not violate the first law of thermodynamics. But the second
law states that it does not exist. If it existed, it would be possible to draw on the
practically infinite supply of heat from the ocean at no cost of materials.
Heat Engines
Fruitful analysis of the consequence of the postulate follows when we introduce a
heat engine. This is a device employing a substance such as a fluid that can take an
amount of heat from a hot reservoir, reject another amount to a cold reservoir,
perform an amount of work on the environment, and return to the same state. The
substance that has returned to the same state is said to undergo a cyclic process called
a Carnot cycle. During one cycle of operation, if the amount of heat absorbed is Q1 ,
the amount rejected is Q2 , and the work performed is W , since there is no change in
internal energy of the substance, application of the first law of thermodynamics yields
U  Q1  Q2  W  0
so that Q1  Q2  W
A schematic diagram of a heat engine is as shown:
Q1
W
Q2
By definition, a reversible engine is one that can take Q2 back from the cold
reservoir, have the work W done on the working substance by the environment, and
delivers the heat Q1 back to the hot reservoir, while returning the substance to its
original state. Not all engines are reversible.
Consider two engines A and A’, with the corresponding heat and work in one cycle
denoted by Q, W and Q’, W’ respectively. We can show:
If A is reversible, then
36
Q1 Q1

Q2 Q2
If both A and A’ are reversible, then
Q1 Q1

Q2 Q2
To prove the first relation, we first scale the engines so that
Q2  Q2 .
We run the engine A’ one cycle, followed by a reversed cycle of A (This is possible
because A is reversible). If Q’1 > Q1, the amount of heat Q1  Q1 is extracted from the
hot reservoir while no heat is exchanged from the colder reservoir in one combined
cycle.
Q’1
Q1
W’
Q’1-Q1
W
=Q
Q2=Q2’
Q’2
=
Q
Further, from the first law, Q1  Q2  W 
Q1  Q2  W , it follows that
Q1  Q1  W   W
Thus, the amount of work done on the environment W’-W is positive. The net effect
of the combined cycle is therefore to extract heat from one reservoir and perform an
equal amount of work, while leaving no change anywhere. This is impossible
according to the postulate of the second law of thermodynamics. Hence we must have
Q1  Q1  0
37
W’-W
=Q
It then follows that
Q1 Q1
, proving the first assertion.

Q2 Q2
If A’ is also a reversible engine, by exchanging the roles of A and A’ in the forgoing
argument, we have
Q1 Q1

Q2 Q2
Taken together we prove the second assertion.
The efficiency  of a heat engine is defined as the fraction of heat absorbed that is
converted into work. It is given by

Q
W Q1  Q2

 1 2
Q1
Q1
Q1
Q2
is smaller for a reversible engine than an
Q1
irreversible one, we conclude that all reversible engines operating between the
same two heat reservoirs have the same efficiency, which is also larger than the
efficiency of irreversible engines.
Since we have shown that the ratio
Carnot Cycle with Ideal Gas
A reversible Carnot cycle can be realized using one mole of an ideal gas, operating
between heat reservoirs at temperatures T1 and T2, measured in K.
38
The cycle starts with the gas in state a, at temperature T1 and volume Va. It is allowed
to expand to the volume Vb in a reversible isothermal process to reach the state b. It is
then further expanded to a volume Vc in a reversible adiabatic process to reach state c
at the lower temperature T2. Then it is compressed isothermally to state d, with
volume Vd and at temperature T2. An adiabatic compression then brings the gas back
to state a.
The heat absorbed from the reservoir at T1 during the isothermal expansion is
V
Q1  RT1 ln b
Va
The heat rejected to the colder heat reservoir during the isothermal compression is
Q2  RT2 ln
Vc
Vd
No heat is exchanged with the environment during the adiabatic processes, although
both temperature and volume change would change. During the adiabatic expansion b
to c, it can be shown that
T1Vb 1  T2Vc 1
Similarly, during the adiabatic expansion d to a:
T1Va 1  T2Vd 1
Taken together, we find
Vb Vc

V a Vd
The expressions for Q1 ,Q2 from the isothermal processes therefore imply
Q1 Q2

T1 T2
This shows that the efficiency of a reversible engine operating between heat
reservoirs of temperatures T1 and T2 is given by
  1
Q2
T
 1 2
Q1
T1
39
A large efficiency requires a high value of T1 and a low value of T2. Normally, the
lowest temperature we easily achieve is room temperature. So the only way to raise
efficiency is to raise the temperature T1. For example, in a steam engine, the high
temperature is 100°C so that T1=273+100=373K Taking the air temperature to be
20ºC, or T2=273+20=293K, the ideal efficiency is
1
293
 21%
373
For an internal combustion engine, the heated gas can reach 800°C, or 1073K. The
ideal efficient is
1
293
 73%
1073
In practice, the efficiency is much less.
Entropy
For a substance undergoing one Carnot cycle in a heat engine, absorbing the amount
of heat Q1 from a reservoir of temperature T1, and rejecting the heat Q2 to a reservoir
at temperature T2, we have
T1 Q1

T2 Q2
which can be written as
Q1  Q2 

0
T1
T2
with the equality sign holding if the cycle is reversible. Notice that –Q2 can be
considered as the heat absorbed by the substance.
More generally, it can be shown that if a thermodynamic system undergoes a cyclic
process in which a series of heat absorptions Q1 , Q2 , Q3 , take place from heat
reservoirs of various temperatures T1 , T2 , T3 , . , then

Q Q1 Q2



T
T1
T2
0
any cyclic process
with the equality sign holding if the process is reversible.
40
If the system undergoes a reversible transformation from state A to state B, the
quantity
B

A
Q
T
is independent of the path (consisting of a series of intermediate equilibrium states)
Q
taken, and therefore depends only on the states A and B. To prove this, let 
T
I
Q
and 
be the values for two reversible paths connecting A and B. Starting from
T
II
state A, following path I and the reverse of path II, we arrive back at A. Since during
the reverse process of II, heat absorption is Q from the reservoir of temperature T
where Q and T are for the forward process II, we have according to the reasoning
above for a reversible cyclic process,

I
 Q   0
Q

T
T
II
which proves our assertion.
The result allows us to introduce a new state variable called the entropy. The change
of entropy between states A and B is defined as
B
S  S B  S A  
A
Q
T
reversible process from A to B
where the sum is over a reversible path.
For any process I from A to B, we can complete a cyclic process with a reversible
process II from B to A. Applying the definition of entropy to the path II:
A
S A  SB  
B
Q
T
reversible process from B to A
The inequality
B

A
Q A Q

 0 cyclic process from A back to A
T
T
B
for any cyclic process can be written
41
B

A
Q
 S A  SB  0
T
.
so that
B
SB  S A  
A
Q
T
for any process from Ato B
An isolated system is one that does not exchange heat with its environment. For such
a system, the right hand side of the above equation is zero. Thus, entropy does not
decrease in an isolated system, and in fact, tends to increase as real processes, not
being ideal, are irreversible.
Examples of entropy increase
1. Frictional Heating. In Joule’s experiment, water is heated by paddles driven by a
falling weight. Consider the water and the falling weight together forming an
isolated system. There is no change of entropy associated with the falling weight,
but the entropy of the water increases. This is because the rise in temperature of
the water can be achieved also by reversible heat flow in which the water is
brought into contact with heat reservoirs of successively higher temperatures.
2. Conduction of heat from a hot object to a cold object. An ice cube at 0°C in a
room at a higher temperature melts gradually while the temperature stays the
same. Consider the air in the room and the ice cube to form an isolated system.
The heat flow away from the air can be taken to be a reversible process, causing a
change of entropy

Q
Troom
of the air. The same quantity of heat Q is absorbed by the ice, although the
process is not reversible. However, the same change in the state of the ice,
namely, the melting of a certain amount of ice at the temperature 0°C, can be
effected by the slow (reversible) absorption of the same amount of heat. The
change in entropy of the ice is therefore
Q
Tice
The net change of entropy is

Q Q

Troom Tice
and is positive because Troom  Tice
42
3. Free expansion of a gas. Consider a thermally insulated rigid container to be
divided into two compartments, with an ideal gas on one side and vacuum on the
other. Upon removal of the partition, the gas expands to fill the whole volume.
According to the first law of thermodynamics, there is no change in internal
energy of the gas, because the gas does no work in expanding into a vacuum, and
there is no exchange of heat. Hence the temperature remains unchanged because
the internal energy of an ideal gas depends only on temperature but not volume.
The final state of the gas can also be arrived at starting from the initial state by a
reversible isothermal expansion. During this process, the gas absorbs the amount
of heat
Vf
Q  nRT ln
Vi
where Vi and V f are its initial and final volumes. (This result was obtained when
we considered applications of the first law to ideal gas processes.) Therefore, by
definition, the change of entropy of the gas is
Vf
Q
 nR ln
T
Vi
and is positive because V f  Vi .
The fact that the entropy of an isolated system always increases can be understood
to define an arrow of time: the flow of time is in the direction of entropy
increase.
43