Download Lecture 5 Molecular Orbital Theory Part 1 Molecular Orbital Theory

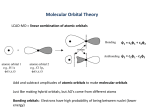
Lecture 5 Molecular Orbital Theory
_____________________________________________________________________________
Part 1
Part 2
Part 3
Molecular Orbital Theory
Applications of MO Theory
Theories of Chemical Bonding
________________________________________________________________________________
Part 1
Molecular Orbital Theory
Electrons in atoms are held in atomic orbitals (AOs). When a covalent bond
is formed between atoms, the shared electrons occupy a new orbital formed
by merging the two AOs. This is called a molecular orbital MO.
As is the case for AOs, the two electrons in the MO are spin paired,
i.e. they have spins +½ and -½.
Consider the hydrogen molecule, H2.
Imagine the two hydrogen atoms initially separated by a large distance,
being brought closer together; the s-orbitals on each atom begin to overlap,
until the two nuclei are so close together that electronic and nuclear
repulsion prevents further approach.
We say that the two atomic orbitals, AO’s, combine together to form
two molecular orbitals, MO’s.
H2 atomic orbitals
H2 molecular orbitals
node
σ*1s
+
1s
Energy
1s
σ1s
If the two waves are ‘out of phase’
i.e. a ‘+’ with a ‘-’, or a ‘-’ with a ‘+’
If the two waves are ‘in phase’
Note:
The meaning of the two symbols, σ1s and σ*1s, which label the two MOs will
be explained later.
Two MOs arise because the AOs are waves, so they can overlap in two
ways:
Either;
in phase - “constructive interference”
constituent AOs
Ψ
resulting MO
position of the two
hydrogen nuclei
Or;
out-of phase - “destructive interference”
Ψ∗
At this point Ψ = 0 ⇒ Ψ2 = 0
-this is called a node;
there is no probablity of
finding the electrons here
• The bonding MO is labeled Ψ, and the antibonding MO is labeled Ψ∗.
• So when two atomic orbitals combine they form two molecular orbitals
one will be a bonding MO (AOs in phase) & the other will be an
antibonding MO (AOs out-of-phase).
• If each AO contributed one electron, these now fill the bonding MO, this
is lower in energy than the constituent AOs. This results in stabilisation
of the system, this is the driving force for formation of the bond.
The interpretation of a molecular orbital is similar to that for atomic orbitals:
The square of the orbital evaluated at a given point in space is the
probability of finding an electron at that point.
Ψ
Ψ∗
Ψ2
(Ψ∗)2
Node;
Ψ* = 0, so (Ψ*)2 = 0
i.e. zero probability of finding
the electron between the nuclei
In the case of hydrogen, each atom has one electron, so when the two atomic
orbitals interact to from two molecular orbitals the bonding molecular orbital
has a lower energy than either atomic orbital - so both electrons can ‘fit’ into
bonding MO and the antibonding MO is empty.
Bonding MO:
• When the constituent AOs are in phase the result is a bonding orbital
• This MO can accommodate two electrons (usually one from each atom).
• The energy of the MO is lower than the energy of the two constituent
AOs, so placing two electrons in such an orbital results in a net
stabilisation of the system; the formation of a stable covalent bond.
• The MO energy is lower than the AO energy because the MO is larger;
so the space occupied by the electron is greater.
• The MO energy is also lower because it results in a region of high
electron density between the two nuclei. This screens the nuclei from
each other, reducing nuclear-nuclear repulsion. So the bonding MO has
lower energy than either AO because there is a large amount of electron
density on the vector joining the two nuclei.
Anti-bonding MO:
• When the constituent AOs are out-of-phase phase the result is an antibonding orbital. This is signified by an asterisk.
• In this case there is a region of space between two nuclei of zero electron
density (probability of finding an electron there), this is called a node.
• This results in the antibonding MO having higher energy than either AO.
• Like all orbitals, the antibonding MO can accommodate two electrons
(one from each atom). The energy of this MO is higher than the energy of
the constituent AOs; so putting electrons in this orbital results in
destabilisation of the system; usually however there are no electrons left
over to put into this orbital.
The relative stabilisation of the bonding MO and relative destabilisation
of the corresponding antibonding MO, as compared to the isolated
atoms, are large when:
1. The overlap between the atomic orbitals is large.
2. The atomic orbitals are close in energy.
strongly destabilised
weakly destabilised
σ*2pz
Energy
π*2px
+
2pz
+
2px
2pz
2px
π2px
σ2pz
weakly stabilised
strongly stabilised
Note (a) by convention the bond axis (line joining the atoms) is the z-axis
(b) the labels, π2pz etc., will be explained later
The 2pz-2pz overlap, shown on the left hand side is greater than the
equivalent 2px-2px overlap, as the 2pz orbitals on each atom point towards
the other atom; resulting in greater stabilisation.
This is more usually drawn as follows:
σ*2pz
AOs at the
same
energy
2pz
2pz
π*2px
2px
σ2pz
2px
π2px
This difference arises purely due to overlap considerations, as the 2pz and
2px orbitals are degenerate (of the same energy).
On the other hand, there is less interaction and hence less stabilisation or
destabilisation when:
• The overlap between the atomic orbitals is small.
• The atomic orbitals are widely separated in energy.
strongly destabilised
weakly destabilised
σ*2pz
Energy
σ*
+
2pz
+
2pz
σ2pz
2pz
σ
2s
weakly stabilised
strongly stabilised
σ*2pz
AOs at the
same energy
2pz
2pz
σ2pz
σ*
2pz
σ
2s
The reduced stabilisation/destabilisation, shown the right hand side, arises
due to the energy differences of the AOs. Even though there is reasonable
overlap between the 2pz and 2s orbitals in this case, the fact that these AOs
are not degenerate (in molecules) means there is not much stabilisation.
Mathematical version of MO theory:
This is entirely analagous to the pictorial view described above.
To chemists the pictorial view is more immediately useful, but we need to
look a bit at what an MO really is:
When two atomic orbitals (ϕa and ϕa on adjacent atoms A and B) interact the
resulting molecular orbitals (labelled ψ) are the linear combination of the
two atomic orbitals. This is known as the LCAO-MO approximation; it is
the central assumption if MO theory.
So the MO wavefunction is a linear combination of the AOs:
ψ = c1 ϕ a + c2 ϕ b
- where c1 and c2 are unknown constants (called the mixing coefficients) that
we must determine, and ϕa and ϕb are the AOs on atom a and atom b.
As in the case of AOs the meaning of ψ is undefined, however ψ2 is the
probability density of finding the electrons in a given place.
So:
ψ2
=
(c1 ϕa + c2 ϕ b)2
=
c12 ϕa2 + c22 ϕ b2 + 2c1c2 ϕa ϕ b
In this case, the H2 molecule, the two atoms are identical, so the probability
of finding electrons on either atom is the same.
i.e. c12 = c22.
This results in two solutions:
c1 = +1
c2 = + 1
This tells us that each atomic orbital contributes the same amount to the MO.
Note
The solution where c1 = -1, c2 = +1 is the same as c1 = +1, c2 = -1
-the sign of the coefficient determines the phase of the AO in the MO and all
that matters is whether the two AOs are in-phase (c’s both positive or both
negative) or out-of-phase (one c’s positive & the other negative).
So when two atomic orbitals combine they form two MO’s
ψ = ϕa + ϕ b
ψ* = ϕa - ϕ b
and
One can immediately see how MO theory can accommodate the two
situations where VB theory struggles:
(i)
Polar molecules:
VB theory assumes all electrons in covalent bonds are equally shared.
From simple electronegativity arguments we know that this is not the case.
In the MO description of polar covalent bonds, the coefficients on the more
electronegative atoms are larger, i.e. the probability of finding the electron in
the region of that atom is larger.
Example:
In the notional molecule, ClF. The bond is due to overlap between the 2pz
orbital on F, the more electronegative atom, and the 3pz on Cl.
Cl
3pz
ΨΜΟ = c1φ1 + c2φ2
F
2pz
where c2 > c1
φ1 is the 3pz on Cl
φ2 is the 2pz on F
(ii)
Resonance:
So far we have only looked at MO theory for diatomics. There is no reason
that AOs on several adjacent bonded atoms cannot overlap together, the only
restriction is that each MO can only accommodate two electrons.
Example:
The highest energy occupied MO (called the HOMO) of the planar molecule
benzene (C6H6) consists of the six 2pz orbitals (which point out of the
molecular plane) on each carbon atom overlapping, all in-phase. Thus the
two electrons in this MO are completely delocalised; they are equally likely
to be found in the vicinity of any of the six carbon atoms.
What types of overlap are possible?
(i)
σ-bonds;
atomic orbitals
molecular orbitals
node
σ*2pz
Energy
+
2pz
2pz
σ2pz
So a 1s-1s, or a 2s-2s interaction is also a σ (sigma) interaction.
i.e. H2, is held together with a σ-bond.
The label σ, is a symmetry label. If we rotate σ or σ∗ MOs through 360º
about the inter- nuclear axis. The resulting orbital does not change sign
during the rotation.
π-bonds;
(ii)
atomic orbitals
molecular orbitals
node
π*2px
Energy
+
2px
2px
π2px
Or:
+
2py
2py
Note:
• In this case, unlike for σ-bonds, there is no electron density on the vector
joining the two nuclei.
• The label π, is again a symmetry label. If we rotate π or π∗ MOs through
360º about the inter- nuclear axis. The resulting orbital changes sign
twice during the rotation.
It is not possible to rotate π-bonds:
+
H
+
H
-
H
H
The π-bond in ethene, C2H2.
Note rotating around this bond will remove
the overlap i.e. “break the π-bond”.
So rotation requires a lot of energy, as a result
ethene is rigidly planar.
This is not the case for σ-bonds.
Rotation does not break the bond.
So the ethylene molecule is planar and rigid.
H
H
C
H
C
H
VB theory agrees; it describes the bonding as being between two sp2
hysridised orbitals (which are planar) on each carbon.
So to summarise:
a σ-interaction
-
-
+ +
a σ∗-interaction
-
+ -
+
+
+
-
-
+
-
-
+
a π-interaction
a π∗-interaction
Note:
+
-
-
+
these two interactions
are exactly the same
all that matters is the
relative phase of the AOs
-
+
+
-
Some orbitals cannot overlap because of their orientation in space
atomic orbitals
+
+
_
no net interaction
⇒ no stabilisation
⇒ no molecular orbitals
_
+
2px
2pz, y
Other more complex overlaps are possible:
Two dx2-y2 orbitals can overlap when two metal atoms approach along the z
axis:
• This gives rise to δ bonding and δ* antibonding orbitals.
+
+
-
-
+
+
-
δ - interaction
-
+
+
-
+
-
-
+
δ∗ - interaction
• The label δ, is again a symmetry label. If we rotate δ or δ∗ MOs through
360º about the inter- nuclear axis. The resulting orbital changes sign four
times during the rotation.
MO diagrams of 2nd Row Diatomic Molecules
Now lets look at the overlap of several different AOs at once, as clearly
occurs when elements like C, N etc bond covalently:
Note that only the valence shell needs to be considered: The overlap of the
inner orbitals is negligibly small, as they are smaller. Thus for C, N, O etc
the 1s-1s overlap can be omitted.
The overlaps are as follows:
AOs atom1
MOs
AOs atom 2
σ∗2pz
*
π*2px, π2p
y
2p
π2px, π2py
2p
σ2pz
σ∗2s
2s
σ2s
2s
Expected MO diagram for 2nd row diatomic molecules
σ∗2pz
*
π*2px, π2p
y
π2px, π2py
2pz overlap is greater than 2px,2py
so stabilisation in bonding orbital and
destabilisation of antibonding MO greater
σ2pz
2px and 2py form
a degenerate pair
σ∗2s
σ2s
2s AOs are of lower energy
than 2p AO,
so the MOs are the same
• In this argument the overlap between the 2s orbital on one atom and the
2p on the other has been omitted.
• This overlap is weaker than the 2s-2s and 2p-2p, so we don’t have to
consider it explicitly.
• However it does have the effect of stabilising the σ2s MO and more
importantly destabilising the σ2p MO.
• This effect is large enough for B2, C2 and N2 to alter the energy ordering,
while for O2, F2 and Ne2 the effect is weaker and order of the orbitals is
as expected omitting this effect.
strong 2s-2p interaction
σ∗2pz
weak 2s-2p interaction
σ∗2pz
*
π*2px, π2p
y
*
π*2px, π2p
y
σ2pz
π2px, π2py
π2px, π2py
σ2pz
σ∗2s
σ∗2s
σ2s
σ2s
observed for
observed for
B2, C2, N2
O2, F2, Ne2
The main points of Molecular Orbital theory:
• MO theory assigns electrons in a molecule to a series of orbitals
• Like atomic orbitals, MOs are wavefunctions. We can relate them to the
probability of finding electrons in certain regions of a molecule.
• The number of MOs formed is equal to the number of AOs combined.
• Of the two MOs formed when two AOs are combined, one is a bonding
molecular orbital at lower energy than the original atomic orbital. The
other is an antibonding MO of higher energy.
• Electrons normally enter the lowest energy MO available to them
• The maximum number of electrons in a given MO is two (Pauli
Exclusion Principle).
• Electrons enter orbitals of identical energy singly before they pair up
(Hunds rule). If a molecular species is to be stable it must have more
electrons in bonding than in antibonding MOs.
• For AOs of very different energies the stabilisation of the lowest energy
MO w.r.t. the lowest energy AO is very small.
• Conversely the destabilisation of the highest energy MO w.r.t the highest
energy atomic orbital is very small.
Part 2
Applications of MO Theory
Bond Order
The bond order is a convenient measure of the strength of a covalent bond;
it is defined as:
BO = ½[no. of bonding electrons – no. of antibonding electrons]
Consider molecular oxygen, O2, the MO diagram is:
σ∗2pz
*
π*2px, π2p
y
π2px, π2py
σ2pz
σ∗2s
σ2s
So its BO = ½(8 – 4) = 2
This makes sense as O2 has a double bond.
Its Lewis structure is:
O
O
Now consider molecular nitrogen, N2, the MO diagram is:
σ∗2pz
*
π*2px, π2p
y
σ2pz
π2px, π2py
σ∗2s
σ2s
So its BO = ½(8 – 2) = 3
This makes sense as N2 has a triple bond.
Its Lewis structure is:
N
N
Magnetic Properties of Atoms and Molecules
A spinning charge induces around it a magnetic field. This is true for an
electron. The direction of the magnetic field depends on the direction of the
electronic spin, i.e. ms = +½, or ms = -½.
Diamagnetism
In a diamagnetic substance all spins are paired, i.e. there are equal numbers
of electrons of each spin. The net magnetic moment of the material is zero,
so it is unaffected by any external magnetic field that might be applied.
Paramagnetism
In a paramagnetic substance unpaired electrons are present. The net
magnetic moment of the material is non-zero, so it may be affected by an
external magnetic field. For instance such molecules may be attracted to the
poles of a bar magnet.
• On this basis molecular nitrogen, N2, is diamagnetic.
• While molecular oxygen, O2, is paramagnetic. This expectation is
confirmed by experiment.
Exercise:
Construct MO diagrams for B2, C2, N2, O2, F2, Ne2, (O2)2- and (O2)2+ and
determine the bond order and whether the molecules are diamagnetic or
paramagnetic.
Excited States of Molecules
Electronic transitions in molecules occur between molecular orbitals, so we
must consider:
i)
the form of the orbitals, and
ii)
which transitions are allowed.
Molecular Orbital Diagram for H2:
AOs, hydrogen 1
MOs
σ∗2pz
π∗2px, π∗2py
AOs, hydrogen 2
σ∗2s
2s, 2p
σ2s
π2px, π2py
σ2pz
2s, 2p
σ∗1s
1s
1s
σ1s
The ground state is σ1s2.
The * denotes an anti-bonding orbital.
Only two transitions are observed:
H2
H2
(σ 1s 2 ) +
(σ 1s 2 )
hν (110.9 nm)
+ hν (100.2 nm)
→
H2
(σ 1s1 , σ 2 p1 )*
z
→
H2
(σ 1s1 ,π 2 p1 )*
x
or H2
(σ 1s1 , π 2 p1 )*
y
where px & py are degenerate (same energy)
This can be shown diagramatically:
________________
(σ 1s1 ,π 2 p1 )*
x,y
________________
(σ 1s1 , σ 2 p1 )*
z
110.9 nm
100.2 nm
E↑
________________
(σ 1s 2 )
Note:
• Remember (as in the case of the hydrogen atom) the transitions are
stimulated by light (electromagnetic radiation). Only light of a frequency,
ν, corresponding to the energy difference, ∆E, between the orbitals can
cause a transition:
∆E = hν
-where h is Planck’s constant
• As the electron goes into an antibonding orbital, the bond order of either
of the excited states is zero.
• So promoting the electron into an antibonding orbital weakens the bond.
• This can result in the bond breaking. There is an entire branch of
chemistry, called photochemistry, which involves studying these excited
states and using light to synthesise new molecules.
• Applying heat can also break bonds (& this is the usual method) but can
you guess why using light might allow one to selectively break a
particular bond?
Part 3
Theories of Chemical Bonding
If MO theory is superior; why not use it all of the time instead of VB?
The simple answer is that we use whichever theory is more convenient for
describing the bonding in the molecule we are dealing with:
VB theory is good for describing the bonding in extended σ-bonded
carbon networks.
H3 C
C
H2
H2
C
C
H2
H2
C
C
H2
H2
C
C
H2
H2
C
C
H2
H2
C
C
H2
CH3
eg C13H28
• This is largely because the chains are often free to rotate about the C-C
bonds. Thus the overlaps between AOs, which MO theory relies upon to
explain the bonding, are continually being broken.
• In the VB description of such a molecule, two of the sp3 hybrids point
along the carbon chain and the other two overlap with a hydrogen 1s
orbitals, so every carbon on the chain is sp3 hybridised (tetrahedral).
• Thus the local geometry is well defined, but the actual shape is complex
and mobile. Can you guess why?
Hint does rotating about any of the carbon-carbon bonds break any orbital
overlaps?
However valence bond theory fails when:
1. There are odd numbers of electrons present
2. The structure is poorly represented by a single Lewis structure –
resonance.
3. Sometimes hybridised AOs are a better approximation of the orbitals
which overlap to form the bonds.
4. Most importantly, VB theory assumes that all bonded pairs of electrons
are the same; that they are equally shared between pairs of atoms. Thus it
assumes that all bonds are 100% covalent. This is really only the case for
homonuclear diatomic molecules, i.e. H2, Cl2 etc..
Example H2O vs H2S:
• In H2O the AOs on oxygen can be considered to undergo sp3
hybridisation; these hybrid orbitals overlap with the incoming 1s AOs on
the two hydrogens.
..
..
H
Isolated O atom
Hybridised O atom
→
2s22p4
H
O
6 “sp3”
This results in an OHO angle slightly less than the ideal tetrahedral value of
109.5°, as the lone pairs occupy the other two hybrids and have a greater
spatial requirement. Experiment confirms this expectation.
• One would expect that a similar picture emerges, the 3s and 3p orbitals
on sulphur should hybridise, resulting in a similar geometry to H2O.
• Experimentally the OHO angle is 92°.
• This is very close to the value of 90°, one would expect if the overlap is
between the unhybridised 3p-orbitals on sulphur and the AO of
hydrogen.
• The explanation is as follows:
(i)
The 3p orbitals are further from the nucleus so their mutual
repulsion is less than for 2p
(ii)
The orbitals are larger for S, so the bonds are longer. This
reduces repulsions between atoms bonded to the central atom.
Molecular orbital theory is more applicable for:
1. Molecules with odd numbers of electrons present
2. Molecules with highly polar bonds
3. Molecules exhibiting resonance
4. Transition metal complexes
It is beyond the scope of this course, but you should be aware that MO
theory also fails to reproduce the bonding and geometry of certain classes of
molecules.
Summary
Lecture 5
Molecular Orbital Theory
• Molecular orbital theory is a more general approach to understanding
covalent bonding.
• MO theory relies on the LCAO-MO approximation, which states that the
orbitals in which electrons in molecules are found, can be determined by
taking linear combinations of the AOs of the constituent atoms.
• MO theory successfully describes the bonding and properties of a wide
range of molecules, including single-electron species, polar covalent
molecules and molecules exhibiting resonance.