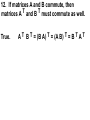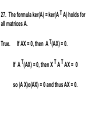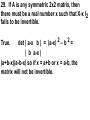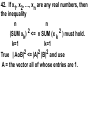Download (A T ) -1

Math 307
Spring, 2003
Hentzel
Time: 1:10-2:00 MWF
Room: 1324 Howe Hall
Instructor: Irvin Roy Hentzel
Office 432 Carver
Phone 515-294-8141
E-mail: [email protected]
http://www.math.iastate.edu/hentzel/class.307.ICN
Text: Linear Algebra With Applications,
Second Edition Otto Bretscher
Previous Assignment
Friday, Mar 28 Chapter 5.5
Page 240 Problems 1 through 43
1. If matrix A is orthogonal, then matrix A2
must be orthogonal as well.
True. Orthogonal matrices are closed under
multiplication.
T
T
T
2. The equation (AB) = A B holds for all
nxn matrices A,B.
False. The correct version is (AB) T = B T A T.
||01||00|| T= |10| T = |10|
||00||10||
|00|
|00|
|01|T |00|T
|00| |10|
= |00||01|=|00|
|10||00| |01|
3. If A and B are symmetric nxn matrices,
then A+B must be symmetric as well.
True. Symmetric matrices are a subspace.
4. If matrices A and S are orthogonal, then
S -1 A S is orthogonal as well.
True. The product of orthogonal matrices is
orthogonal.
5. All nonzero symmetric matrices are
invertible.
False.
A counter example is | 1 1 |
| 11 |
which has rank 1.
T
6. If A is an nxn matrix such that A A = I, then
A must be an orthogonal matrix.
True.
Since A is square, A T = A -1 and so
A T A = I. Thus, the columns of A are
orthonormal.
n
7. If V is a unit vector in R , and L = span[V],
then
Proj
False.
L(X) = (X o V)X for all vectors x in R n.
This does not project into < V >.
L(X) = (XoV) V
8. If A is a symmetric matrix, then 7 A must be
symmetric as well.
True. The symmetric matrices are a
subspace.
n
9. If T is a linear transformation from R
to
R n such that
T(E1),T(E2), ..., T(En) are all unit vectors,
then T must be an orthogonal transformation.
False.
| 1 1 | is a counter example.
|00|
10. If A is an invertible matrix, then the
equation
(A T) -1 = (A -1) T must hold.
True.
I = (A A -1) T = (A -1) T A T
11. If A and B are symmetric n x n matrices,
then A B B A must be symmetric as well.
True (A B B A) T = A T B T B T A T = A B B A
12. If matrices A and B commute, then
T
T
matrices A and B must commute as well.
True.
A T B T = (B A) T = (A B) T = B T A T
5
13. There is a subspace V of R such that
dim(V) = dim(V _|_), where V _|_ denotes the
orthogonal complement of V.
False: Dim (V) + Dim(V_|_) = 5
so they cannot be equal.
14. Every invertible matrix A can be
expressed as the product of an orthogonal
matrix and an upper triangular matrix.
True. This is the A = Q R decomposition.
n
15. If X and Y are two vectors in R , then the
equation
|X+Y| 2 = |X| 2 + |Y| 2 must hold.
False. This only holds when the vectors are
orthogonal.
16. If A is an n x n matrix such that | A U | = 1
for all unit vectors U, then A must be an
orthogonal matrix.
True. This means that | A X | = | X | for all X
and so A is an orthogonal matrix,
T
17. If matrix A is orthogonal, then A must be
orthogonal as well.
True. If A is orthogonal, then A must be
square and A T A = I means that A A T = I so
A T is orthogonal as well.
18. If A and B are symmetric n x n matrices,
then AB must be symmetric as well.
FALSE.
|01| |10| = |00|
|10| |00|
|10|
is a counter example
n
19. If V is a subspace of R and X is a vector
in R n, then the inequality
X o Proj V X >= 0 must hold.
True.
Suppose Y+N = X where Y is in V
and N is perpendicular to V.
Y = Proj V X and Y o Y >= 0 and Y o N = 0
YoY+YoN=YoX
So YoX = YoY >= 0.
20. If A is any matrix with ker(A) = {0}, then
T
the matrix A A represents the orthogonal
projection onto the image of A.
False. This is true if the columns of A are
orthonormal. If not, one
has to use
A (A T A) -1 A T
21. The entries of an orthogonal matrix are all
less than or equal to 1.
True. Since there squares all add to 1, each
has to be at most 1.
22. For every nonzero subspace of R n there
is an orthonormal basis.
True. This is the Gram-Schmidt Process.
23.
| 3 -4 | is an orthogonal matrix.
|4 3|
False. The columns are not of unit length.
n
24. If V is a subspace of R and X is a vector
n
in R , then vector proj V X must be
orthogonal to vector X- Proj V X
True. The projection is perpendicular to the
space and proj V X is in the space, so
proj V X is perpendicular to X-proj V X
25. If A and B are orthogonal 2x2 matrices,
then A B = B A.
False.
| 1 -1 | | 1 1 | = | 0 1 |
| 1 1 | | 1 -1 |
|1 0|
----------- --------Sqrt[2] Sqrt[2]
| 1 1 | | 1 -1 | = | 1 0 |
| 1 -1 | | 1 1 |
| 0 -1 |
----------- --------Sqrt[2] Sqrt[2]
26. If A is a symmetric matrix, vector V is in
the image of A and W is in the kernel of A,
then the equation VoW = 0 must hold.
True.
VoW = V T W = (AX) T W
=XTATW=XTAW=0
T
27. The formula ker(A) = ker(A A) holds for
all matrices A.
True.
If AX = 0, then A T(AX) = 0.
If A T(AX) = 0, then X T A T AX = 0
so (A X)o(AX) = 0 and thus AX = 0.
T
T
28. If A A = A A for an n x n matrix A, then
A must be orthogonal.
False. It is true for any symmetric matrix
including | 1 1 |.
|11|
29. If A is any symmetric 2x2 matrix, then
there must be a real number x such that X-x I2
fails to be invertible.
det | a-x b | = (a-x) 2 – b 2 =
| b a-x |
(a+b-x)(a-b-x) so if x = a+b or x = a-b, the
matrix will not be invertible.
True.
T
30. If A is any matrix, then matrix 1/2(A-A )
is skew-symmetric.
False: If A is not Square, then A-AT is not
defined. If A is Square, then it is true.
( 1/2(A-A T)) T = 1/2 (A T – A )
= -1/2 (A - A T).
31. If A is an invertible matrix such that
-1
A = A, then A must be orthogonal.
False.
A = | 1 b | Squares to the identity.
| 0 -1 |
32. If the entries of two vectors V and W in
R n are all positive, then V and W must
enclose an acute angle.
True. Since V o W is positive, Cos[theta] is
positive and theta < Pi/2.
33. The formula (ker B) _|_
for all matrices A.
= im( B T ) holds
True. It simply says that B ker(B) = 0.
T
34. The matrix A A is symmetric for all
matrices A.
True.
(A T A) T = A T A.
35. If matrix A is similar to B and A is orthogonal,
them B must be orthogonal as well.
False.
| 1 -1 | | 1 -1 | | 1 1 |
|0 1||1 1||0 1|
-------Sqrt[2]
1/Sqrt[2] | 0 -2 | | 1 1 |
|1 1||0 1|
1/Sqrt[2] | 0 -2 |
|1 2 |
T
36. The formula Im(B) = Im(B B) holds for
all square matrices B.
False.
| 01|
|00 |
has image | x |
|0|
B T B = | 0 0 | | 0 1 | = | 0 0 | has image | 0 |
|1 0 | | 0 0 | | 0 1 |
|x|
37. If matrix A is symmetric and matrix S is
-1
orthogonal, then matrix S A S must be
symmetric.
True.
S T A S is symmetric when A is.
39. There are orthogonal 2x2 matrices A and B
such that A+B is orthogonal
` as well.
True.
| ½
-Sqrt[3]/2 | | ½
+Sqrt[3]/2 |
| +Sqrt[3]/2 ½
| | -Sqrt[3]/2 ½ |
Are two orthogonal matrices which add to I2.
n
40. If | AX | <= | X | for all X in R , then A must
represent the orthogonal projection onto a
subspace V of R n.
False: Let A = ½ I.
41. Any Square matrix can be written as the
sum of a symmetric and a skew-symmetric
matrix.
True A = ½ (A +A T) + ½ (A – A T).
42. If x1, x2, …, xn are any real numbers, then
the inequality
n
n
(SUM xk) 2 <= n SUM (x k 2 ) must hold.
k=1
k=1
True | AoB|2 <= |A|2 |B|2 and use
A = the vector all of whose entries are 1.
T
2
43. If A A = A for a 2x2 matrix A, then A
must be symmetric.
True.
A(AT – A) = 0
If A is not symmetric, then the first and
second columns of A have to be zero.