* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Stat 100, This week
Survey
Document related concepts
Transcript
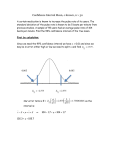
Stat 100 March 20 • Chapter 19, Problems 1-7 • Reread Chapter 4 Basic statistical problem • Use a sample to estimate something about a population • Example: Use sample of n = 50 students to estimate mean number of classes missed per week by all PSU students Margin of Error • A sample is not likely to match the population exactly • Margin of error = likely upper bound on sampling error • Difference between sample result and population value is likely to be smaller than the margin of error. Confidence Interval • Confidence interval is an interval that is likely to catch a population value. • Confidence level = probability procedure provides interval that captures population value. • Most common confidence level is 95% Calculating a Confidence Interval • Sample estimate ± margin of error • Last time we looked at percents • Today, we look at estimating averages (means) Margin of Error for Sample Mean • SEM = “standard error of the mean” • SEM= SD of data / sqrt(n) • Margin of error for a mean = 2 × SEM =2 × [SD of data / sqrt(n)] Example of Estimating a Population Mean • Spring ‘98 Stat 100 survey included question about hours of sleep the previous night. • For n = 190 students, mean was 7.1 hours and standard deviation was 1.95 hours. Nightly Hours of Sleep n=190 Spring '98 students 25 Percent 20 Mean = 7.11 , SD = 1.95 15 10 5 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Hours of Sleep Basic elements of the problem • Population = all 40,000 PSU students • Sample = 190 students in Stat 100 • Value of interest = mean hours of sleep the previous night • Sample mean = 7.1 hours • Objective: Estimate mean hours of sleep for population Margin of error for the sample mean • Margin of error= 2 × SEM = 2 × [SD/sqrt(n)] • SD of data = 1.95, and n = 190 • Margin of Error = 2 × [1.95/sqrt(190)] = 0.28 hours (About 0.3 hours) • Interpretation: It is likely that the sample mean is within 0.3 hours of the population mean 95% Confidence Interval for Population Mean • Sample mean ± margin of error • 7.1 ± 0.3 hours, or from 6.8 to 7.4 hours. • 95% confident that in the population, mean hours of sleep is between 6.8 and 7.4. Using interval to test hypotheses • Somebody claims that average amount of sleep for students is 6 hours per night. • What does our interval indicate about this claim? • Interval estimate of population mean was 6.8 to 7.4 hours. • Seems safe to reject claim that mean is 6 because evidence (the interval) is that mean is higher. Another hypothesis • Claim is made that mean hours of sleep is 7 hours for college students. • Claim acceptable: It’s consistent with our estimate that the mean is between 6.8 and 7.4 hrs. How many classes do you skip per week? • For n = 554 women in Stat 200 Mean = 1.09 and SD = 1.32 • For n = 321 men in Stat 200 mean=1.65, SD=1.85 Some problems • Use the data to estimate mean classes skipped per week for all PSU women. • Use the data to estimate mean classes skipped per week for all PSU men • Determine if there’s a difference between men and women when it comes to skipping Confidence interval for women • Margin of error =2×[SD/sqrt(n)] = 2×[1.32/sqrt(554)] =0.12 • Interval is 1.09 ± 0.12 , or from 0.97 to 1.21 classes skipped per week. • This estimates mean for all 20,000 women at PSU Confidence interval for men • Margin of error =2×[SD/sqrt(n)] = 2×[1.85/sqrt(321)]= 0.20 • Interval is 1.65 ± 0.10, or from 1.45 to 1.85 classes skipped per week. • This estimates mean for all PSU men Is there a difference? • Estimated mean for women: Between 0.97 and 1.21 • Estimated mean for men: Between 1.45 and 1.85 • Range of estimates clearly higher for men. Safe to conclude men skip more classes.