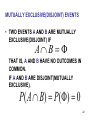Download PROBABILITY MODELS: FINITELY MANY OUTCOMES

CHAPTER 7
PROBABILITY,
PROBABILITY RULES, AND
CONDITIONAL
PROBABILITY
1
PROBABILITY MODELS: FINITELY
MANY OUTCOMES
DEFINITION:
PROBABILITY IS THE STUDY OF
RANDOM OR NONDETERMINISTIC
EXPERIMENTS. IT MEASURES THE
NATURE OF UNCERTAINTY.
2
PROBABILISTIC TERMINOLOGIES
• RANDOM EXPERIMENT
AN EXPERIMENT IN WHICH ALL
OUTCOMES (RESULTS) ARE KNOWN
BUT SPECIFIC OBSERVATIONS
CANNOT BE KNOWN IN ADVANCE.
EXAMPLE 1:
• TOSS A COIN
• ROLL A DIE
3
SAMPLE SPACE
•
THE SET OF ALL POSSIBLE OUTCOMES OF
A RANDOM EXPERIMENT IS CALLED THE
SAMPLE SPACE.
•
NOTATION:
•
EXAMPLE 2
S
1. FLIP A COIN THREE TIMES
S=
4
EXAMPLE 3
• AN EXPERIMENT CONSISTS OF FLIPPING A
COIN AND THEN FLIPPING IT A SECOND TIME
IF A HEAD OCCURS. OTHERWISE, ROLL A
DIE.
• RANDOM VARIABLE
THE OUTCOME OF AN EXPERIMENT IS
CALLED A RANDOM VARIABLE. IT CAN ALSO
BE DEFINED AS A QUANTITY THAT CAN TAKE
ON DIFFERENT VALUES.
5
EXAMPLE 4
• FLIP A COIN THREE TIMES. IF X
DENOTES THE OUTCOMES OF THE
THREE FLIPS, THEN X IS A RANDOM
VARIABLE AND THE SAMPLE SPACE IS
•S=
{HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
• IF Y DENOTES THE NUMBER OF HEADS
IN THREE FLIPS, THEN Y IS A RANDOM
VARIABLE. Y = {0, 1, 2, 3}
6
EVENTS
• AN EVENT IS A SUBSET OF A SAMPLE
SPACE, THAT IS, A COLLECTION OF
OUTCOMES FROM THE SAMPLE SPACE.
• EVENTS ARE DENOTED BY UPPER CASE
LETTERS, FOR EXAMPLE, A, B, C, D.
• LET E BE AN EVENT. THEN THE
PROBABILITY OF E, DENOTED P(E), IS
GIVEN BY
n
P ( E )   P ( wi )
i 1
7
Probability of an Event, E
• LET E BE ANY EVENT AND S THE
SAMPLE SPACE. THE PROBABILITY OF
E, DENOTED P(E) IS COMPUTED AS
n( E )
P( E ) 
n( S )
8
Probability of an Event
• The probability of an event A, denoted
by P(A), is obtained by adding the
probabilities of the individual outcomes
in the event.
•
When all the possible outcomes are
equally likely,
number of outcomes in event A
P( A) 
number of outcomes in the sample space
9
Probabilistic Terminologies
• The sample space of a random phenomenon
is the set of all possible outcomes. It is
usually denoted by S.
• An event is an outcome or a set of outcomes
(subset of the sample space).
• A probability model is a mathematical
description of long-run regularity consisting
of a sample space S and a way of assigning
probabilities to events.
10
Probability Rules
• Rule 1:
– A probability is a number between 0 and 1.
For any event A, 0 ≤ P(A) ≤ 1.
– A probability can be interpreted as the
proportion of times that a certain event
can be expected to occur.
– If the probability of an event is more than
1, then it will occur more than 100% of the
time (Impossible!).
11
Probability Rules
• Rule 2:
– All possible outcomes together must have
probability 1. P(S) = 1.
– Because some outcome must occur on
every trial, the sum of the probabilities for
all possible outcomes must be exactly
one.
– If the sum of all of the probabilities is less
than one or greater than one, then the
resulting probability model will be
12
incoherent.
Probability Rules
• We can use graphs to represent probabilities and
probability rules.
• Venn diagram:
S
A
Area = Probability
P(S) = 1; 0 ≤ P(A) ≤ 1
13
EXAMPLE 5
1. A COIN IS WEIGHTED SO THAT HEADS IS
TWICE AS LIKELY TO APPEAR AS TAILS.
FIND P(T) AND P(H).
2. THREE STUDENTS A, B AND C ARE IN A
SWIMMING RACE. A AND B HAVE THE
SAME PROBABILITY OF WINNING AND
EACH IS TWICE AS LIKELY TO WIN AS C.
FIND THE PROBABILITY THAT B OR C
WINS.
14
Probability Rules
• Rule 3 (Complement Rule):
– The probability that an event does not occur is 1
minus the probability that the event does occur.
– The set of outcomes that are not in the event A is
called the complement of A, and is denoted by AC.
– P(AC) = 1 – P(A).
– Example 6: what is the probability of getting at
least 1 head in the experiment of tossing a fair
coin 3 times?
HHH
HHT
HTH
HTT
THH
THT
TTH
TTT
15
COMPLEMENT OF AN EVENT
• THE COMPLEMENT OF AN EVENT A WITH
RESPECT TO S IS THE SUBSET OF ALL
ELEMENTS(OUTCOMES) THAT ARE NOT IN
A.
C
A
• NOTATION:
OR
'
A
P( A )  1  P( A)
C
16
Probability Rules
• Complement rule: P(AC) = 1 – P(A).
AC
A
17
Complement of an Event, A
18
Probability Rules
• Rule 4 (Multiplication Rule):
– Two events are said to be independent if
the occurrence of one event does not
influence the occurrence of the other.
– For two independent events A and B, the
probability that both A and B occur is the
product of the probabilities of the two
events.
– P(A and B) = P(A) X P(B).
19
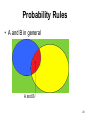
Probability Rules
• A and B in general
A and B
20
Probability Rules
• Rule 5 (Addition Rule):
– If two events have no outcomes in
common, they are said to be disjoint (or
mutually exclusive).
– The probability that one or the other of two
disjoint events occurs is the sum of their
individual probabilities.
P(A or B) = P(A) + P(B), provided that A
and B are disjoint.
21
MUTUALLY EXCLUSIVE(DISJOINT) EVENTS
• TWO EVENTS A AND B ARE MUTUALLY
EXCLUSIVE(DISJOINT) IF
A B  
THAT IS, A AND B HAVE NO OUTCOMES IN
COMMON.
IF A AND B ARE DISJOINT(MUTUALLY
EXCLUSIVE),
P ( A  B )  P ( )  0
22
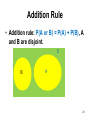
Addition Rule
• Addition rule: P(A or B) = P(A) + P(B), A
and B are disjoint.
S
B
A
23
Example 7
• Consider tossing a fair die.
– What is the sample space?
– Let A be the event that the outcome is odd
and let B be the event that the outcome is
a multiple of 3.
•
•
•
•
What is (A or B)?
What is (A and B)?
What is the complement of A?
Are A and B disjoint?
24
Example 8
• Consider selecting a card from an ordinary deck of
52 cards. Assume the cards are well-shuffled. Let
• A = {the selected is black}
• B = {the selected is a picture card}
• C = {the selected is an ace}
– What is A and B?
– What is B or C?
– What is A complement?
– Are B and C disjoint?
25
Example 9
• The American Red Cross says that
about 45% of the U.S. population has
Type O blood, 40% Type A, 11% Type
B, and the rest Type AB. Someone
volunteers to give blood. What is the
probability that this donor
– has Type AB blood?
– has Type A or Type AB?
– is not Type O?
26
Example 10
• The American Red Cross says that
about 45% of the U.S. population has
Type O blood, 40% Type A, 11% Type
B, and the rest Type AB. Among four
potential donors, what is the probability
that
– all are Type O?
– no one is Type AB?
– they are not all Type A?
– at least one person is Type B?
27
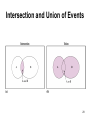
Intersection and Union of Events
• INTERSECTION OF EVENTS
THE INTERSECTION OF TWO EVENTS A AND
B, DENOTED
A B
IS THE EVENT
CONTAINING ALL ELEMENTS(OUTCOMES)
THAT ARE COMMON TO A AND B.
28
Intersection and Union of Events
29
UNION OF EVENTS
• THE UNION OF TWO EVENTS A AND B,
DENOTED,
A B
IS THE EVENT CONTAINING ALL THE
ELEMENTS THAT BELONG TO A OR B OR
BOTH.
30
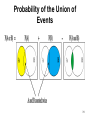
Probability of the Union of
Events
31
Probability Rule 6 – The General
Addition Rule
• For two events A and B, the probability
that A or B occurs equals the
probability that A occurs plus the
probability that B occurs minus the
probability that A and B both occur.
P(A or B) = P(A) + P(B) – P(A and B).
32
The General Addition Rule
• A ={students in Spanish class} and B = {students in French
class}
• “A or B =
•
A + B – (A and B)”
B
A
–
–
–
–
A or B in terms of color: Blue, Red, Yellow
A in terms of color: Red, Yellow
B in terms of color: Blue, Red
A and B in terms of color: Red
33
Example 11
• An elementary school is offering 2 language classes:
one in Spanish, and one in French. There are 60%
students in the Spanish class, 56% in the French
class, and 30% students in both language classes.
– What percent of students are in either Spanish
class or French class or both?
– If one student is randomly selected from this
school, what is the probability that she/he is in
either Spanish class or French class but not
both?
– For a randomly selected student, what is the
probability that she/he is only in Spanish class?
34
Example 12
• Suppose the probability that a U.S.
resident has traveled to Canada is 0.18,
to Mexico is 0.09, and to both countries
is 0.04. What is the probability that a
U.S. resident chosen at random has
– a) traveled to either Canada or Mexico or
both?
– b) traveled to Canada but not Mexico?
– c) not traveled to either country?
35
Example 12 Cont’d
• C ={traveled to Canada} and M = {traveled to Mexico}
M
C
–
–
–
–
–
Blue: to Mexico but not Canada
Red: to both Canada and Mexico--0.04
Yellow: to Canada but not Mexico
Blue and Red: to Mexico--0.09
Yellow and Red: to Canada--0.18
36
NULL EVENT: AN EVENT THAT HAS NO
CHANCE OF OCCURING. THE
PROBABILITY OF A NULL EVENT IS
ZERO.
P( NULL EVENT ) = 0
• CERTAIN OR SURE EVENT: AN
EVENT THAT IS SURE TO OCCUR.
THE PROBABILITY OF A SURE OR
CERTAIN EVENT IS ONE.
P(S) = 1
37
Conditional Probability
• The probability that the event B occurs
given that the event A occurs is called the
conditional probability of the event B given
the event A, and is denoted by P(B|A).
• Moreover,
P(A and B)
P(B | A) 
P(A)
38
Conditional Probability
39
Conditional Probability
A and B
40
Example 13
Nationwide Survey
Drink
Milk
Years
87-88
89-91 94-96 Total
Yes
354
502
366
1222
No
226
335
336
927
Total
580
837
732
2149
• If a young girl is randomly selected from all girls surveyed
during 87-88, 89-91, and 94-96, what is the probability that
– she reports drinking milk?
– she reports drinking milk and she is from the 89-91 survey ?
– she reports drinking milk if we know she is from the 89-91
survey?
41
Example 13 Cont’d
• For a randomly selected girl, the
probability that
– she reports drinking milk and she is
from the 89-91 survey is 502/2149;
– she is from the 89-91 survey is
837/2149;
– she reports drinking milk given that
she is from the 89-91 survey is
(502/2149)/(837/2149) = 502/837.
42
Example 14
• When choosing two cards from a deck
of well-shuffled cards, what is the
probability that the second card is
black?
43
GENERAL MULTIPLICATION RULE
• THE FORMULA FOR CONDITIONAL PROBABILITY
CAN BE MANIPULATED ALGEBRAICALLY SO THAT
THE JOINT PROBABILITY P(A and B) CAN BE
DETERMINED FROM THE CONDITIONAL
PROBABILITY OF AN EVENT. USING
P( A and B)
P( A B) 
P( B)
AND SOLVING FOR P(A and B), WE OBTAIN THE
GENERAL MULTIPLICATION RULE
P( A and B)  P( A B).P(B)
44
CONDITIONAL PROBABILITY
BAYE’S FORMULA THROUGH
TREE DIAGRAMS
45
BAYES’ FORMULA FOR TWO
EVENTS A AND B
• BY THE DEFINITION OF CONDITIONAL PROBABILITY,
P( A and B) P( A B).P( B)
P( B A) 

P( A)
P( A)

P( A B).P( B)
P( A B).P( B)  P( A B ).P( B )
C
C
46
Examples From Midterm II Practice
Sheet
47
Summary
•
•
•
Law of large numbers
Probability: Sample space / Events
Rules for probability model:
1. for any event A, 0 ≤ P(A) ≤ 1.
2. for sample space S, P(S) = 1.
3. if two events A and B are disjoint, then
P(A or B) = P(A) + P(B).
4. for any event A,
does not occur) = 1 - P(A).
5. For two independent events A and B,
P(A and B) = P(A) X P(B).
•
Venn diagram
P(A
48
Summary of Chapter
• General Addition Rule:
– For two events A and B,
P(A or B) = P(A) + P(B) – P(A and B).
• General Multiplication Rule
– For two events A and B,
P(A and B) = P(B|A) X P(A).
• Conditional probability
P(A and B)
P(B | A) 
P(A)
• Independence: P(B|A) = P(B).
49
Example 15 – Self Read
• 56% of all American workers have a workplace
retirement plan, 66% have health insurance, and 73%
have at least one of the benefits. We select a worker
at random.
– What is the probability that he has both health
insurance and a retirement plan?
– What is the probability that he has neither health
insurance nor a retirement plan?
– What is the probability that he only has a
retirement plan?
– Knowing that he has a retirement plan, what is the
probability that he has health insurance?
50
Example 15 – Self Read
• Solution:
– Let A be the event that he has a retirement plan.
– Let B be the event that he has health insurance.
– Then P(A)=0.56, P(B)=0.66, and P(A or B)=0.73.
A
B
51
Example 15 – Self Read
• Solution:
– What is the probability that he has both health insurance
and a retirement plan?
• P(A and B)=?
• General addition rule:
P(A or B) = P(A) + P(B) - P(A and B)
• Therefore, P(A and B) = P(A) + P(B) - P(A or B) =
0.56+0.66-0.73 = 0.49
A
B
52
Example 15 – Self Read
• Solution:
– What is the probability that he has neither health insurance
nor a retirement plan?
• The probability that he has at least one benefit is 0.73.
• Therefore, the probability that he has neither health
insurance nor a retirement plan is 1-0.73=0.27.
A
B
53
Example 15 – Self Read
• Solution:
– What is the probability that he only has a retirement plan?
• “Only has a retirement plan” means has a retirement
plan but no health insurance (not both).
• Therefore,
• P(he only has a retirement plan) = P(A) – P(A and B) =
0.56-0.49 = 0.07
A
B
54
Example 15 – Self Read
• Solution:
– Knowing that he has a retirement plan,
what is the probability that he has health
insurance?
P(B and A) 0.49
P(B | A) 

 0.875.
P(A)
0.56
55
Extra-Credit Exercise
• In a large Statistics lecture, the professor reports that 52% of
the students enrolled have never taken a Calculus course, 34%
have taken only one semester of Calculus, and the rest have
taken two or more semesters of Calculus. The professor
randomly assigns students to groups of three to work on a
project for the course.
– What is the probability that the first group member you meet
has studied some Calculus?
– What is the probability that the first group member you meet
has studied no more than one semester of Calculus?
– What is the probability that both of your two group members
have studied exactly one semester of Calculus?
– What is the probability that at least one of your group
members has had more than one semester of Calculus?
56
Extra-Credit Exercise
• A North American roulette wheel has 38 slots, of
which 18 are red, 18 are black, and 2 are green. If you
bet on red, the probability of winning is 18/38 =
.4737. The probability .4737 represents
(A) nothing important, since every spin of the
wheel results in one of three outcomes (red,
black, or green).
(B) the proportion of times this event will occur in
a very long series of individual bets on red.
(C) the fact that you're more likely to win betting
on red than you are to lose.
(D) the fact that if you make 100 wagers on red,
you'll have 47 or 48 wins.
57
Extra Credit Problems
1.
2.
A PAIR OF FAIR DICE IS TOSSED. FIND THE
PROBABILITY THAT THE MAXIMUM OF THE TWO
NUMBERS IS GREATER THAN 4.
ONE CARD IS SELECTED AT RANDOM FROM 50
CARDS NUMBERED 1 TO 50. FIND THE
PROBABILITY THAT THE NUMBER ON THE CARD
IS (I) DIVISIBLE BY 5, (II) PRIME, (III) ENDS IN THE
DIGIT 2.
58