Download Unit 1-6 Linear Equations

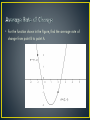
Today’s Topics:
• Writing Equations of Lines
• Parallel/Perpendicular
• Average Rate of Change
General Form of the Equation of a Line
The general form of the equation of a line is ax + by = c, where a,
b, and c are real numbers, with a and b not both equal to 0.
Forms of Linear Equations
General form
ax + by = c
where a, b, and c
are real numbers,
with a and b not
both equal to 0.
Point-slope
y – y1 = m(x – x1)
where m is the form
slope of the line
and (x1, y1) is a
point on the line.
Forms of Linear Equations
Slope-intercept
form
y = mx + b
where m is the
slope of the line and b
is the y-intercept.
Vertical line
x=a
where a is a constant,
and a is the x-coordinate
of any point on the line.
The slope is undefined.
Horizontal line
y=b
where b is a constant,
and b is the y-coordinate
of any point on the line.
The slope is 0.
A. Write the equation for the line that passes through the point (3
1, -5) and has slope in slope-intercept form.
4
A. Write the equation for the line that passes through the points
(-1, 3) and (2, 6) in point-slop form. Then write the line in
general form.
D.
Write the equation for the line that pass through the point (-1, 5)
and has a slope of zero in slope-intercept form.
C.
Write the equation of the line with slope of 4 and y-intercept of 2 in point-slope form.
Internet Advertising
The amount spent on Internet advertising was
$22.7 billion in 2009 and is expected to grow
at a rate of $2.25 billion per year for the next five years.
A. Write an equation for the amount of Internet advertising
spending as a function of the number of years after 2009.
B. Use the function to estimate the amount that will be spent on
internet advertising in 2015.
• Parallel Lines have the __SAME__ slope.
• Perpendicular Lines have slopes that are __NEGATIVE_
_RECIPROCAL__ of each other.
A. Write the equation of the line through (4, 5) and parallel to the
line with the equation 7x - 2y = -1.
B. Write the equation of the line through (2, -3) and
perpendicular to the line with the equation 2x + 3y -6 = 0.
Average Rate of Change
The average rate of change of f(x) with respect to x over the
interval from x = a to x = b (where a < b) is calculated as
changes in f (x ) values
average rate of change =
corresponding change in x -values

•
f  b   f a 
ba
• For the function shown in the figure, find the average rate of
change from point B to point A.
Difference Quotient
The average rate of change of the function f(x) from x to x + h is
f  x  h  f  x 
xhx
•

f  x  h  f  x 
h
For the function f(x) = x2 + 1, whose graph is shown,
f(x + h).
Difference Quotient
f x+h −f x
h
find
For the function 𝑓 𝑥 =
2𝑥 2
+ 1, find
𝑓 𝑥+ℎ −𝑓 𝑥
ℎ
.