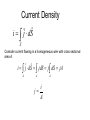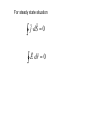Download Resistance does not vary with the applied voltage

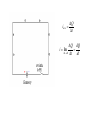
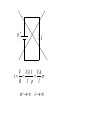
Current, Ohm’s Law, Etc.
dQ
i
dt
V
Ohm' s Law : R = ; R = Const (independent of V )
i
l
R
A
iave 
Q
t
Q dQ
i  lim

t 0 t
dt
V
Ohm ' s Law :
 Const
i
V
 R,
i
where R is resistance
Resistance does not vary with the applied voltage
resistor
Volts
R 

Ampere
Experimentally it is found that R depends on the material
the wire is made of and its dimensions. Does not depend
on the shape.
l
R
A
l is length,
A is the area
 is resistivit y

1

is conductivity
In a wire of uniform resistivity and cross sectional area,
the electric field is a constant for constant currents.
V
+
-
i
V VA 1 VA
i 


R
l 
l
  i 
Exercise 1
8
10
Given the resistivity of copper, about
Ohm-m, what
length of 0.5 cm diameter wire will yield a resistance of 10
Ohms?
Current Density
 
i   j  dS
S
Consider current flowing in a homogeneous wire with cross sectional
area A.
 
i   j  dS   jdS  j  dS  jA
A
A
i
j
A
A
The Continuity Equation for Steady
State Currents
Currents and current densities
are constant in time –

steady state. The flux of j out of any closed
surface must be zero.
 
 j  dS  0
Another form of Ohm’s Law


j  E


E  j
For steady state situation
 
j

d
S

0

 
 E dr  0
Problem 4
Two wires having different resistivities ρ1 and ρ2 and
equal cross sections, a, are connected end to end. Their
lengths are l1 and l2. If a battery is connected to this
system such that a potential difference of V is
maintained between the ends,
a) What will be the current densities in the wires?
b) What will be the potential difference across each wire?
c) Will there be any charge on the surface where the wires
are connected?
Exercise 5
Consider a cylindrical shell, inner radius a and outer radius
b. It is made of material with resistivity ρ. Suppose a current
can be made to flow out from the inner surface to the outer.
What would the resistance be for this current?
Have a great day!