* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download x – 1
Dessin d'enfant wikipedia , lookup
Multilateration wikipedia , lookup
History of trigonometry wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Perceived visual angle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
Rational trigonometry wikipedia , lookup
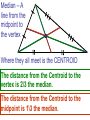
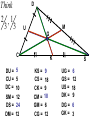
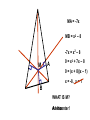
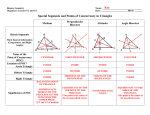
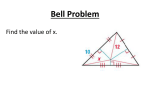
10-3 Concurrent Lines Thrm: Bisectors of the angles of a triangle intersect in a point that is equidistant from the three sides of a triangle. Where multiple lines meet is called the point of concurrency. The lines that go through that point are called concurrent lines. The point of concurrency of angle bisectors is called an INCENTER Justification, points on angle bisector are equidistant to the sides, then transitive. Thrm: Perpendicular bisectors of the sides of a triangle intersect in a point that is equidistant to all the vertices. The point of concurrency of perpendicular bisectors is called a CIRCUMCENTER Justification, points on perpendicular bisector are equidistant to the endpoints, then transitive. So to help keep track of things, it’s like the go with the other, angle bisectors equidistant to sides. Perpendicular bisectors equidistant to vertices. Median – A line from the midpoint to the vertex Where they all meet is the CENTROID The distance from the Centroid to the vertex is 2\3 the median. The distance from the Centroid to the midpoint is 1\3 the median. Thrm: Altitudes all meet at point. Nothing special about it. The point of concurrency of altitudes is called an ORTHOCENTER Think 2 ,1 3 3 D M U G C DU = 5 CU = 5 DC = 10 SM = 12 DS = 24 DM = 12 K KS = CS = CK = CM = GM = CG = 9 18 9 18 6 12 S UG = GS = US = DK = 6 12 18 9 DG = 6 GK = 3 MA = -7x MB = x2 – 8 -7x = x2 – 8 M A 0 = x2 + 7x – 8 0 = (x + 8)(x – 1) x = -8, x = 1 B WHAT IS M? A letter. An incenter! • HW #19: Pg 388: CE 1-3, WE 1-5, 8-16 • There are number style problems that can show up on a test.