Download KAY174 MATHEMATICS

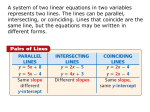
KAY174
MATHEMATICS
II
Prof. Dr. Doğan Nadi Leblebici
APPLICATIONS OF EQUATIONS AND
INEQUALITIES
PURPOSE: TO LEARN HOW TO TRANSLATE RELATIONSHIPS STATED IN THE
PROBLEMS INTO MATHEMATICAL SYMBOLS WHICH IS CALLED “MODELING”.
SOME BUSINESS TERMS
FIXED COST (OVERHEAD) is the sum of all costs that are independent of the level of
production, such as rent, insurance, etc.
VARIABLE COST is the sum of all costs that are dependent on the level of output,
such as labor and material.
TOTAL COST is the sum of variable cost and fixed cost.
Total Cost = Variable Cost + Fixed Cost
TOTAL REVENUE is the price per unit of output times the number of units sold.
Total Revenue = (Price per unit)(Number of units sold)
PROFIT is total revenue minus total cost.
Profit = Total Revenue – Total Cost
EXAMPLE
Problem:
The Kurek Plastic Inc. prouces Product G for which the variable cost per unit is
TL 6 and fix cost is TL 80.000. Each unit has a selling price of TL 10. Determine
the number of units that must be sold for the company to earn a profit of TL
60.000.
Solution:
Profit = Total Revenue – Total Cost; n=units sold
Total Revenue = (Price per unit)(Number of units sold)
Total Cost = Variable Cost + Fixed Cost
60.000=10n-(6n+80.000) → 60.000=10n-6n-80.000
4n=140.000
n=35.000
EXAMPLE
Problem:
A company manufactures women sportswear and is planning to sell its new
model of sportswear set to retail outlets. The cost to the retailer will be TL 33
per set. As convenience to the retailer, the manufacturer will attach a price tag
to each set. What amount should be marked on the price tag so that the
retailer may reduce this price by 20 percent during a sale and still make a
profit of 15 percent on the cost?
Solution:
Selling Price = Cost Per Set + Profit Per Set; p=the tag price
Selling Price = p - .2p
P - .2p = 33 + (.15).(33)
.8p = 37.95
p = 47.4375 → 47.44
EXAMPLE
Problem:
A total of TL 10.000 was invested in two business ventures, A and B. At the end
of the first year, A and B yielded returns of 6 percent and 5 34 percent,
respectively, on the original investments. How was the original amount
allocated if the total amount earned was TL 588.75?
Solution:
Amount invested in A = x and amount invested in B = 10.000 – x
(.06)x + (.0575)(10.000 – x) = 588.75
.06x + 575 – .0575x = 588.75
.0025x = 13.75
x = 5.500
Amount invested in A = 5.500 and amount invested in B = 4.500
LINEAR INEQUALITIES
Suppose a and b are two points on the real number line. Then either a and b
coincide, or a lies to the left of b, or a lies to the right of b.
a
a
b
b
a
b
a b
ba
ab
bb
a b
ba
Another inequality symbol “≤” is read as “less than or equal” and thus symbol
“≥” is read as “greater than or equal”.
An inequality is a statement that one number is less than another number.
LINEAR INEQUALITIES
RULES
If a<b, then a(+/-)c<b(+/-)c
If a<b and c>0, then a/c<b/c
If a<b and c>0, then a(-c)>b(-c) and
a
b

c c
If a<b and a=c, then c<b
If a>b>0 and n>0, then
an  bn
and
n
a n b
LINEAR INEQUALITIES
A linear inequality in the variable x is an inequality which can be written in the
form
ax + b < 0 or ax + b ≤ 0
Examples:
5
2(x – 3)<4 → 2x – 6 <4 → 2x<10 → x<5
3 – 2x≤6 → -2x≤3 → x≥-3/2
-3/2
2(x – 4) – 3 > 2x – 1 → 2x – 8 – 3>2x – 1 → -11>-1 → No solution Φ
LINEAR INEQUALITIES
If a≤x≤b, it is called a closed interval. For closed interval we use [-------]
If a<x<b, it is called a open interval. For open interval we use (--------)
(a,b] means a<x≤b
[a,b) means a≤x<b
[a,∞) means x≥a
(a,∞) means x>a
(-∞,a] means x≤a
(-∞,a) means x<a
(-∞,∞) means -∞<∞
APPLICATIONS OF INEQUALITIES
Problem:
For a manufacturer of thermostats, the combined cost for labor and material is
TL 4 per thermostat. Fixed cost are TL 60.000. If the selling price of a
thermostat is TL 7, how many must be sold for the company to earn profit?
Solution:
Number of thermostat that must be sold = n.
Total cost of thermostat that must be sold = 4n + 60.000
Total revenue of thermostat that must be sold = 7n
Profit = Total Revenue - Total Cost → 7n – (4n + 60.000)>0
3n>60.000
n>20.000
Number of thermostat that must be sold is 20.001
APPLICATIONS OF INEQUALITIES
Problem:
A publishing company finds that the cost of publishing each copy of a certain
magazine is TL 0.38. The revenue from dealers is TL 0,35 per copy. The
advertising revenue is 10 percent of the revenue received from dealers for all
copies sold beyond 10.000. What is the least number of copies which must be
sold so as to have a profit for the company?
Solution:
Number of copies that must be sold = x.
The revenue from dealers = .35x + (.10)[(.35)(x-10.000)]
Profit = Total Revenue - Total Cost → .35x + (.10)[(.35)(x-10.000)] -.38x>0
.35x + .035x-350 -.38x>0
.005x – 350>0
x>70.000
Number of copies that must be sold is 70.001
ABSOLUTE VALUE
Sometimes it is useful to consider, on the real number line, the
distance between a number x and 0. We call this distance the
absolute value of x and denote it by IxI. For example, I5I=5 and I5I=5 because both 5 and -5 are five units from 0. Similarly I0I=0.
Example
Ix-3I=2
x-3=2 or x-3=-2 → x=5 or x=1
I7-3xI=5
7-3x=5 or 7-3x=-5 → x=4 or x=2/3
FUNCTIONS AND GRAPHS
PURPOSE: TO UNDERSTAND RELATIONSHIP BETWEEN DEPENDENT AND
INDEPENDENT VARIABLES IN A FORMULA.
FUNCTIONS
In 1964, Leibniz, one of the developers of calculus, introduced the
word function into the mathematical vocabulary.
A function is a rule that assigns to each input number exactly one
output number. The set of all input numbers to which the rule
applies is called the domain of the function. The set of all output
numbers is called the range.
y = x + 2 For each value of x, there is a value for y.
x is independent variable and y is dependent variable.
FUNCTIONS
Examples
y2=x Let’s say x=9 → y2=9 → y=±3
Thus y has two values, -3 and 3. Hence y is not a function of x.
x=y2
Let’s say y=3 → x=9 → Hence x is a function of y.
Suppose that the equation p=100/q describes the relationship
between the price per unit, p, of a certain product and the
number of units, q, of that product that consumers will buy (that
is, demand) per week. This equation is called demand equation
for the product. If q is an input number, then to each value of q
there is assigned exactly one output number p.
FUNCTIONS
Examples
q→100/q=p
20→100/20=5
Thus price is a function of quantity demanded. Since q can not be
0 or negative, domain is all values of q such that q>0.
f(q)=100/q → f(q)=p
f(5)=100/5 → f(5)=20 → p=20
FUNCTIONS
f(x)=2 is a constant function.
y=f(x)=-3x2 + x -5 is a quadratic function.
y=f(x)=-cnxn + cn-1xn-1 + c1x + c0 is a polynomial function. cn is the
leading coefficient. n is called the degree of function.
f(x)=IxI is an absolute value function.
COMBINATIONS OF FUNCTIONS
If f and g are functions, we can combine them to create new
functions. For example,
f(x)=x2 and g(x)=x + 1
Adding f(x) and g(x) in the obvious way gives
f(x) + g(x) = x2 + (x + 1)
This sum defines a new function – Let’s call it H
H(x)=f(x) + g(x) = x2 + (x + 1)
GRAPHS IN RECTANGULAR COORDINATES
A rectangular (or Cartesian) coordinate system allows us to
specify and locate points in a plane. It also provides a geometric
way to represent equations in two variables as well as functions.
GRAPHS IN RECTANGULAR COORDINATES
Using a rectangular coordinate system, we can geometrically
represent equations in two variables. For example;
y = x2 + 2x -3
GRAPHS IN RECTANGULAR COORDINATES
Example
y = 2x + 3
GRAPHS IN RECTANGULAR COORDINATES
Example
s = 100/t
GRAPHS IN RECTANGULAR COORDINATES
Example
x = 2y2
LINES, PARABOLAS, AND SYSTEMS
PURPOSE: TO LEARN THE STEEPNESS TO INTERPRET RELATIONSHIP IN
ECONOMICS.
LINES
To measure the steepness of a line we introduce the notion of
slope (m).
Change(in ) y
Slope 
Change(in ) x
Example
Suppose that the line below shows the relationship between the
price p of a widget (in TL) and the quantity q of widgets (in
thousands) that consumers will buy at that price. Find and
interpret the slope.
LINES
Example
We can use slope formula:
p2  p1
Slope  m 
q2  q1
1 4
3
m

62
4
The slope is negative, -3/4. This means that for each increase in
quantity of 1 (thousand widgets), there corresponds a decrease
in price of ¾ (TL per widget). Due to this decrease the line falls
from left to right.
LINES
y – y1 = m(x – x1) is the point-slope form of an equation of line
through (x1,y1) and having slope m.
Y = mx – b is the slope-intercept form of an equation of line with
slope m and y-intercept (0,b).
A function f is a linear function if and only if f(x) can be written in
the form f(x) = ax + b, where a and b are constants and a ≠ 0.
PARABOLAS
The graph of the quadratic function y = f(x) = ax2 + bx + c is called
a parabola and has a shape such as the curves below. Vertex
occurs at (-b/2a, f(-b/2a)).
PARABOLAS
Example
Suppose the demand function for a manufacturer’s product is
p=f(q)=1000-2q, where p is the price (in TL) per unit when q units
are demanded (per week) by consumers. Find the level of
production that will maximize the manufacturer’s total revenue,
and determine this revenue.
Solution
Total Revenue=(Price)(Quantity)
r=(1000-2q)q → r=1000q -2q2→ r is a quadratic formula
a=-2, b=1000, c=0 → q=-b/2a maximum (vertex)
q=-1000/2(-2)=250 → r=125.000
PARABOLAS
Solution
Total Revenue=(Price)(Quantity)
r=(1000-2q)q → r=1000q -2q2→ r is a quadratic formula
a=-2, b=1000, c=0 → q=-b/2a maximum (vertex)
q=-1000/2(-2)=250 → r=125.000
SYSTEMS OF LINEAR EQUATIONS
We sometimes have to solve two equations that all equations in
the set are satisfied simultaneously.
For example; suppose that a company pays its salespeople on the
basis of a certain percentage of the first TL 100.000 in sales, plus
a certain percentage of any sales beyond TL 100.000. If a
salesperson earned TL 17.000 on sales of TL 300.000 and another
earned TL 12.500 on sales of TL 225.000, what are the two rates?
x = rate for first 100.000 and y = rate for sales beyond 100.000
100.000x + 200.000y = 17.000
100.000x + 125.000y = 12.500
SYSTEMS OF LINEAR/NONLINEAR EQUATIONS
The set of linear equations
 a1 x  b1 y  c1

a2 x  b2 y  c2
İs called a system of two linear equations in the variables (or
unknowns) x and y. Its solution consists of values of x and y
which satisfy both equations simultaneously.
100.000 x  200.000 y  17.000

100.000 x  125.000 y  12.500
SYSTEMS OF LINEAR/NON LINEAR EQUATIONS
100.000 x  200.000 y  17.000

100.000 x  125.000 y  12.500
The left and right sides of equations can be substracted from the
corresponding side of equations.
100.000x + 200.000y – (100.000x + 125.000y) = 17.000 – 12.500
75.000y = 4500
y = .06 and x = .05
Formulas in system can be nonlinear also. Solution of such systems
should also satisfy both equations simultaneously.
SYSTEMS OF LINEAR/NON LINEAR EQUATIONS
Example
1

 p   180 q  12,

1
 p
q 8
300

SYSTEMS OF LINEAR/NON LINEAR EQUATIONS
Example
1

 p   180 q  12,

1
 p
q 8
300

1
1
q 8  
q  12
300
180
q  450
1
p
(450)  8
300
p  9.50