* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 4.2 Some Ways to Prove Triangles Congruent
Penrose tiling wikipedia , lookup
Rational trigonometry wikipedia , lookup
Technical drawing wikipedia , lookup
Multilateration wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
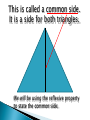
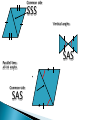
1. If two triangles are congruent, then they have matching________ and ________. 2. Complete the congruence statement. 1. T 2. m I 3. CA 4. IG 5. ΔATC 6. ΔBGI 7. E, F, S, T 8. Definition of Δs 9. L F, X N, R E, LX FN, XR NE, LR FE 10.a. ΔKRO b. K, CPCT c. KO, CPCT d. R, CPCT Alt Int s are 11.a. ΔRLA b. RL c. 3, CPCT LR, Alt Int s are d. 4, CPCT PL, AR, Alt Int s are Section 4-2 Some Ways to Prove Triangles Congruent When we talk about congruent triangles, we mean everything about them is congruent. All 3 pairs of corresponding angles are equal…. And all 3 pairs of corresponding sides are equal For us to prove that 2 people are identical twins, we don’t need to show that all “2000” body parts are equal. We can take a short cut and show 3 or 4 things are equal such as their face, age and height. If these are the same I think we can agree they are twins. The same is true for triangles. We don’t need to prove all 6 corresponding parts are congruent. We have 5 short cuts or methods. Today we will look at 3 methods. SSS If we can show all 3 pairs of corresponding sides are congruent, then the triangles are congruent. SAS If we can show 2 pairs of sides and the included angles are congruent, then the triangles are congruent. Included angle Non-included angles This is called a common side. It is a side for both triangles. We will be using the reflexive property to state the common side. If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent. M Y N Z L X XYZ ~= LMN by ASA Post. Vertical Angles are ≅ Angles pairs formed when two lines are parallel. ◦ Alternate Interior Angles Which method can be used to prove the triangles are congruent? Common side SSS Vertical angles Parallel lines alt int angles Common side SAS SAS Tick Mark Common Side Yes ≅ by SAS Tick Mark Common Side NOT ≅ Tick Mark Common Side Yes ≅ by SSS || Lines-Alt Int. ∠𝑠 ≅ Common Side Yes ≅ by SAS Common Side Yes ≅ by ASA You must use theorems, postulates, and definitions to deduce sides/angles are congruent. “It looks the same” will not suffice. T Given: E is the midpoint of MJ; TE ⊥ MJ M Prove: ∆𝑀𝐸𝑇 ≅ ∆𝐽𝐸𝑇 E Statements Reasons 1. E is the midpt. of MJ. 1. Given. 2. 𝑀𝐸 ≅ 𝐸𝐽 2. Def. of midpt. 3. TE ⊥ MJ 3. Given 4. ∠𝑀𝐸𝑇 ≅ ∠𝐽𝐸𝑇 5. TE=TE 4. If two lines are ⊥, then they form ≅ adj. ∠s 5. Reflexive Prop. 6. ∆𝑀𝐸𝑇 ≅ ∆𝐽𝐸𝑇 6. SAS Postulate J Pg 124-126 Written Exercises #1-17 All