* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Finding the Equation of a Line
Line (geometry) wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Recurrence relation wikipedia , lookup
Location arithmetic wikipedia , lookup
System of polynomial equations wikipedia , lookup
Elementary algebra wikipedia , lookup
Partial differential equation wikipedia , lookup
Lesson 2 Exponent Rules
Definitions:
Def: an = a•a•…•a
n times
Def: a0 = 1, if a≠0
Def: a-n =
𝟏
𝟏
𝒂
𝒂−𝒏
𝒏,
Properties:
1) aman = am+n
2)
𝒂𝒎
𝒂𝒏
=a
m-n
3) (am)n = amn
4) (ab)m = ambm
= an, if a≠0
ex. 23•22 =
ex.
𝟐𝟑
𝟐𝟓
=
ex. (23)2 =
Ex. Simplify:
𝒏𝟎 𝒑−𝟐 (𝒂𝒏𝟐 )−𝟑
𝟐𝒑𝒑𝟐 (𝒂−𝟑 )𝟎 𝒂−𝟐
factors to the 0 power = 1
multiply outer exponent
move terms with negative exp
multiply by adding exp
divide by subtracting exp
Ex. Simplify:
𝟑𝒃−𝟐 𝒒𝒄𝟑 (𝒃−𝟑 )−𝟐
(𝟐𝒒𝟎 𝒃)𝟑 (𝒄−𝟑 )
Ex. Simplify:
(𝒏𝟐 )−𝟐 𝒌𝒎𝟎 𝒏𝟑
(𝟐𝟎 𝒌−𝟐 𝒎)𝟐 𝒏−𝟑 𝒏
Lesson 3 Evaluating Formulas,
Adding Like Terms
Evaluating:
Ex. Evaluate a2b – ab2 if a = -3 and b = 2
Ex. Evaluate (ab – a2b) – b if a = 2 and b = -5
Adding Like Terms:
Ex. Simplify by combining like terms:
−𝟏 𝟐
−𝟏
−𝟐 𝟐 −𝟏 −𝟑
𝟐𝒂
𝒑
𝒌
𝟑𝒑
𝒌
𝟓𝒑
𝒑 𝒂 𝒌
𝒂𝒌𝟑 𝒑−𝟐 +
−
+
𝒌𝟒
𝒂−𝟏 𝒑𝒌−𝟐
𝒑−𝟐
simplify each term
combine coefficients
of like terms (those w/
same variables, exp.)
Ex. Simplify by combining like terms:
𝟓𝒃𝟑 𝒒−𝟏 𝒎𝟐 𝟐𝟎 𝒎
𝟐𝒎−𝟐 𝒒
− −𝟐 − −𝟏 𝟐 −𝟑
𝒎𝟑
𝒃
𝒎 𝒒 𝒃
Lesson 4: The Distributive Property, Solving Equations
The Distributive Property: c(a + b) = ca + cb
ex. 5(2 + 3) = 5(2) + 5(3)
ex. Expand:
𝟓𝒑𝒒𝟎 𝟐𝒑−𝟐 𝒎−𝟑 𝒎−𝟐 𝒒𝟑
(
−
)
𝒎−𝟐
𝒒𝟐
𝒑𝟑
distribute
simplify each term
ex. Expand:
𝟐𝒚𝒙−𝟏 𝟑𝟎 𝒚𝟎 𝒌𝒌−𝟏 𝒙𝟐 𝒙𝒌
(
−
)
𝒌𝟐
𝒙
𝒚𝒚𝟑
Solving Equations:
Ex. Solve:
𝟑
𝟓
𝟓
𝟑
𝟐 𝒙+
=
𝟏𝟓
𝟐
𝒙−𝟐
write as improper fractions
multiply both sides of the
equation by the LCD, canceling
denominators
continue to solve
Ex. Solve:
𝟐
𝟏
𝟑
𝟐
− (𝟒 −
𝒙) =
𝟓
𝟔
𝒙+𝟏
Lesson 5 Introduction to Word Problems
Ex. The sum of a number and 5 is multiplied by 7.
The result is 10 less than 2 times the number.
What is the number?
Ex. Two times a number is added to 5 and the sum
is multiplied by 4. The result is 12 more than 6
times the number. What is the number?
Ex. Two fifths of the calculus students preferred
blue notebooks. If 120 students were in calculus,
how many did not prefer blue notebooks?
Lesson 6 Problems with Decimal Numbers,
Consecutive Integer Problems,
Problems with Decimals:
Ex. Solve: .02x - .13 = .6x + 3.1
Multiply both sides
by 100
Solve
Ex. Luella found that a honey bee perched on
0.013 of the Dandelions examined. If 10,000
Dandelions were examined, how many did not
have a honey bee?
Consecutive Integer Problems:
Integers: …-3, -2, -1, 0, 1, 2, 3…
Consecutive Odd Integers: …-5, -3, -1, 0, 1, 3, 5…
Consecutive Even Integers: …-6, -4, -2, 0, 2, 4, 6…
For variables:
Consecutive Integers: x, x + 1, x + 2, …
Consecutive Even/Odd Integers: x, x + 2, x + 4,…
Ex. Find three consecutive odd integers such that
two times the sum of the first and the third is 17
less than 5 times the second.
Ex. Find three consecutive integers such that
three times the sum of the second and third is four
less than five times the second.
Lesson 7: Percentage Word Problems
Recall: 60% = 0.60, 13% = 0.13, 1.5% = .015
Ex. Twenty-four is eighty percent of what
number?
Ex. Fourty-nine hundred is what percent of seven
hundred?
Lesson 8 Graphing Linear Equations
Ex. Graph 2x + 3y = 6
x y
Slopes of Lines: m =
𝒓𝒊𝒔𝒆
𝒓𝒖𝒏
=+
𝒖𝒑
𝒓𝒊𝒈𝒉𝒕
=−
𝒅𝒐𝒘𝒏
𝒓𝒊𝒈𝒉𝒕
Slope intercept form: y = mx + b
m = slope, b = y intercept
Ex. Graph 3x – 2y = 10
Lesson 9 More Percent Word Problems
Ex. Seventy percent of the Algebra students
handed in their homework on Monday. If sixty
Algebra students did not hand in their homework
on Monday, how many Algebra students were
there?
Ex. The Beekeeper was astounded because this
year’s honey production increased by 150%. If
she harvested 750 pounds of honey this year, how
many pounds did she harvest last year?
Lesson 10 Distance and the Pythagorean Theorem
Recall the Pythagorean Theorem:
In a right triangle with legs of length a and b and
hypotenuse of length c,
c
b
a
a2 + b2 = c2
Ex. Find a:
9
11
a
Ex. Use the Pythagorean Theorem to find the
distance between (-3, 2) and (5, -1).
Lesson 11 Addition of Rational Expressions
Fractions must have the same denominator in
order to be added or subtracted.
Ex. Add
𝟏
𝟏𝟐
+
𝟑
𝟏𝟎
Find the LCD
Use the
Numerator/Denominator
rule to get the LCD
Add the numerators over
the LCD
Ex. Add
𝟏
𝟐𝟒
+
𝟏
𝟏𝟖
Ex. Add
𝒙
𝟐𝒃𝟐
+
𝒂𝒌
𝒃𝒎
+ 𝒚
Ex. Add
𝒂𝒃
𝟐𝒄
+ 𝟑+
𝒂𝟐
𝒄𝟐 𝒅𝟑
Ex. Add
𝒋𝒙
𝟓𝒌𝒏𝟑
+
𝒎
𝒌𝒏
+
𝒚
𝒏𝟐
Lesson 12: Finding the Equation of a Line From its
Graph
Recall
Slopes of Lines: m =
𝒓𝒊𝒔𝒆
𝒓𝒖𝒏
=+
𝒖𝒑
𝒓𝒊𝒈𝒉𝒕
=−
𝒅𝒐𝒘𝒏
𝒓𝒊𝒈𝒉𝒕
Slope intercept form: y = mx + b
m = slope, b = y intercept
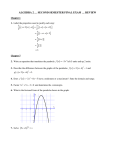
Ex. Find the equation of the line below:
Ex. Find the equation of the line below:
Ex. Find the equation of the line below:
Ex. Find the equation of the line below:
Lesson 13 Solving Systems of Equations
Using Substitution
Ex. Use substitution to solve:
x = 2y – 3
3x + 5y = 24
Ex. Use substitution to solve:
3x + 2y = 15
5x + y = -10
Lesson 14: Finding the Equation of a Line
Ex. Find the equation of the line passing through
the points (2, -3) and (-1, 7)
Graph the line
Calculate slope from graph
Insert (x,y) and m into
y = mx + b and use algebra
to find b.
Ex. Find the equation of the line passing through
(-2, 6) with slope -2/5.
Lesson 15: Solving Systems of Equations Using
Elimination:
Ex. Solve: -3x + y = 11
3x – 2y = 2
Add the equations to
eliminate x, Solve
Find x
Ex. Use elimination to solve:
3x – 2y = 22
5x + 3y = 5
Multiply each equation so that the y (or x) coefficients are opposites.
Then add the equations to eliminate a variable and solve.
3x – 2y = 22
5x + 3y = 5
Ex. Solve using elimination:
-2x + 5y = 19
3x + 4y = 6
Lesson 16 Multiplication and Division of
Polynomials
Multiplication:
Ex. Multiply: (3x + 2)(5x2 – x + 4)
Division:
First consider long division of numbers:
232 ÷ 11 =
𝟐𝟑𝟐
𝟏𝟏
̅̅̅̅̅̅
= 𝟏𝟏|𝟐𝟑𝟐
1) Divide to choose what to multiply by (first terms)
2) Multiply (both terms)
3) Subtract
4) Bring Down
5) Repeat
Ex. Divide 3 – 2x + 5x2 + 2x3 by -2 + x
Check:
(x – 2)(2x2 + 9x + 16) + 35
2x3 + 9x2 + 16x – 4x2 – 18x – 32 + 35
2x3 + 5x2 - 2x + 3
Ex. Divide x3 + 2x + 7 by -2 + x
Ex. Divide -2 + 3x – 4x2 – 2x3 by -1 + x
Lesson 17: Subscripted Variables
Ex. Solve: RBTB + RGTG = 240, RB = 40, RG = 60,
TB + TG = 8
Ex. Solve: RJTJ + RCTC = 1000, RJ = 60, RC = 50,
TJ + TC = 16
Lesson 18 Ratio Word Problems
Ex. At the kennel club, the ratio of mixed breed
dogs to pure bred dogs was 7 to 3. If there were
120 dogs at the kennel club, how many were pure
bred?
Given:
Unstated:
The question regards which two quantities?
Ex. It took 2 cups of chocolate chips to mix 8 cups
of cookie dough. How many cups of other
ingredients are required to mix 28 cups of cookie
dough?
Given:
Unstated:
The question regards which two quantities?
Ex. It took 300 kg of lead to make 5000 kg of the
new compound. How many kg of other materials
are required to make 12000 kg of the new
compound?
Lesson 19: Word Problems With Items of Value
Ex. There were thirty-three dimes and quarters in
all whose value was six dollars and thirty cents.
How many were dimes and how many were
quarters?
Number of items:
Value of items:
Ex. Adult tickets cost twenty dollars each while
children’s tickets cost only fifteen dollars each. If
Bruce bought a total of fifteen tickets and spent
$260.00, how many children’s tickets did he buy?
Lesson 20: Introduction to Radicals, Parallel Lines
Radicals:
Consider:
√𝟒 = 𝟐 because 2•2 = 4
Also √𝟐 ≈ 𝟏. 𝟒𝟏𝟒
√𝟐√𝟐 = 2
However, 1.414 • 1.414 = 1.999396
Similarly, √𝟓 ≈ 𝟐. 𝟐𝟑𝟔
√𝟓√𝟓 = 𝟓
However, 2.236 • 2.236 = 4.999696
A square root equals that number which multiplied
times itself equals the radicand.
We will only consider the principal, or positive,
root.
Ex. Simplify: √𝟓𝟎𝟎
find the prime factorization
of 500
a square root times itself
equals the radicand
Ex. Simplify √𝟕𝟐
Ex. Simplify:
𝟑√𝟏𝟓𝟎 − 𝟓√𝟐𝟏𝟔
simplify each term
only like terms may be
added or subtracted
Ex. Simplify 𝟐√𝟑(𝟑√𝟑 − 𝟓√𝟏𝟐)
distribute, coefficients
multiply, radicands
multiply
simplify each term
Ex. Simplify 𝟐√𝟑 ∙ 𝟒√𝟏𝟖 − 𝟔√𝟐𝟎𝟎
Parallel Lines:
The slopes of parallel lines are equal.
Ex. Find the equation of a line parallel to
2x – 3y = 6 which passes through the point (-1, 2).
solve the given equation
for y, find its slope
fill in m, (x,y) into y = mx + b
and use algebra to find b
Ex. Find the equation of the line parallel to
3x – 2y = 12 which passes through (-2, 4)
Lesson 21: Scientific Notation, Word Problems
With Two Equations and Two Variables
Scientific Notation:
Very small numbers: 0.00034 = 3.4 x 10-4
𝟏
= 3.4 x
= 3.4 x
𝟏𝟎𝟒
𝟏
𝟏𝟎,𝟎𝟎𝟎
Very large numbers: 3,200,000 = 3.2 x 106
= 3.2 x 1,000,000
A number in proper scientific notation has one
digit to the left of the decimal.
Ex. Simplify:
𝟐𝟎𝟎𝟎 × 𝟏𝟎−𝟐
𝟗𝟎𝟎𝟎
∙
𝟎.𝟎𝟎𝟎𝟏𝟖 × 𝟏𝟎𝟑
𝟎.𝟐𝟎𝟎𝟎𝟎
write each number in
proper scientific notation
make a separate fraction
out of the powers of ten
use exponent rules to
simplify the fraction
Word Problems With Two Variables:
Ex. The ratio of two numbers is 3 to 7. Their sum
is 120. What are the two numbers?
Ex. The sum of two numbers is 81. Their
difference is 35. What are the two numbers?
Lesson 22: Introduction to Uniform Motion
Problems
Recall: D = R∙T
for example, 600 miles = 60 mph ∙10 hr.
For this lessons problems, two distances will be
equal.
Identify Distance, Rate and Time with capital D, R
and T. Use subscripts to indicate which individual
the distance, rate or time is associated with. For
example, distance for Julie: DJ
Ex. Victoria made the trip to Grandmother’s in 10
hours. It took her brother Michael just 8 hours to
make the same trip because his speedometer was
broken. If Victoria was traveling at 50 mph, how
fast was Michael traveling?
draw arrows to represent
distances traveled
make an equation relating
distances
replace each distance with
the equivalent rate ∙ time
fill in the known values
solve
Ex. On the way to Springfield, Jon’s Piper flew at just
200 mph into the wind but on the way back he caught a
tail wind and traveled at 250 mph. If the total traveling
time was 9 hours, how far was it to Springfield?
Lesson 23: Solving Systems of Equations by
Graphing
Ex. Find the solution by graphing:
2x + y = 3
y = -3x + 6
graph each line
the intersection is the
solution
check your answer
Lesson 24: Equations With Fractions
Ex. Solve:
𝟑𝒙−𝟏
𝟒
−
𝟓
𝟔
=
𝟏
𝟑
use prime factorization
to find LCD
multiply both sides
of the equation by LCD,
canceling denominators
solve
Ex. Solve:
𝟐𝒙
𝟓
−
𝟔+𝟑𝒙
𝟏𝟎
=𝟒
Lesson 25 Factoring the GCF, Cancellation
Factoring the GCF:
Ex. Factor:
16x3yz2 – 8x2y3z3 + 4xyz2
Cancellation:
Do not cancel part of a sum or a difference. Sums
and differences must completely cancel or not
cancel at all.
Ex. Simplify:
(𝟓)(𝟑𝟒)
(𝟓)
can cancel a
factor in a product
Ex. Simplify:
𝒙+𝟓
𝟓
can’t cancel part
of a sum
Ex. Simplify
Ex. Simplify:
𝟓𝒙+𝟓
𝟓
factor and then cancel
𝟏𝟐𝒚𝟑 − 𝟒𝒚
𝟒𝒚
Ex. Simplify:
𝟐𝟕𝒂𝟒 − 𝟏𝟐𝒂𝟐
𝟑𝒂𝟐
Lesson 26: Factoring Trinomials x2 + bx + c
Recall: Multiplication:
(x + 3)(x – 2)
F:
O:
I:
L:
Firsts
Outers
Inners
Lasts
Thus, factoring requires two numbers whose
product is the constant and whose sum is the x
coefficient.
Ex. Factor: x2 + 3x – 10
product = -10, sum = 3?
Ex. Factor: -x2 – x + 56
factor out -1
(-1 remains in final answer)
product = -56, sum = 1?
Ex. Factor: -10x2 + x3 + 16x
factor off GCF,
write in descending order
Lesson 27 Rational Expressions Whose
Denominators Contain Sums
Recall: Rational Expressions must have the same
denominators before they can be added or
subtracted.
Check denominators to see if they factor.
A sum in a denominator is a distinct factor in the
LCD.
Ex. Add
𝒙+𝟐
𝒙−𝟏
+ 𝟑−
𝟒
𝒙𝟐
Find LCD
Each fraction needs to
have the LCD
Combine numerators
over LCD
Ex. Add:
𝟑
𝒂+𝟐
−
𝟒
𝒂
Ex. Add:
𝒎−𝟏
𝒎𝟐 + 𝒎−𝟔
+
𝟑
𝒎(𝒎−𝟐)
Lesson 28: Complex Fractions, Introduction to
Rationalizing Denominators
Complex Fractions:
Recall:
𝟑
𝟓
𝟏
𝟕
=
𝟑
𝟓
∙
𝟕
𝟏
=
𝟐𝟏
𝟓
Invert (flip) and multiply the bottom fraction times
the top fraction.
Ex. Simplify:
𝒙
𝒚
𝒙+𝟑
𝒚
Ex. Simplify:
𝒂
𝒃−𝒄
𝒅
𝒃−𝒄
Introduction to Rationalizing Denominators:
Do not leave radicals (roots) in the denominator.
Multiply the numerator and the denominator by the
square root in the denominator.
Ex. Simplify:
Notice that
𝟔
𝟓√𝟑
𝟔
𝟓√𝟑
≈ . 𝟔𝟗𝟐𝟖 and
𝟐√𝟑
𝟓
≈ . 𝟔𝟗𝟐𝟖
Ex. Simplify:
10
7√2
Lesson 29: Uniform Motion Problems in Which the
Sum of Two Distances is Known
Recall:
At first:
D1 = D2
R1T1 = R2T2
Now we will also see,
D1 + D2 = k
R1T1 + R2T2 = k
Ex. Bruce and Wendy parted at O’Hare
International Airport when Wendy’s plane left at
9:00 am. flying East at 350 mph. Bruce’s plane
sped West at 300 mph but did not leave until 11:00
am. What time was it when the two were 2000
miles apart?
draw arrows
representing distance
distances add to 2000
replace each distance
with corresponding
rate x time
fill in known values
make a 2nd equation
regarding times
solve
answer the question
Ex. Scarlett rode in the wagon at 5 mph for part of
the 40 mile trip to Tara until her horse became
worn out and she had to walk the remaining
distance at 3 mph. If the total trip took 10 hours,
how far did she walk?
Lesson 31: Perpendicular Lines
Perpendicular lines form a right angle.
The slopes of perpendicular lines are opposite
reciprocals:
ex. -2,
𝟑
𝟓
,−
𝟏
𝟐
𝟓
𝟑
𝟕 𝟒
− ,
𝟒 𝟕
Ex. Find the equation of the line perpendicular to
the line 2x – 3y = 12 passing through the point
(-2, 1).
solve for y and find the
slope of the given line
find the perpendicular
slope
fill m, (x, y) into y = mx + b
and solve for b
write the equation of the
line
Ex. Find the equation of the line perpendicular to
the line 3x – 4y = 8 passing through the point
(1, -3).
Lesson 32: Combining Roots Containing Fractions
𝟑
𝟕
𝟕
𝟑
Ex. Simplify: √ + √
make individual roots in the
numerator & denominator
rationalize the denominator
need LCD in both terms
add like terms
Ex. Simplify:
𝟑
𝟐
𝟐
𝟑
𝟑√ − 𝟒√
Ex. Simplify:
𝟐
𝟓
𝟓
𝟐
𝟐√ − 𝟑√
Lesson 33: Complex Fractions Containing Sums
First we combine fractions to attain a single
fraction in the numerator and a single fraction in
the denominator. Then invert and multiply the
denominator.
Ex. Simplify:
𝒙
𝟐
+
𝒚 𝟑𝒚
𝟐
𝒚
“little fractions” in the
numerator need to have
the same LCD to add
add “little fractions”
invert and multiply denominator
reduce (cancel) if possible,
remember, don’t cancel part
of a sum
Ex. Simplify:
𝟑𝒂𝒃
+𝟐
𝒄
𝟏 𝒃
+
𝒄 𝟑𝒄
Ex. Simplify:
𝒋
𝟏
+
𝒌+𝟑 𝒌
𝟓
𝒋+𝒏
Lesson 34: Uniform Motion Problems in Which
One Distance is Shorter than the Other
First,
D1 = D2
R1T1 = R2T2
Then,
D1 + D2 = k
R1T1 + R2T2 = k
Now we will also see,
D1 + k = D2
R1T1 + k = R2T2
Ex. Jack and Jill raced up the hill. In 50 seconds,
Jill reached the top. She turned just in time to see
Jack fall down only 100 m from the top. If Jill ran
at 8 meters per second, how fast was Jack
running before he fell?
Ex. Jack had a 45 mile head start and was
traveling at 15 mph when Jill set out to catch him.
If Jill was traveling twice as fast as Jack, how long
did it take for her to catch Jack?
Lesson 35: Rational Exponents
Recall: √𝟐√𝟐 = 𝟐 because √𝟐 is that positive
number which when multiplied times itself yields 2.
𝟑
By √𝒙 we mean that number which when
multiplied times itself 3 times yields x.
𝟑
Ex. √𝟖 = 2 because 2∙2∙2 = 8
𝟑
𝟑
𝟑
Ex. √𝟐 √𝟐 √𝟐 = 𝟐
𝟑
Notice, √𝟐 ≈ 1.414 but √𝟐 ≈ 1.260
𝟑
𝟑
𝟑
Ex. √𝟓 √𝟓 √𝟓 = 𝟓
Radicals may be written using fractional
exponents.
𝟐
Ex. √𝟑 = √𝟑 =
𝟑
𝟏⁄
𝟑 𝟐
𝟏⁄
𝟑
Ex. √𝟓 = 𝟓
𝒏
𝒏
In general, √𝒂𝒎 = ( √𝒂)𝒎 = 𝒂
Ex. Simplify 𝟐𝟕
𝒎⁄
𝒏
−𝟏⁄
𝟑
negative exponents move
factors to the other side of
the fraction
write as a cubed root
simplify the radical
Ex. Simplify:
𝟐⁄
𝟏𝟐𝟓 𝟑
Ex. Simplify:
−𝟐⁄
−𝟔𝟒 𝟑
Lesson 36: Multiplication and Division of Rational
Expressions
Recall:
𝟓
𝟑
𝟕
𝟐
=
𝟓
𝟑
÷
𝟕
𝟐
=
𝟓
𝟑
∙
𝟐
𝟕
=
𝟏𝟎
𝟐𝟏
Divide rational expressions by inverting and
multiplying.
Ex. Simplify:
𝑥 2 − 6𝑥+5
𝑥 2 + 𝑥−2
÷
𝑥 2 − 2𝑥−15
𝑥 2 + 10𝑥+21
invert and multiply
factor and cancel
Ex. Simplify:
𝒙𝟑 − 𝟒𝒙𝟐 − 𝟐𝟏𝒙
𝒙𝟐 + 𝟓𝒙+𝟔
÷
𝒙𝟑 − 𝟖𝒙𝟐 + 𝟕𝒙
𝒙+𝟐
Lesson 38: Powers of Sums, Solving by Factoring
Powers of Sums:
Ex. Expand: (x + 3)3
Solving by Factoring:
Consider:
If 8∙n = 0, then n = 0.
If m∙n = 0, then m = 0 or n = 0 or both
The Zero Factor Principle:
If k∙p∙…∙q = 0
then k = 0 or p = 0…or q = 0
Ex. Solve:
x3 = 3x2 + 28x
need 0 on one side of
the equation
factor
set each factor = 0 and solve
Ex. Solve: 0 = 162 + 3x2 – 45x
Lesson 39: Factoring the Difference of Two
Squares
Consider:
Conjugates: the same two terms with the opposite
middle sign
ex: 2x + 3, 2x – 3
-x + 5, -x – 5
4x – 1, 4x + 1
Consider the product of conjugates:
(2x + 3)(2x – 3) = 4x2 + 6x – 6x – 9 = 4x2 – 9
(-x + 5)(-x – 5) = x2 + 5x – 5x – 25 = x2 – 25
(4x – 1)(4x + 1) = 16x2 + 4x – 4x – 1 = 16x2 – 1
Thus the difference of two squares can be
factored as the product of two conjugates.
Ex. Solve by factoring:
49x2 – 36 = 0
factor the difference of
squares
set each factor = 0
solve
Ex. Solve by factoring:
81x2 – 121 = 0
Lesson 40: Solving an Abstract Equation
Ex. Solve for b:
𝟐+
𝟑
𝒙
= 𝒚𝒛 +
𝒂
𝒃
multiply both sides of the
equation by the LCD to cancel
the denominators
isolate “b” terms on one side
factor “b” off
divide out “b’s” coefficient
Ex. Solve for f:
𝒂
𝒆
𝒄
− 𝟐= +
𝒃
𝒇
𝟓
Ex. Solve for m:
𝒙
𝒚
+ 𝒄=
𝒎
𝒂
Lesson 41: Converting Units
Unit examples: lbs., ft., mi., m, sec.
A unit multiplier is a fraction with equivalent
values in the numerator and denominator but
different units.
Some Unit Multipliers:
𝟏 𝒇𝒕
𝟏𝟐 𝒊𝒏
𝟓𝟐𝟖𝟎 𝒇𝒕
𝟏 𝒎𝒊
𝟏 𝒉𝒓
𝟔𝟎 𝒎𝒊𝒏
𝟏 𝒚𝒅
𝟑 𝒇𝒕
Equal
Equal
Equal
Equal
Each unit multiplier may be written inverted.
We multiply quantities by unit multipliers to cancel
units we do not want and introduce units we do
want.
Ex. Use unit multipliers to convert 35 miles to
inches.
Consider square inches, cubic inches:
1 in.2
1 in.
1 in
1 in.3
1 in.
1 in.
1 in.
Ex. Convert 2 cubic miles to cubic inches.
Ex. Convert 3200 square inches to square feet.
Lesson 45: Introduction to Solving Quadratic
Equations
Consider: Solve:
Ex. Solve:
x2 = 13
x2 = 25
x = 5 or x = -5
take the square root of both
sides of the equation, don’t
forget the ±on the right
Ex. Solve:
(x +
𝟏 2
)
𝟑
= 12
take the square root of both
sides of the equation, don’t
forget the ±on the right
solve for x
simplify
Ex. Solve:
(x + 4)2 = 15
Lesson 46: More on Simplifying Radicals Involving
Fractions, More on Simplifying Radicals Using
Fractional Exponents
Ex. Simplify:
𝟑
𝟕
𝟓√ + 𝟐√ − 𝟑√𝟖𝟒
𝟕
𝟑
make individual roots in the
numerator & denominator
rationalize the
denominators
simplify the √𝟖𝟒
need LCD in each term
add like terms
Ex. Simplify:
𝟐
𝟓
𝟓
𝟐
√ − 𝟑√ − 𝟒√𝟐𝟓𝟎
Recall:
𝒏
√𝒂𝒎
= 𝒂
𝒎
𝒏
Ex. Simplify:
3
5
√𝑎5 𝑏 2 √𝑎3 𝑏
write each factor with rational
exponents
multiply factors with the same
base by adding their exponents
exponents need the same LCD
to be added
Ex. Simplify:
√5√5
write the inner √𝟓 as 51/2
multiply powers of 5 by
adding exponents
express the outer √
using an exponent of ½
multiply the outer
exponent times the inner
exponent
Ex. Simplify:
𝟑
√𝟑√𝟑
Lesson 47: More Roots Containing Roots,
Converting Rates
Ex. Simplify:
√25√5
write 25 as 52
write the inner √𝟓 as 51/2
multiply powers of 5 by
adding exponents
express the outer √
using an exponent of ½
multiply the outer
exponent times the inner
exponent
Ex. Simplify:
3
√9 4√3
When converting rates, they may be expressed as
fractions. Such as 60 mph =
𝟔𝟎 𝒎𝒊𝒍𝒆𝒔
𝟏 𝒉𝒐𝒖𝒓
The “per” is the fraction bar.
To convert a rate, simply use unit multipliers to
convert the time component (if necessary) and
then multiply by more unit multipliers to convert
the length component (if necessary).
Ex. Convert 60 miles per hour to inches per
minute.
Ex. Convert 10 miles per second to feet per hour.
Lesson 48: An Introduction to Equations
Containing Radicals
Ex. Solve:
√𝒎 + 𝟑 − 𝟓 = −𝟐
isolate the radical
square both sides of
the equation
solve
a check is required
Note: You cannot square an equation in “pieces.”
ex.
2 + 3 = 5 is true
but
22 + 32 ≠ 52
4 + 9 ≠ 25
Ex. Solve:
√𝒙 + 𝟏𝟎 + 𝟑 = −𝟏𝟐
Ex. Solve:
√𝒙𝟐 − 𝟒𝒙 − 𝟖 + 𝟒 = 𝒙
Ex. Solve:
√𝒂 + 𝟏𝟎 + 𝟐 = −𝟐
Lesson 49: Finding the y Intercept of a Line
Ex. Find the equation of the line:
find two points on the line
use them to find the line’s
slope
use one point and m in
y = mx + b to calculate b
Ex. Find the equation of the line.
Lesson 50: Completing the Square to Solve
Quadratic Equations, an Introduction
Recall:
Solve: x2 – 5x + 6 = 0
(x – 3)(x – 2) = 0
x – 3 = 0 or x – 2 = 0
x=3
or x = 2
Also, Solve: (x – 3)2 = 11
√(𝒙 − 𝟑)𝟐 = ±√𝟏𝟏
𝒙 − 𝟑 = ±√𝟏𝟏
𝒙 = 𝟑 ± √𝟏𝟏
Completing the square enables us to solve nonfactorable quadratic equations of the first form by
putting them into the second form.
Ex. Solve by completing the square:
x2 + 6x - 8 = 0
need the constant on
the other side
write out binomials
(x + k)(x + k) (where k is
½ times the x coefficient)
and add k2 to the right
take the square root of both
sides
solve for x
Ex. Solve:
x2 = 7x + 9
Ex. Solve:
-6x – 12 + x2 = 0
Lesson 51: Non-real Numbers
Consider: √𝟒 = 2 because 2∙2 = 4
What should √−𝟒 equal?
-2(-2) ≠ -4
2(2) ≠ -4
0(0) ≠ -4
There is no real number whose square = -4.
Def: √−𝟏 = 𝒊
𝑖 2 = −1
Ex. √−𝟒 = √𝟒√−𝟏 = 𝟐𝒊
Ex. √−𝟗 = √𝟗√−𝟏 = 𝟑𝒊
Ex. √−𝟏𝟓 = √𝟏𝟓√−𝟏 = √𝟏𝟓𝒊
Any number that can be written in the form a + bi
where a and b are real numbers is a complex
number.
Ex. Simplify:
3iii + 5ii - 7i – 2 + √−𝟐
write √−𝟐 as √𝟐𝒊
each i2 = -1
combine like terms
Ex. Simplify:
5i3 – 2i5 + 4i – 8 + √−𝟒
Ex. Simplify:
-5i4 + 3iii – 6 + 3i - √−𝟗
Lesson 52: Chemical Mixture Problems In Which
the Final Quantity is Known
M
C
final volume
M + C = Final Volume
%M + %C = %∙Final Volume
Ex. Christy needs 600 ml of 70% witch hazel. She
has only a 60% witch hazel solution on hand and
the drug store only sells a 90% witch hazel
mixture. How many ml of 60% witch hazel and 90%
witch hazel should Christy mix?
Ex. The chef needs to mix up 12 cups of a 50%
brine solution. He has only 40% brine solution
and 80% brine solution on hand. How much of
each should he combine?
Lesson 53: Converting Metric Units
Recall:
2.54 cm = 1 in.
100 cm = 1 m
1000 m = 1 km
Ex. Convert 2.3 square kilometers to square
inches.
Ex. Convert 3 cubic meters to cubic feet.
Lesson 55: Advanced Abstract Equations, Word
Problems Containing Quadratic Equations
Ex. Solve for b:
𝟐+
𝟑
𝒙
= 𝒚𝒛 +
𝒂+𝒚
𝒃
multiply both sides of the
equation by the LCD to cancel
the denominators
distribute ( )
isolate “b” terms on one side
factor “b” off
divide out “b’s” coefficient
Ex. Solve for m:
𝒂
𝒎
+
𝟐
𝒙+𝒚
=𝒌
Ex. Find e:
𝒄
𝒙+𝒚
−
𝟓
𝒆
=𝒋
Word Problems Containing Quadratic Equations:
Ex. Find three consecutive integers such that the
product of the first and the third is 23 more than
ten times the opposite of the second.
Ex. Find 3 consecutive even integers such that the
product of the first times the second is 10 more
than 5 times the opposite of the sum of the second
and third.
Lesson 58: Completing the Square With an x2
Coefficient Other Than 1
Ex. Solve by completing the square:
3x2 + 6x - 8 = 0
divide both sides of the
equation by 3
need the constant on
the other side
write out binomials
(x + k)(x + k) (where k is
½ times the x coefficient)
and add k2 to the right
take the square root of both
sides
solve for x
Ex. Solve by completing the square:
10x2 = -6x + 3
Ex. Solve by completing the square:
6 - 4x2 = 7x
Lesson 59: Solving Systems of Equations
Containing Fractions or Decimals
Multiply each equation so that it no longer
contains fractions or decimals. Then solve using
substitution or elimination.
Ex. Solve:
𝟏
𝟓
𝒙+
𝟏
𝟐
𝒚=
𝟕
𝟓
0.01x - 0.04y = -0.19
Ex. Solve:
5x – 0.7y = 3.6
𝟏
𝟏
𝟒
𝟑
− 𝒙+
𝒚=
𝟓
𝟏𝟐
Lesson 60: Introduction to Variation
A varies directly as B means that A = kB
thus as A increases, B increases
as A decreases, B decreases
A varies inversely as B means that A = k
thus as A increases, B decreases
as A decreases, B increases
k is a number, called the constant of
proportionality.
𝟏
𝑩
Ex. The pressure of an ideal gas varied inversely
with its volume. If four liters of the gas had a
pressure of 100 newtons per square meter, what
would be the pressure of five liters of the gas?
Ex. The mother’s consumption of chocolates
varied directly as the number of children with her
in the car. If 2 children resulted in her eating 14
chocolates, how many chocolates would she eat if
5 children were in the car?
Ex. The pressure of an ideal gas varied inversely
with its volume. If 48 liters of the gas had a
pressure of 7 atmospheres, what would be the
pressure of 56 liters of the gas?
Lesson 61: Chemical Mixture Problems in Which
the Initial Volume is Known
Initial Volume ±
X = (Initial Volume ± X)
%Initial Volume ± %X = %(Initial Volume ± X)
% of chemical of interest
Ex. The 200 lbs of 20% nitrogen fertilizer mix was
too rich for the soil. How much of the 7% nitrogen
fertilizer mix should be added to achieve a mix
containing 15% nitrogen?
Ex. Jim made 32 cups of lemonade. It was too
sour as it contained only 4% sugar. How much
sugar should Jim add to make the lemonade 25%
sugar?
Ex. The 100 gallons of brine solution was not
concentrated enough as it contained 37% water.
How many gallons of water should be evaporated
until the mixture contains just 10% water?
Lesson 62: Non-real Solutions When Completing
the Square
Ex. Solve by completing the square:
3x2 + 6x + 8 = 0
divide both sides of the
equation by 3
need the constant on
the other side
write out binomials
(x + k)(x + k) (where k is
½ times the x coefficient)
and add k2 to the right
take the square root of both
sides
solve for x
Ex. Solve:
2x2 + 10 = 3x
Lesson 64: More Complex Fractions, More
Complex Numbers
Complex Fractions:
Ex. Simplify:
𝒄+
𝟐
𝟏
+ 𝟑𝒃
𝒎
need LCD to add
denominator fractions
invert and multiply
need LCD to add C to the
fraction
Ex. Simplify:
𝒎
𝒙
+
𝟓
𝟑+
𝟐𝒃
𝒙
Complex Numbers:
Recall: √𝟐√𝟐 = 𝟐
Also, √−𝟐√−𝟐 = −𝟐
Be careful, √−𝟑√−𝟐 = √𝟑𝒊√𝟐𝒊 = √𝟔𝒊𝟐 = −√𝟔
√−𝟑√−𝟐 ≠ √𝟔
Ex. Simplify:
5iii – 4i4 + 3i – 7 + √−𝟐√−𝟓
write i4 as iiii, write
√−𝟐 = √𝟐𝒊, √−𝟓 = √𝟓𝒊
each i2 = -1
simplify & combine
like terms
Ex. Simplify:
(3i – 2)(4i + 1)
distribute
each i2 = -1
simplify & combine
like terms
Lesson 65: Advanced Substitution
Decide which Rate x Time to substitute into.
Completely replace that rate and time. Distribute.
The other Rate x Time appears. Replace that with
its numeric value.
Ex. Solve:
RATA = 90, RBTB = 360, RB = 3RA, TA + TB = 14
Ex. Solve:
RATA = 105, RBTB = 30, RA = 5RB, TA + TB = 17
Lesson 66: LCD Which Contain Opposite Factors
𝟑
−𝟑
𝟕
𝟕
Consider: − =
=
𝟑
−𝟕
Ex. Add:
𝟐
𝒎−𝟑
−
𝒑
−𝒎+𝟑
need LCD for both
rational expressions
multiply the numerator
& denominator of one
fraction by -1
add,
don’t lose the
denominator
Ex. Add
𝟒𝒂−𝟑
−𝒂−𝟐
−
𝒂−𝟓
𝒂+𝟐
Lesson 67: Rationalizing Denominators
Containing Sums
Recall:
Conjugates are the same two terms with
opposite signs in the middle:
Ex.
2x + 3, 2x – 3
𝟐√𝟓 − 𝟑, 𝟐√𝟓 + 𝟑
-√𝟑 + 𝟏, −√𝟑 − 𝟏
The product of conjugates is special:
(2x + 3)(2x – 3) = 4x2 – 6x + 6x – 9 = 4x2 – 9
(2√𝟓 - 3) (2√𝟓 + 3) = 4∙5 + 6√𝟓 - 6√𝟓 - 9 = 11
(-√𝟑 + 1) (-√𝟑 - 1) = 3 + √𝟑 - √𝟑 - 1 = 2
The product of conjugates is the difference of
squares.
Ex. Simplify:
𝟐
−𝟒+ √𝟓
multiply the numerator
and the denominator
by the conjugate of the
denominator
Ex. Simplify:
𝟓
𝟐√𝟓 − 𝟑√𝟔
Ex. Simplify:
1
-2√3 – √7
Lesson 68: Using Your Calculator to Find nth Roots
It is not necessary in this class to have a
calculator that can find nth roots. However, if you
think your calculator will do so, this lesson helps
you figure out how.
Method 1:
4
1
Recall: √81= 81 ⁄4
Enter in your calculator:
81 ^ (1/4)
The result should be 3
Method 2:
𝒏
Find the √𝒙 key on your calculator. You may
need to press a 2nd key first to access it.
Enter in your calculator:
𝒏
4 √𝒙 81
The result should be 3
If the result is not 3, try:
𝒏
81 √𝒙 4
If none of these methods work and you think your
calculator can find nth roots, please see me after
class.
Lesson 70: Abstract Equations With Parenthesis
Ex. Solve for a:
𝒒
𝒓
= 𝒎(
𝟑
𝒂+𝒃
𝟐
− )
𝒑
distribute m
multiply both sides of the
equation by the LCD to cancel
the denominators
distribute ( )
isolate “a” terms on one side
factor “a” off
divide out “a’s” coefficient
Ex. Solve for x:
𝒗
𝒙
+ 𝒚 = 𝒌 (𝟐 +
𝒚
𝒋+𝟓
)
Ex. Find k:
𝒓 = 𝒒(
𝒋
𝒙−𝒌
𝒎
+ )
𝟐
Lesson 71: The Quadratic Formula
Derive the quadratic formula by completing the
square to solve:
ax2 + bx + c = 0
divide both sides of the
equation by a
need the constant on
the other side
write out binomials
(x + k)(x + k) (where k is
½ times the x coefficient)
and add k2 to the right
need LCD to add fractions
take the square root of both
sides
solve for x
Memorize: 𝒙 =
−𝒃 ±√𝒃𝟐 − 𝟒𝒂𝒄
𝟐𝒂
Round and round the mulberry bush
“x is equal to negative b”
The monkey chased the weasel
“Plus or minus the square root”
The monkey stopped to pull up his socks
“of b squared minus 4 a c”
Pop goes the weasel
“All over 2 a”
Ex. Use the quadratic formula to solve:
3x2 – 4 = 5x
Ex. Solve using the quadratic formula:
2x2 - 7x = 3
Lesson 73: Rationalizing the Denominator When
the Numerator is a Sum
Ex. Simplify:
𝟑−𝟓√𝟐
𝟕√𝟐
multiply the numerator
and the denominator
by √𝟐
simplify
Ex. Simplify
𝟓√𝟐− 𝟒√𝟏𝟐
𝟑√𝟐 + 𝟖√𝟑
multiply the numerator
and denominator by
the conjugate of the
denominator
simplify each term
combine like terms
factor and reduce if
possible, do not cancel
part of a sum
Ex. Simplify
√𝟐𝟒 + 𝟓√𝟐
𝟕√𝟐 − 𝟑√𝟑
Lesson 74: Uniform Motion Problems in Which
Both Distances are Known
Ex. Rachel lived farther from her parents than her
brother Derek. In fact, she had to drive 360 miles
to get to their parents’ home. Derek decided to
bicycle the 45 miles to his parents’ home. Even
though Rachel drove four times as fast as Derek
bicycled, it still took her three hours longer to get
home than it took Derek. What were the rates and
times of each of them?
Ex. Brenda was traveling twice as fast as
Gwendolyn. That’s why she could cover 66 miles
in just 4 hours more than it took Gwendolyn to
cover 21 miles. What were the rates and times of
each?
Lesson 75: Factorable Denominators With
Opposite Factors
Ex. Add:
𝒙+𝟑
𝒙𝟐 + 𝟒𝒙−𝟓
−
𝒙−𝟒
𝟏−𝒙
factor the denominator
multiply the numerator
and the denominator
of the 2nd fraction by -1
need the LCD for each
add
Ex. Add:
𝒙−𝟏
𝒙𝟐 + 𝟐𝒙 −𝟖
+
𝒙+𝟑
𝟐−𝒙
Ex. Add:
−𝟑
𝒙𝟐 − 𝒙−𝟐𝟎
−
𝒙−𝟐
𝟓−𝒙
Lesson 76: Solving Three Equations and Three
Variables Using Substitution and Elimination
We need the (x, y, z) that makes all three equations
true.
First use substitution. Substitute for the same
variable in two different equations. This makes
two equations with the same two variables. Solve
them using substitution or elimination. Find the
last variable’s value.
Ex. Solve:
2x + 3y – z = 0
x+y+z=2
x + 2y = 0
Ex. Solve:
x – y + z = -7
2x + 3y – z = 0
y = 3z
Lesson 77: Advanced Equations Containing
Radicals
Ex. Solve:
𝟑
√𝒙𝟑 + 𝟗𝒙𝟐 + 𝟒𝒙 + 𝟒 − 𝟑 = 𝒙
isolate the root
cube both sides
solve
Ex. Solve:
√𝒙 + 𝟏𝟐 + √𝒙 = 𝟔
need one root per side
square both sides,
use FOIL on the right
isolate remaining root
square both sides
a check is required
when you square both
sides of an equation
Ex. Solve:
√𝒀 − 𝟗 − 𝟑 = √𝒀
Lesson 79: Metric Volume
Recall: units of length can be used to measure
areas when squared or volumes when cubed:
1 cm2
1 cm
1 cm
1 cm3 = 1 ml
1000 ml = 1 liter
1000 cm3 = 1 liter
1 cm3
1 cm
1 cm
1 cm
Ex. Use unit multipliers to convert 8 cubic feet to
liters
Ex. Use unit multipliers to convert 9000 ml to
cubic inches.
Lesson 80: Using Proportions to Solve Variation
Problems
Recall:
A varies directly as B means A = kB or
A varies inversely as B means A = k
𝟏
𝑩
𝐴1
𝐴2
or
=
𝐴1
𝐴2
𝐵1
𝐵2
=
𝐵2
𝐵1
Ex. The number of worker bees in the hive varied
directly as the number of drones. If 15 worker
bees were present when there were 2 drones, how
many worker bees were there when 1300 drones
were present?
Ex. The illumination value of the lamp varied
inversely as the square of the distance from the
lamp. If the illumination value of the lamp was 25
at a distance of 2 feet from the lamp, what was the
illumination value of the lamp at a distance of 10
feet from the lamp?
Ex. The mouse population varied inversely as the
square of the cat population. If there were 12
mice present when there were 6 cats, how many
mice were there when 12 cats were present?
Lesson 81: Division of Complex Numbers
Do not leave i in the denominator.
Ex. Simplify:
𝟐+𝟑𝒊
𝟕−𝟐𝒊
multiply the numerator and the
denominator by the conjugate of
the denominator
i2 = -1
write as a sum of two fractions
reduce if possible
Ex. Simplify:
−𝟐𝒊 +𝟓
𝟑 −𝟒𝒊
Ex. Simplify:
𝟐 +𝟓𝒊
−𝟑𝒊 + 𝟓
Lesson 82: Advanced Complex Fractions
Ex. Simplify:
𝟑
𝟏+
𝒎
𝟐−
𝒙
𝒚
get a LCD and add
𝒙
2-𝒚
invert and multiply
get a LCD and add
invert and multiply
Ex. Simplify:
𝒂
𝟑+
𝒙
𝒌−
𝒋
𝒎
Ex. Simplify:
𝒙
𝒂−
𝒃
𝒄+
𝟐
𝒌
Lesson 83: Exponents Which are Variables
Recall:
x2x3 = x5
𝒙𝟓
𝒙𝟐
= 𝒙𝟑
add exponents to multiply powers of x
subtract exponents to divide powers of x
(x2)3 = x6 multiply the exponents
Ex. Simplify:
𝒙⁄ 𝒚 𝟑𝒙 𝒚⁄
𝒂 𝟐𝒃 𝒂 𝒃 𝟓
add exponents to multiply
fractions need the LCD to
add
Ex. Simplify:
𝒃
𝒙𝟐𝒂 𝒚 ⁄𝟑
𝒙−𝒂+𝟑 𝒚𝒃
subtract exponents to divide
Ex. Simplify:
(𝒙𝒎 )𝟑 𝒚𝒙+𝟐
𝒙𝟐𝒎
Lesson 84: Consistent, Dependent Systems
Consider:
Consistent: At least one solution
Inconsistent: No solution
Dependent: One equation is a multiple of the
other, else independent.
What does the algebra look like if you solve an
inconsistent (no solution) system?
Consider: Solve y = 2x + 6
y = 2x - 3
What does the algebra look like if you solve a
dependent (same line) system?
consider: Solve 2x + y = 3
4x + 2y = 6
Ex. Is the following system of equations
consistent or inconsistent, dependent or
independent?
2x – 3y = 5
6y = 4x – 48
Lesson 85: One Type of Nonlinear System of
Equations
Ex. Solve:
BTD – 8TD = 64
BTD + 8TD = 32
use elimination to find BTD
now find TD
now find B
Ex. Solve:
BTD + 7TD = 77
BTD - 7TD = 49
Lesson 86: Introduction to Inequalities
Consider the number line:
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Numbers are larger as you go to the right.
Ex. 4 > 2 because 4 lies to the right of 2
Ex. -2 > -4 because -2 lies to the right of -4
(Remember the arrow points at the smaller value.)
Consider:
means
means
<
>
<
>
means
means
≥
≤
Domain:
The domain consists of the allowable x values.
D = {integers} means your answer must consist
only of integers, …-3, -2, -1, 0, 1, 2, 3…
D = {reals} means your answer may be any real
number (any number on the number line)
Ex. Graph x > 2, D = {integers}
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
2
3
4
5
6
Ex. Graph x > 2, D = {reals}
-6
-5
-4
-3
-2
-1
0
1
When multiplying or dividing both sides of an
inequality by a negative value, flip the inequality
symbol.
Ex. Graph: -x > 7; D = {reals}
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Ex. Graph –x -5; D = {positive integers}
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Lesson 87: The Slope Formula
Recall: slope = m =
𝒓𝒊𝒔𝒆
𝒓𝒖𝒏
=
𝒖𝒑
𝒓𝒊𝒈𝒉𝒕
= −
𝒅𝒐𝒘𝒏
𝒓𝒊𝒈𝒉𝒕
Ex. Find the slope of the line passing through
(-3, 4) and (2, -5).
memorize: m =
𝒚𝟐 − 𝒚𝟏
𝒙𝟐 − 𝒙𝟏
Ex. Find the slope of the line passing through
(2, -4) and (-6, 5).
Lesson 88: The Distance Formula
Recall: Find the distance between
(-3, 4) and (2, -5).
memorize: d = √(𝒙𝟐 − 𝒙𝟏 )𝟐 + (𝒚𝟐 − 𝒚𝟏 )𝟐
Ex. Find the distance between
(2, -4) and (-6, 5).
Lesson 89: Compound Inequalities
“And” means both conditions must be met to be
included in the answer.
“Or” means include any number which satisfies
either condition.
Ex. Graph
-6
-5
-4
-3
-2
-1
0
1
2
3
4
-4 > -x -2 and x + 3 ≥ 4, D = {reals}
5
6
Ex. Graph
-6
-5
-4
-3
-2
-1
0
1
2
3
4
-x - 3 < -2 or x + 3 ≤ 5 , D = {integers}
5
6
Ex. Graph
-6
-5
-4
-3
-2
-1
0
-5 ≤ -x - 3 < -2 , D = {reals}
1
2
3
4
5
6
Ex. Graph
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
-x - 3 < -2 or -7 > -5 + x, D = {integers}
6