Download Systems of Linear Equations and Matrices

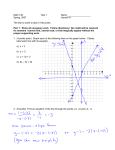
Systems of Linear Equations and Matrices
1. Systems of Linear Equations in
2
and
3 variables:
Simultaneous Equations: One often first meets
Augmented Matrix:
matrices when solving a pair of linear equations like
ax + by =
r
cx + dy =
s
If the coefficients of the variables
[
r
]
s
associated with this system of linear equations. This
x, y in the equations
matrix is sometimes written
[
are written as rows with entries aligned so that a column
consists of the coefficients of an individual variable we
obtain a
a b
c d
2 × 3 matrix by adding the 'right hand values'
as a third column to form the so-called
a b
c d
| r
]
| s
to emphasize the position of the
= sign.
One huge advantage of introducing the augmented matrix is that it converts a system of linear equations into something a
computer can understand, and this in turn allows algorithms to be developed for determing solutions of simultaneous
equations. Recall how you might have done this in the past.
A standard method for determining
eliminate one variable, say
equation: subtract
x
and
y is to
x, from the second
c/a times the first equation from
the second equation we obtain a new pair of equations
ax + by = r,
cx + dy −
c
cr
(ax + by) = s −
,
a
a
which after simplification becomes
ax + by
=
1
0x + a (ad − bc)y =
1
(as
a
r
.
− cr)
x, it now follows immediately that
y = (as − cr)/(ad − bc), while x can be found by
substituting back for y in the first equation:
and solving for
x =
x
as − cr
) = r,
ad − bc
to discover that
rd − bs
,
ad − bc
y =
(c/a)Row 1 from Row 2 to create a new Row 2, while
leaving Row 1 unchanged:
[
a b
c d
a
r R2 − ca R1
] −−−−−→ [
0
s
b
− bc)
1
(ad
a
1
(as
a
r
].
− cr)
But this is simply the augmented matrix associated with
Having eliminated
ax + b(
In augmented matrix terms we first subtracted
the linear system immediately to the left. Crucially, the
solution set
x =
rd − bs
,
ad − bc
y =
as − cr
,
ad − bc
of the original system
remained the same after these row operations on
the augmented matrix,
can be easily read off by evaluation and back
as − cr
.
ad − bc
substitution once the augmented matrix is in echelon
(step) form.
Let's look at another system to see what additional operations might be performed on rows without changing the solution
set of the system:
Solve for
x, y and z in the system
Now as before we can successively add/subtract
y+z
=
3x + 6y − 3z =
−2x − 3y + 7z =
multiples of one row to another to introduce 0 entries:
4,
3,
10 .
R +2 R
3
1
−−−−
→
The associated augmented matrix is
1
⎡ 0
A =
3
6
⎣ −2 −3
4 ⎤
3
10 ⎦
1
−3
7
Since the first entry in the first row of
R −R
2
−−3−−→
A is 0, interchange
R ↔R
6
⎡ 3
0
1
⎣ −2 −3
−3
1
7
3 ⎤
4 .
10 ⎦
To simplify calculations mutiply the new Row 1 by
2
⎡ 1
−−−−−−→
0
1
⎣ −2 −3
1
3
R1 → R1
−1
1
7
1⎤
4 ,
8⎦
−1
1
4
x + 2y − z =
y+z =
4z =
1,
4,
8.
Since interchanging equations and multiplying an
1/3:
1 ⎤
4 .
10 ⎦
2. General Systems of Linear Equations:
⎡1 2
0 1
⎣0 0
1 ⎤
4
12 ⎦
−1
1
5
which is the augmented matrix associated with
Row 1 and Row 2:
2
A −−1−−−→
⎡1 2
0 1
⎣0 1
equation by a non-zero constant does not affect the
solutions of an equation, the solution set of this last
system is the same as the solution set of the original
z = 2, and hence
by back substitution that y = 2, x = −1 .
system. We thus see immediately that
the algorithm just formulated for solving low-dimensional systems of linear
equations by reducing the augmented matrix to 'stepped form' applies quite generally. It is usually known as Gaussian
Elimination because of its use by Gauss in the early 19th century, though it was known many years earlier to the Chinese. By
a system of
m
linear equations in
where coefficients
s1 , s2 , … , sn
s1 , s2 , … , sn
ajk
n variables we mean the set of equations:
a11 x1 + a12 x2 + ⋯ + a1n xn
a21 x1 + a22 x2 + ⋯ + a2n xn
=
=
b1
b2
⋮
am1 x1 + am2 x2 + ⋯ + amn xn
⋮
=
⋮
bm
and 'right hand values' bj can be real or complex. A solution for such a system consists of
such that each equation holds true when
n values
x1 = s1 , x2 = s2 , … , xn = sn ; the set of all possible values
is called the Solution Set of the system. Two systems of linear equations are said to be Equivalent when
they have the same solution set.
Fundamental Questions for a general system of linear equations:
Is the system CONSISTENT, i.e., does there exist at least one solution?
If a solution exists, is it the only one, i.e is it UNIQUE ?
If no solution exists, i.e., the solution set is empty, we say the system is INCONSISTENT.
In the previous simple examples involving only 2 or 3 variables there was always a solution and it was unique in the sense
that there was only one choice of solutions. But that's not always the case. When
because the graph of a pair of linear equations in
2 variables is a pair 2
m = n = 2
this can be seen graphically
straight lines in the plane, and the solution set
consists of the points of intersection of the lines. The various possibilities are shown in:
The first system is consistent with unique solutions. In the second and third examples, however, the lines are parallel, so
the solution set will be empty - hence the system inconsistent - when the parallel lines are distinct as in the second example,
while the system will be consistent but have infintely many solutions when the parallel lines coincide as in the third case.
Since the graph of a linear equation in
3
variables is a plane in
3-space, can you see what could happen for 3 equations in 3
variables?
Going beyond
3
variables, however, requires algebra. To each general system of
m linear equations in n variables we can
associate naturally two matrices, thinking of a matrix as an arrary of numbers:
1. Coefficient matrix: the coefficients are written
2. Augmented matrix: add the column of right
as rows with entries aligned so that a column
hand values to the
consists of the coefficients of an individual variable:
matrix:
⎡ a11
a21
⎢
⎢
⎢
⎢ ⋮
⎣a
m1
making an
a12
a22
a13
a23
⋮
⋮
am2
am3
a1n ⎤
a2n ⎥
⎥
⎥
⋯
⋮ ⎥
⋯ amn ⎦
⎡ a11
a21
⎢
⎢
⎢
⎢ ⋮
⎣a
m1
⋯
⋯
m × n matrix.
making an
n columns of the coefficient
a12
a22
a13
a23
⋯
⋯
⋮
am2
⋮
am3
⋯
⋮
⋯ amn
a1n
a2n
b1 ⎤
b2 ⎥
⎥
⎥
⋮ ⎥
b ⎦
m
m × (n + 1) matrix.
The same operations as before, now called Elementary Row operations, also can be carried out on the rows of such
matrices. Formally,
Elementary Row Operations on a matrix:
(Replacement) replace one row by the sum of itself and a multiple of another row,
(Interchange) interchange two rows,
(Scaling) multiply all entries in a row by a non-zero constant.
Notice that elementary row operations can be applied to any matrix. We shall say that matrices
A, B are Row Equivalent,
A ∼ B, when there is a sequence of elementary row operations that takes A into B. For later purposes, note also
that elementary row operations are reversible, so if A ∼ B, then B ∼ A.
and write
But the crucial point of the discussion in
[
a
0
2
and
3 variables carries over to general systems: the earlier examples of
⎡1 2
0 1
⎣0 0
r
],
1
(as
− cr)
a
b
1
(ad
− bc)
a
−1
1
4
1⎤
4
8⎦
suggest the following:
Definition: a matrix is said to be in Echelon Form if
all non-zero rows lie above any rows of all zeros,
the leading entry of a row lies in a column to the right of the
leading entry in the row above it,
only zero entries lie in a column below the leading entry of a row.
A typical structure for a general matrix in Row Echeon Form is thus
⎡⊛
0
⎢
⎢0
⎢
⎢
⎢
0
⎢
⎢0
⎣0
∗
0
0
0
0
0
∗
⊛
0
0
0
0
∗
∗
⊛
0
0
0
∗
∗
∗
0
0
0
∗
∗
∗
⊛
0
0
∗
∗
∗
∗
0
0
⋯
⋯
⋯
⋯
⋯
⋯
∗⎤
∗⎥
∗⎥
⎥
⎥
∗⎥
⎥
0⎥
0⎦
⊛ entries are the non-zero leading entries, often called pivots, in a row and the ∗ entries that follow a pivot in a
row can be zero or non-zero. Columns in which a pivot ⊛ occurs are often called pivot columns. In practice, it will almost
where the
never happen that all the entries in the first columns are zero, but entire rows of zeros often happen as we shall soon see.
The terms pivot and pivot column are used because in the earlier examples of linear systems the pivots and pivot columns
are what we used to row reduce the augmented matrix to echelon form (we "pivoted around them").
Your Turn Now: consider the three systems previously described graphically:
I:
x−y = 0
x − 2y + 2 = 0
II:
x − y = −2
x−y = 2
III:
x−y = 0
2x − 2y = 0
Problem I : Compute the augmented matrix and echelon form for each system. Use the echelon form to find the
solution set.
Problem II : How do the echelon forms differ? How does the echelon form differ between consistent and inconsistent
systems?
Problem III : In each case, how many pivot columns are there? How does the number and position of the pivot
column depend on the answers to the Fundamental Questions?